2.4 线段的垂直平分线 课件(共23张PPT) 湘教版数学八年级上册
文档属性
| 名称 | 2.4 线段的垂直平分线 课件(共23张PPT) 湘教版数学八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
2.4 线段的垂直平分线
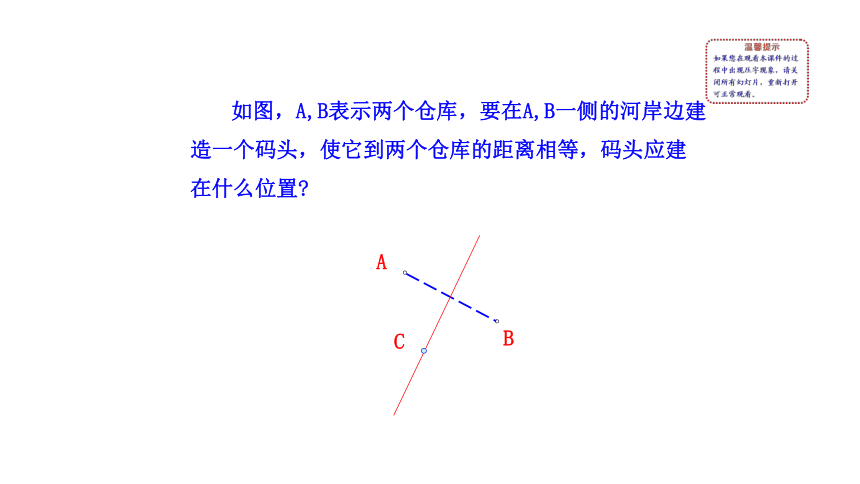
如图,A,B表示两个仓库,要在A,B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置
A
B
C
如果一个图形沿某一条直线 ,两旁的图形能够 ,这个图形就是轴对称图形.
这条直线叫作_________.
对称轴
对折
完全重合
温故知新
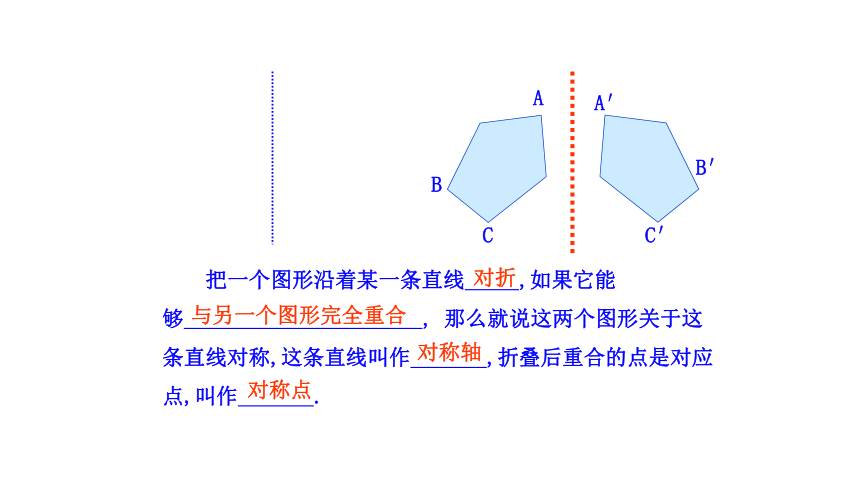
把一个图形沿着某一条直线 ,如果它能够 , 那么就说这两个图形关于这
条直线对称,这条直线叫作_______,折叠后重合的点是对应
点,叫作 .
A′
A
B
C
B′
C′
对折
与另一个图形完全重合
对称点
对称轴
已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?
C的对称点是_____
____的对称点是E
D
A的对称点是F
图中的对称点有哪些
B
1、经历探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念;
2、探索并了解线段的垂直平分线的相关性质.
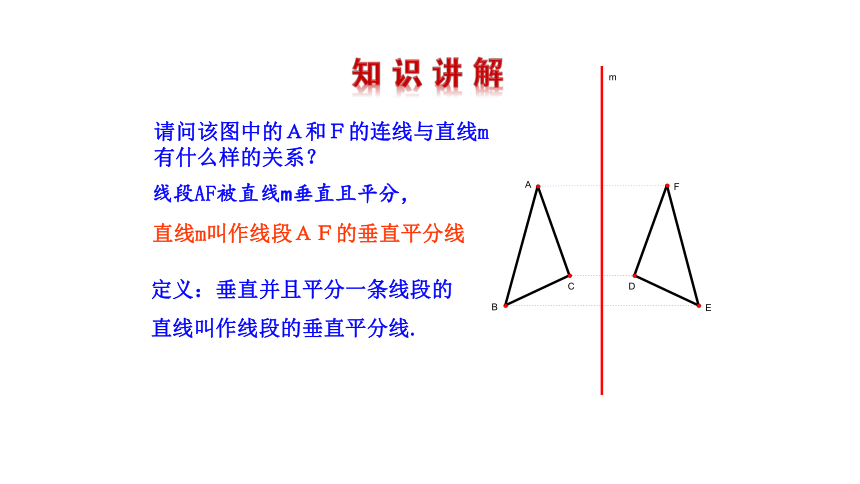
线段AF被直线m垂直且平分,
直线m叫作线段AF的垂直平分线
定义:垂直并且平分一条线段的直线叫作线段的垂直平分线.
请问该图中的A和F的连线与直线m
有什么样的关系?
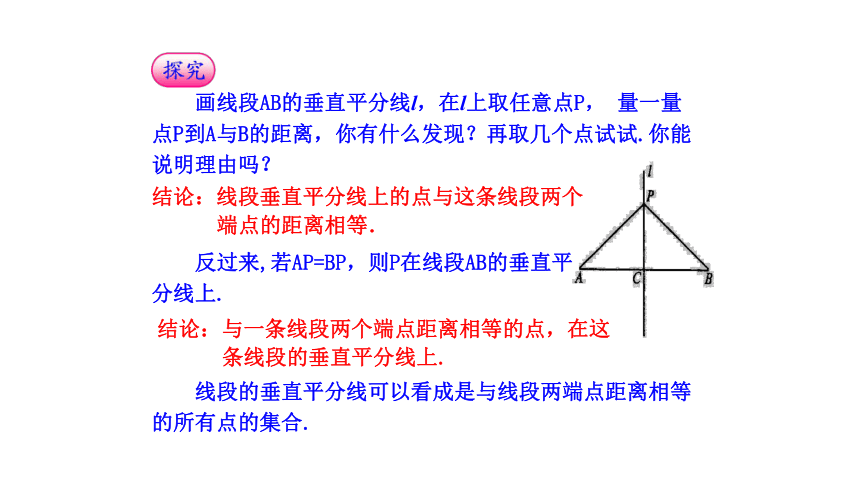
画线段AB的垂直平分线l,在l上取任意点P,量一量点P到A与B的距离,你有什么发现?再取几个点试试.你能说明理由吗?
结论:线段垂直平分线上的点与这条线段两个
端点的距离相等.
反过来,若AP=BP,则P在线段AB的垂直平
分线上.
结论:与一条线段两个端点距离相等的点,在这
条线段的垂直平分线上.
线段的垂直平分线可以看成是与线段两端点距离相等的所有点的集合.
如何作出线段的垂直平分线?
由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端点距离相等的两点并连接即可.
作线段的垂直平分线.
已知:线段AB,
求作:线段AB的垂直平分线.
A
B
C
D
作法:
(2)作直线CD.
CD即为所求.
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点;
【例题1】
B
【跟踪训练】
B
【例题2】
【答案】A
【跟踪训练】
3
作
作
1.【广西梧州中考】如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是 ( )
A.12 B.13
C.14 D.15
B
2.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,
则∠BDC= ( )
A.50°
B.100°
C.120°
D.130°
B
3.下列尺规作图,能判断AD是△ABC的BC边上的高的是 ( )
B
4.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C的度数为 ( )
A.21°
B.30°
C.24°
D.40°
C
5.如图,在△ABC中,已知点O是边AB,AC垂直平分线的交点,点E是∠ABC,∠ACB角平分线的交点,若∠BOC+∠BEC=180°,则∠BAC=______°.
36
6.如图,在△ABC中,AD为∠BAC的平分线,AD的垂直平分线EF交BC的延长线于点F,连接AF.求证:∠FAC=∠B.
证明:∵EF垂直平分AD,∴FD=FA,∴∠FAD=∠FDA.又∵∠FAC+∠CAD=∠FAD,∠FDA=∠B+∠BAD,∴∠FAC+∠CAD=∠B+∠BAD.又∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FAC=∠B.
在数学的领域中,提出问题的艺术比解答问题的艺术更为重要。
——康托尔
2.4 线段的垂直平分线
如图,A,B表示两个仓库,要在A,B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置
A
B
C
如果一个图形沿某一条直线 ,两旁的图形能够 ,这个图形就是轴对称图形.
这条直线叫作_________.
对称轴
对折
完全重合
温故知新
把一个图形沿着某一条直线 ,如果它能够 , 那么就说这两个图形关于这
条直线对称,这条直线叫作_______,折叠后重合的点是对应
点,叫作 .
A′
A
B
C
B′
C′
对折
与另一个图形完全重合
对称点
对称轴
已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?
C的对称点是_____
____的对称点是E
D
A的对称点是F
图中的对称点有哪些
B
1、经历探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念;
2、探索并了解线段的垂直平分线的相关性质.
线段AF被直线m垂直且平分,
直线m叫作线段AF的垂直平分线
定义:垂直并且平分一条线段的直线叫作线段的垂直平分线.
请问该图中的A和F的连线与直线m
有什么样的关系?
画线段AB的垂直平分线l,在l上取任意点P,量一量点P到A与B的距离,你有什么发现?再取几个点试试.你能说明理由吗?
结论:线段垂直平分线上的点与这条线段两个
端点的距离相等.
反过来,若AP=BP,则P在线段AB的垂直平
分线上.
结论:与一条线段两个端点距离相等的点,在这
条线段的垂直平分线上.
线段的垂直平分线可以看成是与线段两端点距离相等的所有点的集合.
如何作出线段的垂直平分线?
由两点确定一条直线和线段垂直平分线的性质可知,只要作出到线段两端点距离相等的两点并连接即可.
作线段的垂直平分线.
已知:线段AB,
求作:线段AB的垂直平分线.
A
B
C
D
作法:
(2)作直线CD.
CD即为所求.
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点;
【例题1】
B
【跟踪训练】
B
【例题2】
【答案】A
【跟踪训练】
3
作
作
1.【广西梧州中考】如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是 ( )
A.12 B.13
C.14 D.15
B
2.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,
则∠BDC= ( )
A.50°
B.100°
C.120°
D.130°
B
3.下列尺规作图,能判断AD是△ABC的BC边上的高的是 ( )
B
4.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C的度数为 ( )
A.21°
B.30°
C.24°
D.40°
C
5.如图,在△ABC中,已知点O是边AB,AC垂直平分线的交点,点E是∠ABC,∠ACB角平分线的交点,若∠BOC+∠BEC=180°,则∠BAC=______°.
36
6.如图,在△ABC中,AD为∠BAC的平分线,AD的垂直平分线EF交BC的延长线于点F,连接AF.求证:∠FAC=∠B.
证明:∵EF垂直平分AD,∴FD=FA,∴∠FAD=∠FDA.又∵∠FAC+∠CAD=∠FAD,∠FDA=∠B+∠BAD,∴∠FAC+∠CAD=∠B+∠BAD.又∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FAC=∠B.
在数学的领域中,提出问题的艺术比解答问题的艺术更为重要。
——康托尔
同课章节目录
