2.5 全等三角形 第2课时 (共20张PPT) 湘教版数学八年级上册
文档属性
| 名称 | 2.5 全等三角形 第2课时 (共20张PPT) 湘教版数学八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 901.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 21:10:38 | ||
图片预览






文档简介
(共20张PPT)
2.5 全等三角形
第2课时
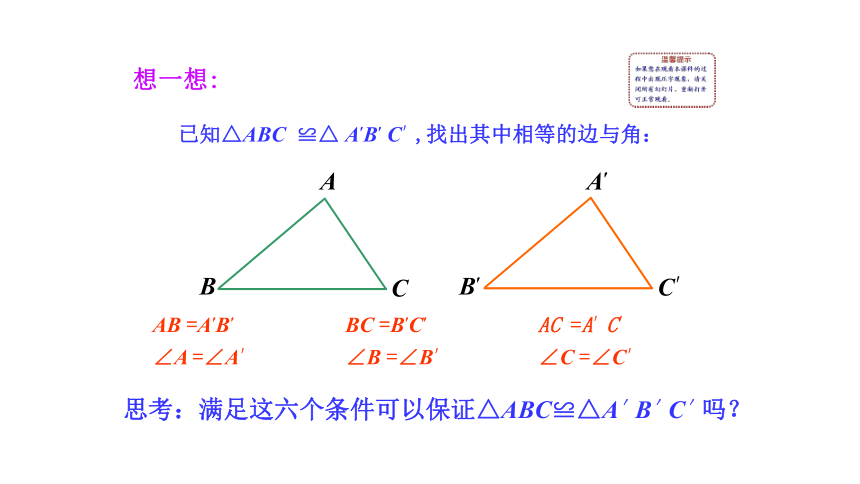
∠A =∠A′
AB =A′B′
已知△ABC ≌△ A′B′ C′,找出其中相等的边与角:
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
想一想:
A
B
C
A′
B′
C′
∠B =∠B′
BC =B′C′
∠C =∠C′
AC =A′C′
追问1 当满足一个条件时, △ABC 与△A′B′C′
全等吗?
动脑思考,分类辨析
思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗?
追问2 当满足两个条件时, △ABC 与△A′B′C′
全等吗?
① 两边
② 一边一角
③ 两角
两个条件
① 三边
② 三角
③ 两边一角
④ 两角一边
三个条件
追问3 当满足三个条件时, △ABC 与△A′B′C′全等吗?满足三个条件时,又分为几种情况呢?
1.理解判定三角形全等的“边角边”条件.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.能运用“SAS”证明简单的三角形全等问题.
做一做:先任意画出△ABC.再画一个△A′B′C′, 使A′B′=AB, A′C′=AC,∠A′=∠A.(即有两边和它们的夹角分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗
画法:
2. 在射线A′M上截取A′B′=AB;
3. 在射线A′N上截取A′C′=AC;
1. 画∠MA′N=∠A;
4. 连接B′C′,
∴△A′B′C′就是所求的三角形.
用数学语言表述:
A
B
C
D
E
F
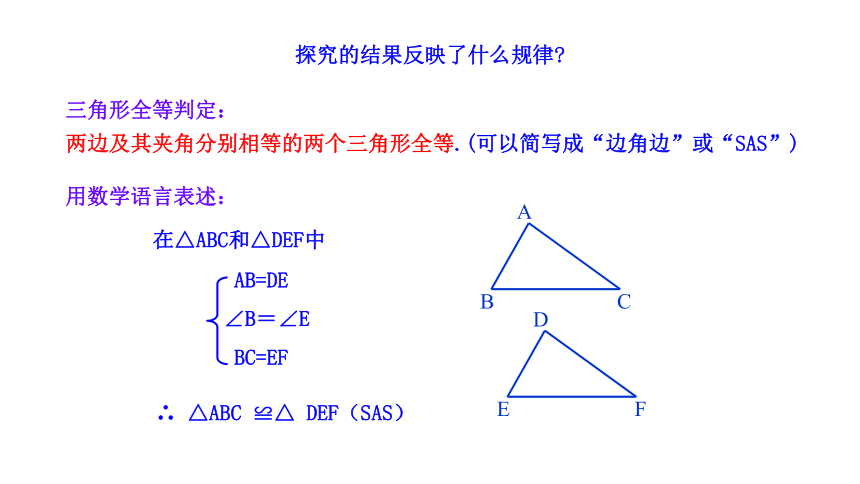
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SAS)
AB=DE
∠B=∠E
BC=EF
探究的结果反映了什么规律
三角形全等判定:
两边及其夹角分别相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
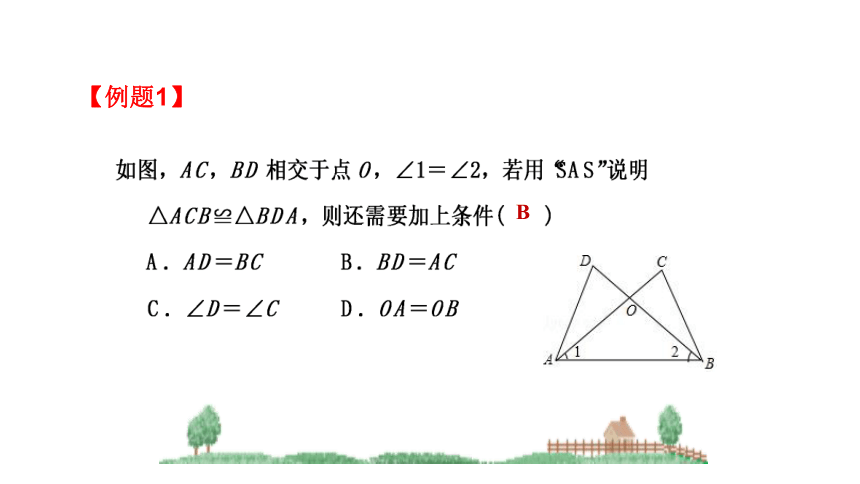
【例题1】
B
【跟踪训练】
【例题2】
①
利用SAS确定两个三角形全等
【跟踪训练】
SAS
1.下列条件中,不能确定△ABC和△A′B′C′全等的是 ( )
A.BC=B′C′,BA=B′A′,∠B=∠B′
B.∠A=∠A′,AC=A′C′,BC=B′C′
C.∠A=∠A′,AB=A′B′,AC=A′C′
D.∠C=∠C′,AC=A′C′,BC=B′C′
B
2.如图,BE=CD,AD=AE,∠1=∠2=110°,∠BAE=60°,则∠CAE等于 ( )
A.20° B.30°
C.40° D.50°
A
3.【陕西中考】如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD,求证:CF=DE.
4.如图,AD是△ABC的边BC上的中线,∠ADB,∠ADC的平分线分别交AB,AC于点E,F,连接EF,则EF,BE,CF之间的数量关系正确的是 ( )
A.BE+CF>EF
B.BE+CF≥EF
C.BE+CF<EF
D.BE+CF=EF
A
5.如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为_____.
4
6.如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
数学,科学的女皇;数论,数学的女皇。
——高斯
2.5 全等三角形
第2课时
∠A =∠A′
AB =A′B′
已知△ABC ≌△ A′B′ C′,找出其中相等的边与角:
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
想一想:
A
B
C
A′
B′
C′
∠B =∠B′
BC =B′C′
∠C =∠C′
AC =A′C′
追问1 当满足一个条件时, △ABC 与△A′B′C′
全等吗?
动脑思考,分类辨析
思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗?
追问2 当满足两个条件时, △ABC 与△A′B′C′
全等吗?
① 两边
② 一边一角
③ 两角
两个条件
① 三边
② 三角
③ 两边一角
④ 两角一边
三个条件
追问3 当满足三个条件时, △ABC 与△A′B′C′全等吗?满足三个条件时,又分为几种情况呢?
1.理解判定三角形全等的“边角边”条件.
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.能运用“SAS”证明简单的三角形全等问题.
做一做:先任意画出△ABC.再画一个△A′B′C′, 使A′B′=AB, A′C′=AC,∠A′=∠A.(即有两边和它们的夹角分别相等).把画好的△A′B′C′剪下,放到△ABC上,它们全等吗
画法:
2. 在射线A′M上截取A′B′=AB;
3. 在射线A′N上截取A′C′=AC;
1. 画∠MA′N=∠A;
4. 连接B′C′,
∴△A′B′C′就是所求的三角形.
用数学语言表述:
A
B
C
D
E
F
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SAS)
AB=DE
∠B=∠E
BC=EF
探究的结果反映了什么规律
三角形全等判定:
两边及其夹角分别相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
【例题1】
B
【跟踪训练】
【例题2】
①
利用SAS确定两个三角形全等
【跟踪训练】
SAS
1.下列条件中,不能确定△ABC和△A′B′C′全等的是 ( )
A.BC=B′C′,BA=B′A′,∠B=∠B′
B.∠A=∠A′,AC=A′C′,BC=B′C′
C.∠A=∠A′,AB=A′B′,AC=A′C′
D.∠C=∠C′,AC=A′C′,BC=B′C′
B
2.如图,BE=CD,AD=AE,∠1=∠2=110°,∠BAE=60°,则∠CAE等于 ( )
A.20° B.30°
C.40° D.50°
A
3.【陕西中考】如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD,求证:CF=DE.
4.如图,AD是△ABC的边BC上的中线,∠ADB,∠ADC的平分线分别交AB,AC于点E,F,连接EF,则EF,BE,CF之间的数量关系正确的是 ( )
A.BE+CF>EF
B.BE+CF≥EF
C.BE+CF<EF
D.BE+CF=EF
A
5.如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为_____.
4
6.如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
数学,科学的女皇;数论,数学的女皇。
——高斯
同课章节目录
