初中数学湘教版八年级上册 2.6 用尺规作三角形课件(21张PPT)
文档属性
| 名称 | 初中数学湘教版八年级上册 2.6 用尺规作三角形课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 994.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 21:53:00 | ||
图片预览








文档简介
(共21张PPT)
2.6 用尺规作三角形
方法一:度量法,先量出已知线段的长度,再画出一条和这条线段长度相等的线段.
1.如何画一条线段等于已知线段.
2.尺规作图的一般步骤:①已知;②求作;③作法;④证明.
方法二:尺规法,用直尺画一条射线,用圆规在射线上截取线段等于已知线段.
1.经历操作实践活动,会用尺规作已知三边的三角形.
2.在作图中会用规范的作图语言,写出作图步骤.
3.掌握在给出的两边及其夹角的条件下,能够利用尺规作三角形;
4.经历操作实践活动,会用尺规作已知两角及其夹边的三角形.
已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
A
B
(5)过D′作射线O′B′;
O
A
B
C
D
O′
A′
B′
D′
C′
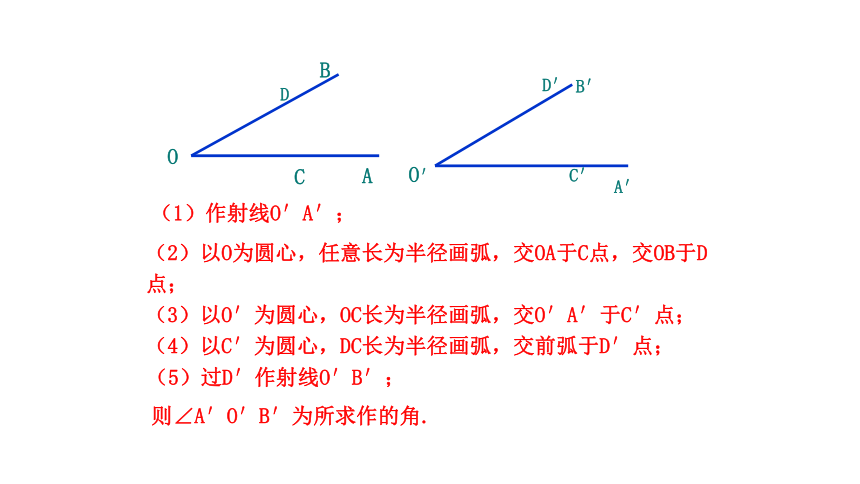
(1)作射线O′A′;
则∠A′O′B′为所求作的角.
(2)以O为圆心,任意长为半径画弧,交OA于C点,交OB于D点;
(3)以O′为圆心,OC长为半径画弧,交O′A′于C′点;
(4)以C′为圆心,DC长为半径画弧,交前弧于D′点;
已知三角形的两角及其夹边,求作三角形.
已知: ∠α,∠β ,线段a,用尺规作△ABC,使∠A =∠α, ∠ B= ∠β, AB= a.
α
G
F
a
分析:根据夹边的概念和题目所给的条件,可以考虑先作出夹边,然后再以夹边的端点作为角的顶点进一步确定两个角.
β
B
G′
F′
D
A
(1)作一条线段AB=a.
(2)以A为顶点,作∠DAB= ∠α.
(3)以B为顶点,在AB的同侧作∠EBA= ∠β,
DA与EB相交于点C.
则△ABC为所求作的三角形.
E
C
作法:
【例题1】
B
【跟踪训练】
C
【例题2】
D
【跟踪训练】
A
【例题3】
B
【跟踪训练】
C
D
2.如图是作△ABC的作图痕迹,则此作图的已知条件是 ( )
A.已知两边及夹角 B.已知三边
C.已知两角及夹边 D.已知两边及一边对角
C
10
4.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段c、直线l及l外一点A.
求作:Rt△ABC,使直角边为AC(AC⊥l,垂足为点C),斜边AB=c.
解:如图,Rt△ABC为所求作的三角形.
5.两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹.提示:角平分线上的点到角两边的距离相等)
解:如图:①作出线段AB的垂直平分线;②作出角的平分线(2条),它们的交点即为所求作的点C(2个).
知识是一种快乐,而好奇则是知识的萌芽.
——培根
2.6 用尺规作三角形
方法一:度量法,先量出已知线段的长度,再画出一条和这条线段长度相等的线段.
1.如何画一条线段等于已知线段.
2.尺规作图的一般步骤:①已知;②求作;③作法;④证明.
方法二:尺规法,用直尺画一条射线,用圆规在射线上截取线段等于已知线段.
1.经历操作实践活动,会用尺规作已知三边的三角形.
2.在作图中会用规范的作图语言,写出作图步骤.
3.掌握在给出的两边及其夹角的条件下,能够利用尺规作三角形;
4.经历操作实践活动,会用尺规作已知两角及其夹边的三角形.
已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
A
B
(5)过D′作射线O′B′;
O
A
B
C
D
O′
A′
B′
D′
C′
(1)作射线O′A′;
则∠A′O′B′为所求作的角.
(2)以O为圆心,任意长为半径画弧,交OA于C点,交OB于D点;
(3)以O′为圆心,OC长为半径画弧,交O′A′于C′点;
(4)以C′为圆心,DC长为半径画弧,交前弧于D′点;
已知三角形的两角及其夹边,求作三角形.
已知: ∠α,∠β ,线段a,用尺规作△ABC,使∠A =∠α, ∠ B= ∠β, AB= a.
α
G
F
a
分析:根据夹边的概念和题目所给的条件,可以考虑先作出夹边,然后再以夹边的端点作为角的顶点进一步确定两个角.
β
B
G′
F′
D
A
(1)作一条线段AB=a.
(2)以A为顶点,作∠DAB= ∠α.
(3)以B为顶点,在AB的同侧作∠EBA= ∠β,
DA与EB相交于点C.
则△ABC为所求作的三角形.
E
C
作法:
【例题1】
B
【跟踪训练】
C
【例题2】
D
【跟踪训练】
A
【例题3】
B
【跟踪训练】
C
D
2.如图是作△ABC的作图痕迹,则此作图的已知条件是 ( )
A.已知两边及夹角 B.已知三边
C.已知两角及夹边 D.已知两边及一边对角
C
10
4.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段c、直线l及l外一点A.
求作:Rt△ABC,使直角边为AC(AC⊥l,垂足为点C),斜边AB=c.
解:如图,Rt△ABC为所求作的三角形.
5.两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹.提示:角平分线上的点到角两边的距离相等)
解:如图:①作出线段AB的垂直平分线;②作出角的平分线(2条),它们的交点即为所求作的点C(2个).
知识是一种快乐,而好奇则是知识的萌芽.
——培根
同课章节目录
