3.1 平方根 第2课时 课件(共21张PPT) 湘教版数学八年级上册
文档属性
| 名称 | 3.1 平方根 第2课时 课件(共21张PPT) 湘教版数学八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 806.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第2课时
3.1 平方根
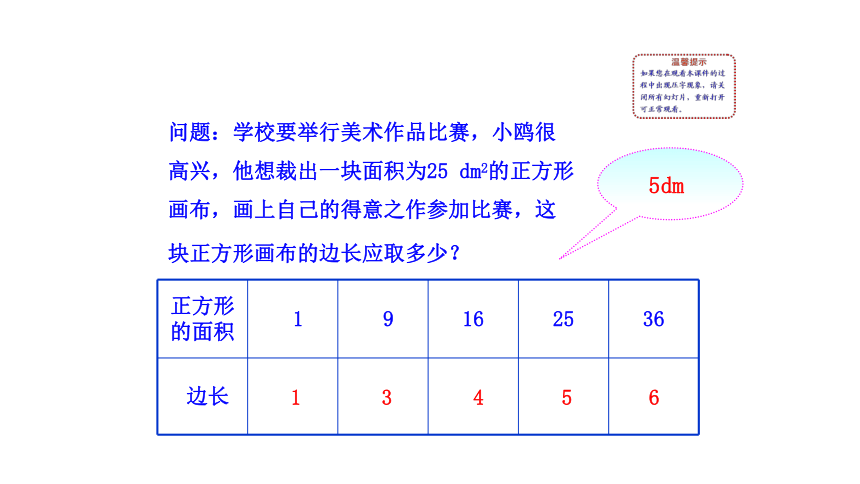
正方形的面积 1 9 16 25 36
边长
1
3
4
5
6
问题:学校要举行美术作品比赛,小鸥很高兴,他想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
5dm
1.正确理解算术平方根的概念.
2.知道算术平方根的表示方法.
3.会求一个数的算术平方根.
4.理解无理数的概念,会判断一个数是有理数还是无理数.
5.能对无理数和有理数正确分类.
特殊:0的算术平方根是0。
正数a的正平方根叫作a的算术平方根,记作 ,
读作“根号a”,a叫作被开方数.
负数有算术平方根吗?
负数没有算术平方根。
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
探索发现
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
, , 化成小数,是怎样的小数
无限不循环小数
探索发现
无限不循环的小数称为无理数.
0.101 001 000 1…(两个1之间依次多1个0),
-168.323 223 222 3…(两个3之间依次多1个2).
无理数的定义:
【例题1】
下列说法正确的是 ( )
A.有理数都是有限小数
B.除了π之外,不带根号的数都是有理数
C.不能写成分数形式的数是无理数
D.无限不循环小数不一定是无理数
C
C
【跟踪训练】
B
【例题2】
【跟踪训练】
B
正数a的正平方根叫作a的算术平方根,记作 ,读作
“根号a”,
a叫作被开方数.特殊:0的算术平方根是0。
平方根
算术平方根
无理数
无限不循环的小数称为无理数.
无理数分为正无理数和负无理数
无理数的近似数
根据实际需要,我们常用一个有限小数来近似地表示一个无理数.
对于一个无理数,我们可以采用四舍五入的方法,取一个无理数
小数点后几位,取到第几位,我们就称其为这个无理数精确到
小数点后第几位的近似值
用计算器求算术平方根
计算器型号不同,按键顺序可能有所不同,但一般先按键,然后输入数据,再按键,显示结果
C
B
D
P>Q
6.国际比赛的足球场长在100 m到110 m之间,宽在64 m到75 m之间,现有一个长方形的足球场,其长是宽的1.4倍,面积是6860 m2,则这个足球场是否能用作国际比赛?
7.如图所示是一个数值转换器的原理图,请根据原理图回答下列问题.
(1)当输入的x值为16时,求输出的y= ;
(2)是否存在x值输入后,始终不能输出y值?如果存在,请写出所有满足要求的x的值;
(3)输入一个两位数x,恰好经过两次取算术平方根才能输出无理数,则x=__________________.
25或36或49或64
X=0,1
奋斗,是理想与毅力合成的混凝土,它能架成通向彼岸的桥梁.
——巴金
第2课时
3.1 平方根
正方形的面积 1 9 16 25 36
边长
1
3
4
5
6
问题:学校要举行美术作品比赛,小鸥很高兴,他想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
5dm
1.正确理解算术平方根的概念.
2.知道算术平方根的表示方法.
3.会求一个数的算术平方根.
4.理解无理数的概念,会判断一个数是有理数还是无理数.
5.能对无理数和有理数正确分类.
特殊:0的算术平方根是0。
正数a的正平方根叫作a的算术平方根,记作 ,
读作“根号a”,a叫作被开方数.
负数有算术平方根吗?
负数没有算术平方根。
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
探索发现
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
, , 化成小数,是怎样的小数
无限不循环小数
探索发现
无限不循环的小数称为无理数.
0.101 001 000 1…(两个1之间依次多1个0),
-168.323 223 222 3…(两个3之间依次多1个2).
无理数的定义:
【例题1】
下列说法正确的是 ( )
A.有理数都是有限小数
B.除了π之外,不带根号的数都是有理数
C.不能写成分数形式的数是无理数
D.无限不循环小数不一定是无理数
C
C
【跟踪训练】
B
【例题2】
【跟踪训练】
B
正数a的正平方根叫作a的算术平方根,记作 ,读作
“根号a”,
a叫作被开方数.特殊:0的算术平方根是0。
平方根
算术平方根
无理数
无限不循环的小数称为无理数.
无理数分为正无理数和负无理数
无理数的近似数
根据实际需要,我们常用一个有限小数来近似地表示一个无理数.
对于一个无理数,我们可以采用四舍五入的方法,取一个无理数
小数点后几位,取到第几位,我们就称其为这个无理数精确到
小数点后第几位的近似值
用计算器求算术平方根
计算器型号不同,按键顺序可能有所不同,但一般先按键,然后输入数据,再按键,显示结果
C
B
D
P>Q
6.国际比赛的足球场长在100 m到110 m之间,宽在64 m到75 m之间,现有一个长方形的足球场,其长是宽的1.4倍,面积是6860 m2,则这个足球场是否能用作国际比赛?
7.如图所示是一个数值转换器的原理图,请根据原理图回答下列问题.
(1)当输入的x值为16时,求输出的y= ;
(2)是否存在x值输入后,始终不能输出y值?如果存在,请写出所有满足要求的x的值;
(3)输入一个两位数x,恰好经过两次取算术平方根才能输出无理数,则x=__________________.
25或36或49或64
X=0,1
奋斗,是理想与毅力合成的混凝土,它能架成通向彼岸的桥梁.
——巴金
同课章节目录
