4.2.3 平行线的性质 课件(共24张PPT) 2024-2025学年华师大版七年级数学上册
文档属性
| 名称 | 4.2.3 平行线的性质 课件(共24张PPT) 2024-2025学年华师大版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第四章 相交线和平行线
4.2.3 平行线的性质
华师版 七年级 上册
学习目标
掌握平行线的性质,会运用两条直线是平行关系判
断角相等或互补;
能够根据平行线的性质进行简单的推理.
重点
难点
复习旧知
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问:通过上题可知平行线的判定方法是什么?
思考:反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习旧知
新课探究
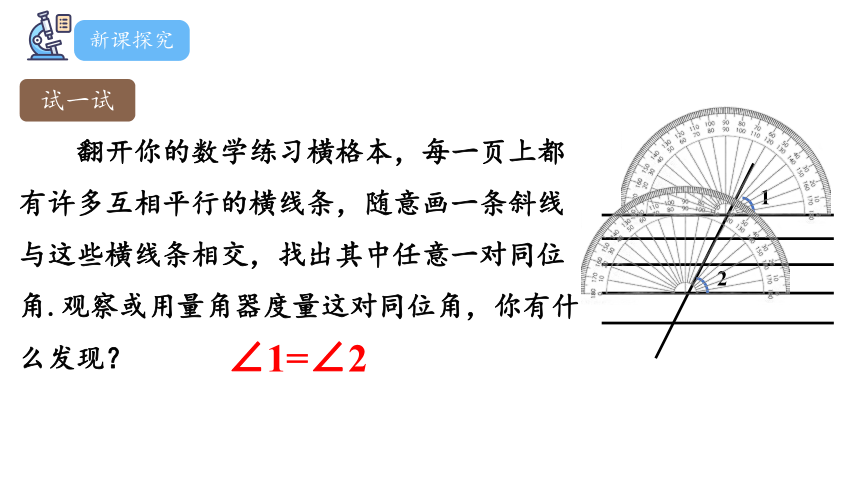
翻开你的数学练习横格本,每一页上都有许多互相平行的横线条,随意画一条斜线与这些横线条相交,找出其中任意一对同位角.观察或用量角器度量这对同位角,你有什么发现?
2
1
∠1=∠2
试一试
平行线的性质探究
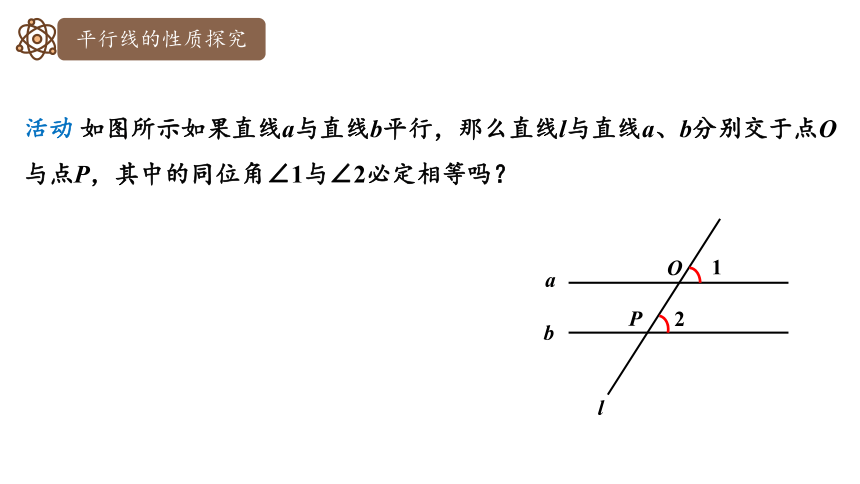
活动 如图所示如果直线a与直线b平行,那么直线l与直线a、b分别交于点O与点P,其中的同位角∠1与∠2必定相等吗?
1
2
a
b
l
O
P
平行线的性质探究
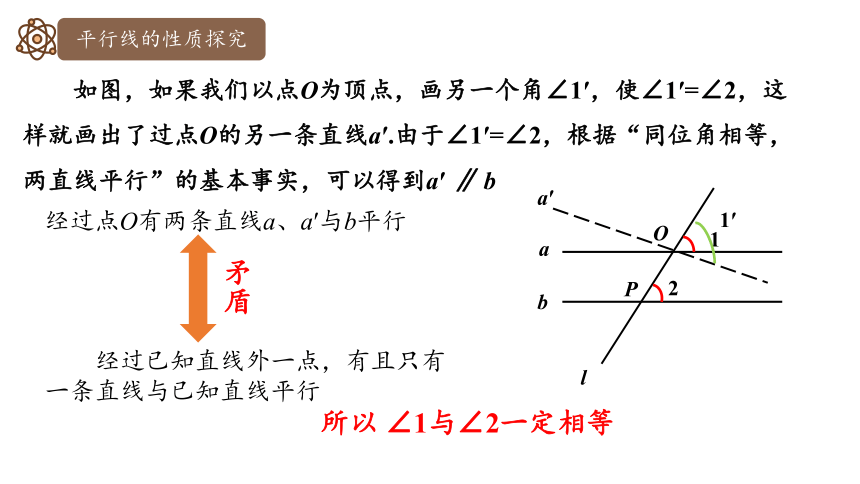
如图,如果我们以点O为顶点,画另一个角∠1′,使∠1′=∠2,这样就画出了过点O的另一条直线a′.由于∠1′=∠2,根据“同位角相等,两直线平行”的基本事实,可以得到a′ ∥ b
1
2
a
b
l
a′
1′
O
P
经过点O有两条直线a、a′与b平行
经过已知直线外一点,有且只有一条直线与已知直线平行
矛盾
所以 ∠1与∠2一定相等
平行线的性质1
两条平行直线被第三条直线所截,同位角相等.
简写成:两直线平行,同位角相等.
b
1
2
a
l
书写格式:
∵ a∥b(已知)
∴ ∠1=∠2
(两直线平行,同位角相等)
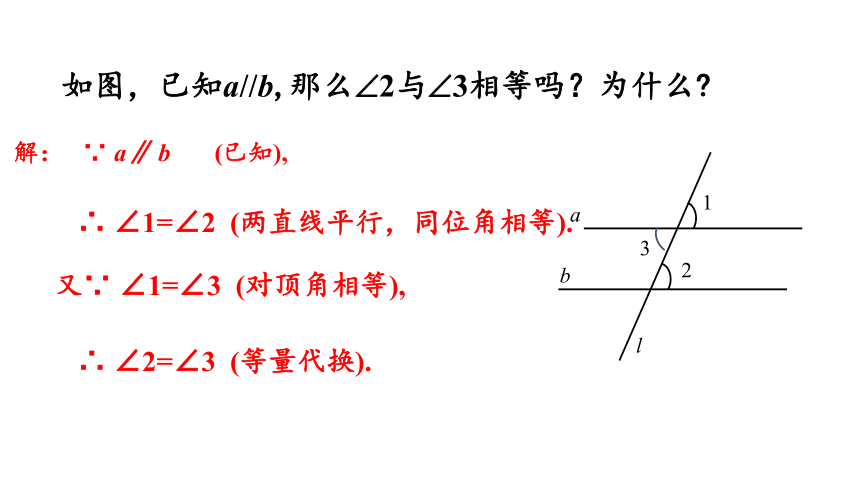
如图,已知a//b,那么 2与 3相等吗?为什么
b
1
2
a
l
3
解: ∵ a∥ b (已知),
∴ ∠1=∠2 (两直线平行,同位角相等).
又∵ ∠1=∠3 (对顶角相等),
∴ ∠2=∠3 (等量代换).
b
1
2
a
l
3
平行线的性质2
性质:两条平行直线被第三条直线所截,内错角相等.
简写成:两直线平行,内错角相等.
书写格式:
∵ a∥b(已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
l
4
思 考
∴ 2+ 4=180°(等量代换).
解: ∵a//b (已知)
∴ 1= 2(两直线平行,同位角相等)
∵ 1+ 4=180°(邻补角的性质)
平行线的性质3
性质:两条平行直线被第三条直线所截,同旁内角互补.
简写成:两直线平行,同旁内角互补.
书写格式:
∵ a∥b(已知),
∴ ∠2+∠4=180 °
(两直线平行,同旁内角互补)
b
1
2
a
l
4
总结
平行线的性质:
1.两直线平行,同位角相等;
2.两直线平行,内错角相等;
3.两直线平行,同旁内角互补。
思考
平行线的性质与判定有什么区别呢?
线的关系
角的关系
两直线平行
线的关系
同位角相等
内错角相等
同旁内角互补
角的关系
判定
平行线的性质
平行线的判定
性质
例题分析
例4 如图,已知直线 a∥ b,∠1=50°,求∠2的度数.
∴∠2=50°(等量代换)
解:∵a∥ b(已知)
∴∠1=∠2(两直线平行,内错角相等)
∵∠1=50°(已知)
例5 如图,在四边形 ABCD 中 ,AB // CD,∠B = 60°,求∠C 的度数. 能否求得 ∠A 的度数?
根据题目的已知条件,无法求出 ∠A 的度数.
解:∵ AB// CD (已知)
∴ ∠B+∠C = 180°(两直线平行,同旁内角互补).
∵ ∠B = 60° (已知),
∴ ∠C = 180°-∠B = 120°(等式的性质).
例6 将如图所示的方格图中的图形向右平行移动 4 格,再向上平行移动 3 格,画出平行移动后的图形.
解:如图2所示的图形,即为原图形,以及原图形向右平行移动4格,再向上平行移动3格后的图形.
从图中可以看出,原图形中的每一个顶点及每一条边都向右平行移动了4格,再向上平行移动了3格.
图1
图2
随堂练习
1.根据题图,在下列解答中,填上适当的理由: 【教材P192 练习 第1题】
(1)∵AD // BC (已知),
∴ ∠1 = ∠B( );
(2)∵AB // CD (已知),
∴ ∠1 = ∠D( ).
两直线平行,同位角相等
两直线平行,内错角相等
2. 在下列解答中,填空:【教材P192 练习 第2题】
(1)∵AD // BC (已知),
∴( ) + ∠ABC = 180°
(两直线平行,同旁内角互补);
(2)∵ AB // CD (已知),
∴∠ABC + ( ) = 180°
(两直线平行,同旁内角互补).
∠BAD
∠BCD
3.如图,两条平行直线a、b被第三条直线c所截.若∠1=52°,
那么∠2=_______, ∠3=_______, ∠4=_______, 【教材P192 练习 第3题】
1
2
3
4
a
b
c
52°
128°
52°
4.如图,将方格图中的图形向右平行移动3格,再向下平行移动4格,画出平行移动后的图形. 【教材P192 练习 第4题】
5.如图,已知直线a∥ b,∠3 = 131°,求∠1、∠2的度数.
阅读下面的解答过程,并填空(理由或数学式). 【教材P192 练习 第5题】
解 ∵ ∠3=131°( )
又∵∠3=∠1 ( )
∴ ∠1=( )( )
∵a ∥ b( )
∴ ∠1+ ∠2=180°( )
∴ ∠2=( )(等式的性质).
a
b
1
3
2
已知
对顶角相等
131°
等量代换
已知
两直线平行,同旁内角互补
49°
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
结论
结论
已知
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
第四章 相交线和平行线
4.2.3 平行线的性质
华师版 七年级 上册
学习目标
掌握平行线的性质,会运用两条直线是平行关系判
断角相等或互补;
能够根据平行线的性质进行简单的推理.
重点
难点
复习旧知
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问:通过上题可知平行线的判定方法是什么?
思考:反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习旧知
新课探究
翻开你的数学练习横格本,每一页上都有许多互相平行的横线条,随意画一条斜线与这些横线条相交,找出其中任意一对同位角.观察或用量角器度量这对同位角,你有什么发现?
2
1
∠1=∠2
试一试
平行线的性质探究
活动 如图所示如果直线a与直线b平行,那么直线l与直线a、b分别交于点O与点P,其中的同位角∠1与∠2必定相等吗?
1
2
a
b
l
O
P
平行线的性质探究
如图,如果我们以点O为顶点,画另一个角∠1′,使∠1′=∠2,这样就画出了过点O的另一条直线a′.由于∠1′=∠2,根据“同位角相等,两直线平行”的基本事实,可以得到a′ ∥ b
1
2
a
b
l
a′
1′
O
P
经过点O有两条直线a、a′与b平行
经过已知直线外一点,有且只有一条直线与已知直线平行
矛盾
所以 ∠1与∠2一定相等
平行线的性质1
两条平行直线被第三条直线所截,同位角相等.
简写成:两直线平行,同位角相等.
b
1
2
a
l
书写格式:
∵ a∥b(已知)
∴ ∠1=∠2
(两直线平行,同位角相等)
如图,已知a//b,那么 2与 3相等吗?为什么
b
1
2
a
l
3
解: ∵ a∥ b (已知),
∴ ∠1=∠2 (两直线平行,同位角相等).
又∵ ∠1=∠3 (对顶角相等),
∴ ∠2=∠3 (等量代换).
b
1
2
a
l
3
平行线的性质2
性质:两条平行直线被第三条直线所截,内错角相等.
简写成:两直线平行,内错角相等.
书写格式:
∵ a∥b(已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
l
4
思 考
∴ 2+ 4=180°(等量代换).
解: ∵a//b (已知)
∴ 1= 2(两直线平行,同位角相等)
∵ 1+ 4=180°(邻补角的性质)
平行线的性质3
性质:两条平行直线被第三条直线所截,同旁内角互补.
简写成:两直线平行,同旁内角互补.
书写格式:
∵ a∥b(已知),
∴ ∠2+∠4=180 °
(两直线平行,同旁内角互补)
b
1
2
a
l
4
总结
平行线的性质:
1.两直线平行,同位角相等;
2.两直线平行,内错角相等;
3.两直线平行,同旁内角互补。
思考
平行线的性质与判定有什么区别呢?
线的关系
角的关系
两直线平行
线的关系
同位角相等
内错角相等
同旁内角互补
角的关系
判定
平行线的性质
平行线的判定
性质
例题分析
例4 如图,已知直线 a∥ b,∠1=50°,求∠2的度数.
∴∠2=50°(等量代换)
解:∵a∥ b(已知)
∴∠1=∠2(两直线平行,内错角相等)
∵∠1=50°(已知)
例5 如图,在四边形 ABCD 中 ,AB // CD,∠B = 60°,求∠C 的度数. 能否求得 ∠A 的度数?
根据题目的已知条件,无法求出 ∠A 的度数.
解:∵ AB// CD (已知)
∴ ∠B+∠C = 180°(两直线平行,同旁内角互补).
∵ ∠B = 60° (已知),
∴ ∠C = 180°-∠B = 120°(等式的性质).
例6 将如图所示的方格图中的图形向右平行移动 4 格,再向上平行移动 3 格,画出平行移动后的图形.
解:如图2所示的图形,即为原图形,以及原图形向右平行移动4格,再向上平行移动3格后的图形.
从图中可以看出,原图形中的每一个顶点及每一条边都向右平行移动了4格,再向上平行移动了3格.
图1
图2
随堂练习
1.根据题图,在下列解答中,填上适当的理由: 【教材P192 练习 第1题】
(1)∵AD // BC (已知),
∴ ∠1 = ∠B( );
(2)∵AB // CD (已知),
∴ ∠1 = ∠D( ).
两直线平行,同位角相等
两直线平行,内错角相等
2. 在下列解答中,填空:【教材P192 练习 第2题】
(1)∵AD // BC (已知),
∴( ) + ∠ABC = 180°
(两直线平行,同旁内角互补);
(2)∵ AB // CD (已知),
∴∠ABC + ( ) = 180°
(两直线平行,同旁内角互补).
∠BAD
∠BCD
3.如图,两条平行直线a、b被第三条直线c所截.若∠1=52°,
那么∠2=_______, ∠3=_______, ∠4=_______, 【教材P192 练习 第3题】
1
2
3
4
a
b
c
52°
128°
52°
4.如图,将方格图中的图形向右平行移动3格,再向下平行移动4格,画出平行移动后的图形. 【教材P192 练习 第4题】
5.如图,已知直线a∥ b,∠3 = 131°,求∠1、∠2的度数.
阅读下面的解答过程,并填空(理由或数学式). 【教材P192 练习 第5题】
解 ∵ ∠3=131°( )
又∵∠3=∠1 ( )
∴ ∠1=( )( )
∵a ∥ b( )
∴ ∠1+ ∠2=180°( )
∴ ∠2=( )(等式的性质).
a
b
1
3
2
已知
对顶角相等
131°
等量代换
已知
两直线平行,同旁内角互补
49°
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
结论
结论
已知
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
