1.2.3 直线与平面的夹角——高二数学人教B版(2019)选择性必修第一册课时优化训练(含解析)
文档属性
| 名称 | 1.2.3 直线与平面的夹角——高二数学人教B版(2019)选择性必修第一册课时优化训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 698.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览




文档简介
1.2.3 直线与平面的夹角
——高二数学人教B版(2019)选择性必修第一册课时优化训练
1.在空间直角坐标系中,直线l的一个方向向量为,平面的一个法向量为,则直线l与平面所成的角为( )
A. B. C. D.
2.直线l与平面所成的角是,若直线l在内的射影与内的直线m所成的角是,则l与m所成的角是( )
A. B. C. D.
3.正三棱锥的所有棱长都相等,则侧棱与底面所成的角的正切值是( )
A. B. C. D.
4.设直线l的方向向量为a,平面的法向量为n.若,则直线l与平面所成的角为( )
A. B. C. D.
5.已知空间向量,平面的一个法向量,则直线AB与平面所成角为( )
A. B. C.或 D.或
6.在正方体中,直线与平面所成角的正弦值为( )
A. B. C. D.
7.在直三棱柱中,为等边三角形,,M是的中点,则AM与平面所成角的正弦值为( )
A. B. C. D.
8.已知四棱锥的底面为矩形,平面,,,直线PD与平面PAC所成角的正弦值为,则四棱锥的体积为( )
A.4 B. C. D.8
9.(多选)在正方体中,下列说法正确的是( )
A.
B.
C.与平面所成的角为
D.与平面ABCD所成的角为
10.(多选)已知正方体中,E,F分别为,的中点,则( )
A.直线BE与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面BFD所成角的正弦值为
11.已知向量m,n分别是直线l的方向向量和平面的法向量.若,则l与所成角的大小为__________.
12.如图,在三棱锥中,,,两两互相垂直,,,则直线与平面所成角的正弦值为________.
13.已知正方体的棱长为4,M在棱上,且,则直线与平面所成角的正弦值为__________.
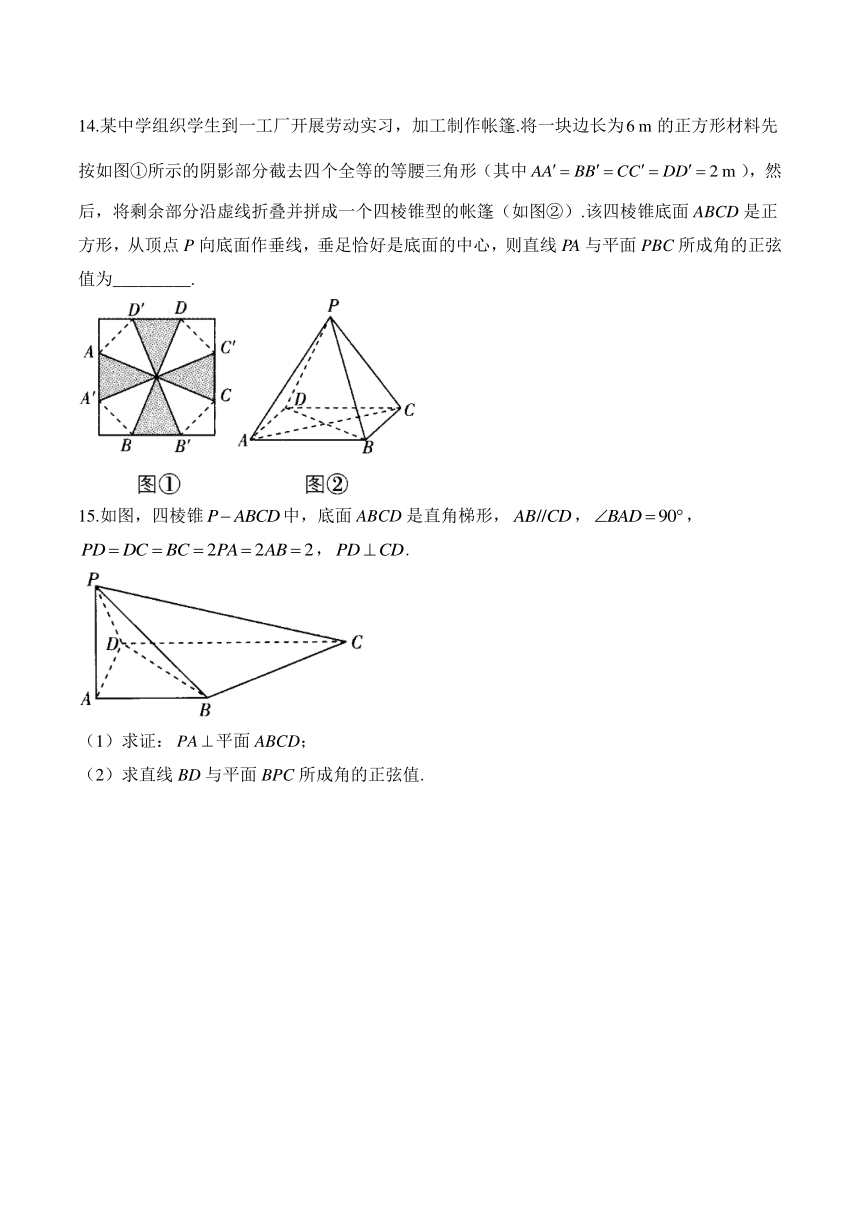
14.某中学组织学生到一工厂开展劳动实习,加工制作帐篷.将一块边长为的正方形材料先按如图①所示的阴影部分截去四个全等的等腰三角形(其中),然后,将剩余部分沿虚线折叠并拼成一个四棱锥型的帐篷(如图②).该四棱锥底面ABCD是正方形,从顶点P向底面作垂线,垂足恰好是底面的中心,则直线PA与平面PBC所成角的正弦值为_________.
15.如图,四棱锥中,底面ABCD是直角梯形,,,,.
(1)求证:平面ABCD;
(2)求直线BD与平面BPC所成角的正弦值.
答案以及解析
1.答案:A
解析:设直线l与平面所成的角为,则,所以.故选A.
2.答案:C
解析:由题意,,.由,得,.故选C.
3.答案:B
解析:设正三棱锥的底面正三角形BCD的中心为O,棱长为a,则就是侧棱AC与底面BCD所成的角,计算得.
4.答案:A
解析:由题意,设直线l与平面所成的角为,则.由,得.故选A.
5.答案:A
解析:设直线AB与平面所成角为,则,又,所以,即直线AB与平面所成角为.
6.答案:D
解析:设正方体的棱长为1,建立如图所示的空间直角坐标系,
则,,,,,,.
设平面的法向量为,
则得平面的一个法向量为.
设直线与平面所成的角为,
则.故选D.
7.答案:B
解析:如图所示,取AC的中点D,连接DM,BD,以D为原点,BD,DC,DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.
不妨设,则,,,,所以,,.设平面的法向量为,则即取,则,,所以.
设AM与平面所成角为,向量与n所成的角为,所以,即AM与平面所成角的正弦值为.故选B.
8.答案:B
解析:因为平面,平面ABCD,所以,,又,所以以D为原点,,,的方向分别为x轴、y轴、z轴正方向,建立空间直角坐标系.设,则,,,所以,.设平面PAC的法向量为,则取,得.又,与平面PAC所成角的正弦值为,所以,解得或(舍去),则,所以.
9.答案:ABD
解析:对A选项,连接,如图①,,,,,,,四边形为平行四边形,.,,故A正确.
对B选项,由题可得平面,.又,平面,平面,又平面,,故B正确.
对C选项,连接BD,交AC于点O,连接,如图②.
底面,平面ABCD,.,,平面,平面.
与平面所成的角为.设正方体的棱长为1,则,,.,,故C错误.
对D选项,底面,与平面ABCD所成的角为.易知为等腰直角三角形,,故D正确.故选ABD.
10.答案:ABC
解析:以D为坐标原点,以,,的方向分别为x,y,z轴正方向,建立空间直角坐标系.
设正方体的棱长为2,则,,,,,,,,,,则,,故,则,故直线BE与所成角为,A正确;
,,,又,故,即直线与所成角为,B正确;
,,,设平面的法向量为,则令,则,
故,因为直线与平面所成角的范围为,所以直线与平面所成角为,C正确;
,,设平面BFD的法向量为,
则令,
则,故,故直线与平面BFD所成角的正弦值为,D错误.故选ABC.
11.答案:
解析:设l与所成角为,则,.
12.答案:
解析:以O为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系(图略),
则,,,,
,,,
设平面的一个法向量为,
则
取,则,,
,
,
故直线与平面所成角的正弦值为.
13.答案:
解析:如图所示,以D为原点,,,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
则,,,,,
所以,,,设平面的一个法向量为,
则令,得,设直线与平面所成的角为,则.
14.答案:
解析:设AC与BD的交点为点O,以O为原点,OA所在直线为x轴,OB所在直线为y轴,OP所在直线为z轴建立空间直角坐标系,如图所示.
由题意可知,,,,,故,,,,.
设平面PBC的法向量为,又,,则有即
令,可得平面PBC的一个法向量为.设与平面PBC的法向量n的夹角为,则,则直线PA与平面PBC所成角的正弦值为.
15.答案:(1)证明见解析
(2)
解析:(1)证明:由于,,所以.
又,,平面PAD,
所以平面PAD,所以平面PAD,
又平面PAD,所以.
取CD的中点E,连接BE,如图.
因为底面ABCD是直角梯形,且,,
故四边形ABED为矩形,且且,
所以,又,,
所以在中,,即,
又,平面ABCD,所以平面ABCD.
(2)因为平面,,所以以点A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则,,,,,
所以,,.
设平面BPC的法向量为,
则取,可得,
所以.
所以直线BD与平面BPC所成角的正弦值为.
——高二数学人教B版(2019)选择性必修第一册课时优化训练
1.在空间直角坐标系中,直线l的一个方向向量为,平面的一个法向量为,则直线l与平面所成的角为( )
A. B. C. D.
2.直线l与平面所成的角是,若直线l在内的射影与内的直线m所成的角是,则l与m所成的角是( )
A. B. C. D.
3.正三棱锥的所有棱长都相等,则侧棱与底面所成的角的正切值是( )
A. B. C. D.
4.设直线l的方向向量为a,平面的法向量为n.若,则直线l与平面所成的角为( )
A. B. C. D.
5.已知空间向量,平面的一个法向量,则直线AB与平面所成角为( )
A. B. C.或 D.或
6.在正方体中,直线与平面所成角的正弦值为( )
A. B. C. D.
7.在直三棱柱中,为等边三角形,,M是的中点,则AM与平面所成角的正弦值为( )
A. B. C. D.
8.已知四棱锥的底面为矩形,平面,,,直线PD与平面PAC所成角的正弦值为,则四棱锥的体积为( )
A.4 B. C. D.8
9.(多选)在正方体中,下列说法正确的是( )
A.
B.
C.与平面所成的角为
D.与平面ABCD所成的角为
10.(多选)已知正方体中,E,F分别为,的中点,则( )
A.直线BE与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面BFD所成角的正弦值为
11.已知向量m,n分别是直线l的方向向量和平面的法向量.若,则l与所成角的大小为__________.
12.如图,在三棱锥中,,,两两互相垂直,,,则直线与平面所成角的正弦值为________.
13.已知正方体的棱长为4,M在棱上,且,则直线与平面所成角的正弦值为__________.
14.某中学组织学生到一工厂开展劳动实习,加工制作帐篷.将一块边长为的正方形材料先按如图①所示的阴影部分截去四个全等的等腰三角形(其中),然后,将剩余部分沿虚线折叠并拼成一个四棱锥型的帐篷(如图②).该四棱锥底面ABCD是正方形,从顶点P向底面作垂线,垂足恰好是底面的中心,则直线PA与平面PBC所成角的正弦值为_________.
15.如图,四棱锥中,底面ABCD是直角梯形,,,,.
(1)求证:平面ABCD;
(2)求直线BD与平面BPC所成角的正弦值.
答案以及解析
1.答案:A
解析:设直线l与平面所成的角为,则,所以.故选A.
2.答案:C
解析:由题意,,.由,得,.故选C.
3.答案:B
解析:设正三棱锥的底面正三角形BCD的中心为O,棱长为a,则就是侧棱AC与底面BCD所成的角,计算得.
4.答案:A
解析:由题意,设直线l与平面所成的角为,则.由,得.故选A.
5.答案:A
解析:设直线AB与平面所成角为,则,又,所以,即直线AB与平面所成角为.
6.答案:D
解析:设正方体的棱长为1,建立如图所示的空间直角坐标系,
则,,,,,,.
设平面的法向量为,
则得平面的一个法向量为.
设直线与平面所成的角为,
则.故选D.
7.答案:B
解析:如图所示,取AC的中点D,连接DM,BD,以D为原点,BD,DC,DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.
不妨设,则,,,,所以,,.设平面的法向量为,则即取,则,,所以.
设AM与平面所成角为,向量与n所成的角为,所以,即AM与平面所成角的正弦值为.故选B.
8.答案:B
解析:因为平面,平面ABCD,所以,,又,所以以D为原点,,,的方向分别为x轴、y轴、z轴正方向,建立空间直角坐标系.设,则,,,所以,.设平面PAC的法向量为,则取,得.又,与平面PAC所成角的正弦值为,所以,解得或(舍去),则,所以.
9.答案:ABD
解析:对A选项,连接,如图①,,,,,,,四边形为平行四边形,.,,故A正确.
对B选项,由题可得平面,.又,平面,平面,又平面,,故B正确.
对C选项,连接BD,交AC于点O,连接,如图②.
底面,平面ABCD,.,,平面,平面.
与平面所成的角为.设正方体的棱长为1,则,,.,,故C错误.
对D选项,底面,与平面ABCD所成的角为.易知为等腰直角三角形,,故D正确.故选ABD.
10.答案:ABC
解析:以D为坐标原点,以,,的方向分别为x,y,z轴正方向,建立空间直角坐标系.
设正方体的棱长为2,则,,,,,,,,,,则,,故,则,故直线BE与所成角为,A正确;
,,,又,故,即直线与所成角为,B正确;
,,,设平面的法向量为,则令,则,
故,因为直线与平面所成角的范围为,所以直线与平面所成角为,C正确;
,,设平面BFD的法向量为,
则令,
则,故,故直线与平面BFD所成角的正弦值为,D错误.故选ABC.
11.答案:
解析:设l与所成角为,则,.
12.答案:
解析:以O为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系(图略),
则,,,,
,,,
设平面的一个法向量为,
则
取,则,,
,
,
故直线与平面所成角的正弦值为.
13.答案:
解析:如图所示,以D为原点,,,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
则,,,,,
所以,,,设平面的一个法向量为,
则令,得,设直线与平面所成的角为,则.
14.答案:
解析:设AC与BD的交点为点O,以O为原点,OA所在直线为x轴,OB所在直线为y轴,OP所在直线为z轴建立空间直角坐标系,如图所示.
由题意可知,,,,,故,,,,.
设平面PBC的法向量为,又,,则有即
令,可得平面PBC的一个法向量为.设与平面PBC的法向量n的夹角为,则,则直线PA与平面PBC所成角的正弦值为.
15.答案:(1)证明见解析
(2)
解析:(1)证明:由于,,所以.
又,,平面PAD,
所以平面PAD,所以平面PAD,
又平面PAD,所以.
取CD的中点E,连接BE,如图.
因为底面ABCD是直角梯形,且,,
故四边形ABED为矩形,且且,
所以,又,,
所以在中,,即,
又,平面ABCD,所以平面ABCD.
(2)因为平面,,所以以点A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则,,,,,
所以,,.
设平面BPC的法向量为,
则取,可得,
所以.
所以直线BD与平面BPC所成角的正弦值为.
