3.1.1 基本计数原理——高二数学人教B版(2019)选择性必修第二册课时优化训练(含解析)
文档属性
| 名称 | 3.1.1 基本计数原理——高二数学人教B版(2019)选择性必修第二册课时优化训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览


文档简介
3.1.1 基本计数原理
——高二数学人教B版(2019)选择性必修第二册课时优化训练
1.从集合中任取两个互不相等的数a,b组成复数,其中虚数有( )
A.30个 B.42个 C.36个 D.35个
2.如图,用4种不同的颜色对A,B,C,D四个区域涂色,要求相邻的两个区域不能用同一种颜色,则不同的涂色方法有( )
A.24种 B.48种 C.72种 D.96种
3.数学与生活有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,如11,242,5225都是回文数,则用0,1,2,3,4,5这些数字构成的所有三位回文数中能被3整除的个数是
A.8 B.10 C.11 D.13
4.设集合,集合,定义,则子集的个数是( )
A. B. C. D.10
5.有四张红桃纸牌、三张黑桃纸牌及两张梅花纸牌,每张纸牌上的数字不同,取出两张不同花色的纸牌,不同的取法共有( )
A.24种 B.9种 C.10种 D.26种
6.有5个不同的棱柱、3个不同的棱锥、4个不同的圆台、2个不同的球,若从中任取多面体和旋转体各1个,则不同的取法种数是( )
A.14 B.23 C.48 D.120
7.为了备战下一届排球世锦赛,中国国家队甲、乙、丙、丁四人练习传球,第1次由甲传给乙、丙、丁三人中的任意一人,第2次由持球者传给另外三人中的任意一人,往后依此类推,经过4次传球,球仍回到甲手中,则传法总数为( )
A.30 B.24 C.21 D.12
8.在如图所示的5个区域内种植花卉,每个区域种植1种花卉,且相邻区域种植的花卉不同.若有6种不同的花卉可供选择,则不同的种植方法的种数是( )
A.1440 B.720 C.1920 D.960
9.(多选)高二年级安排甲、乙、丙三位同学到A,B,C,D,E五个社区进行暑期社会实践活动,每位同学只能选择一个社区进行活动,且多个同学可以选择同一个社区进行活动,下列说法正确的有( )
A.所有可能的方法有种
B.如果社区A必须有同学选择,则不同的安排方法有61种
C.如果同学甲必须选择社区A,则不同的安排方法有25种
D.如果甲、乙两名同学必须在同一个社区,则不同的安排方法共有20种
10.(多选)甲、乙、丙、丁、戊五只猴子在一棵枯树上玩耍,假设它们均不慎失足下落,已知:(1)甲在下落的过程中依次撞击到树枝A,B,C;(2)乙在下落的过程中依次撞击到树枝D,E,F;(3)丙在下落的过程中依次撞击到树枝G,A,C;(4)丁在下落的过程中依次撞击到树枝B,D,H;(5)戊在下落的过程中依次撞击到树枝I,C,E,则下列结论正确的是( )
A.最高处的树枝为G,I中的一个
B.最低处的树枝一定是F
C.这九根树枝从高到低不同的顺序共有33种
D.这九根树枝从高到低不同的顺序共有32种
11.某储蓄卡的密码共有6位数字,每位数字都可从0~9中任选一个,则可设置的储蓄卡密码共有___________种.
12.已知集合,集合,集合或,则当集合C中有且只有一个元素时,集合C的情况有_________种.
13.某校准备召开高中毕业生代表会,把6个代表名额分配给了高三年级的3个班,每班至少一个名额,则不同的分配方案共有__________种.
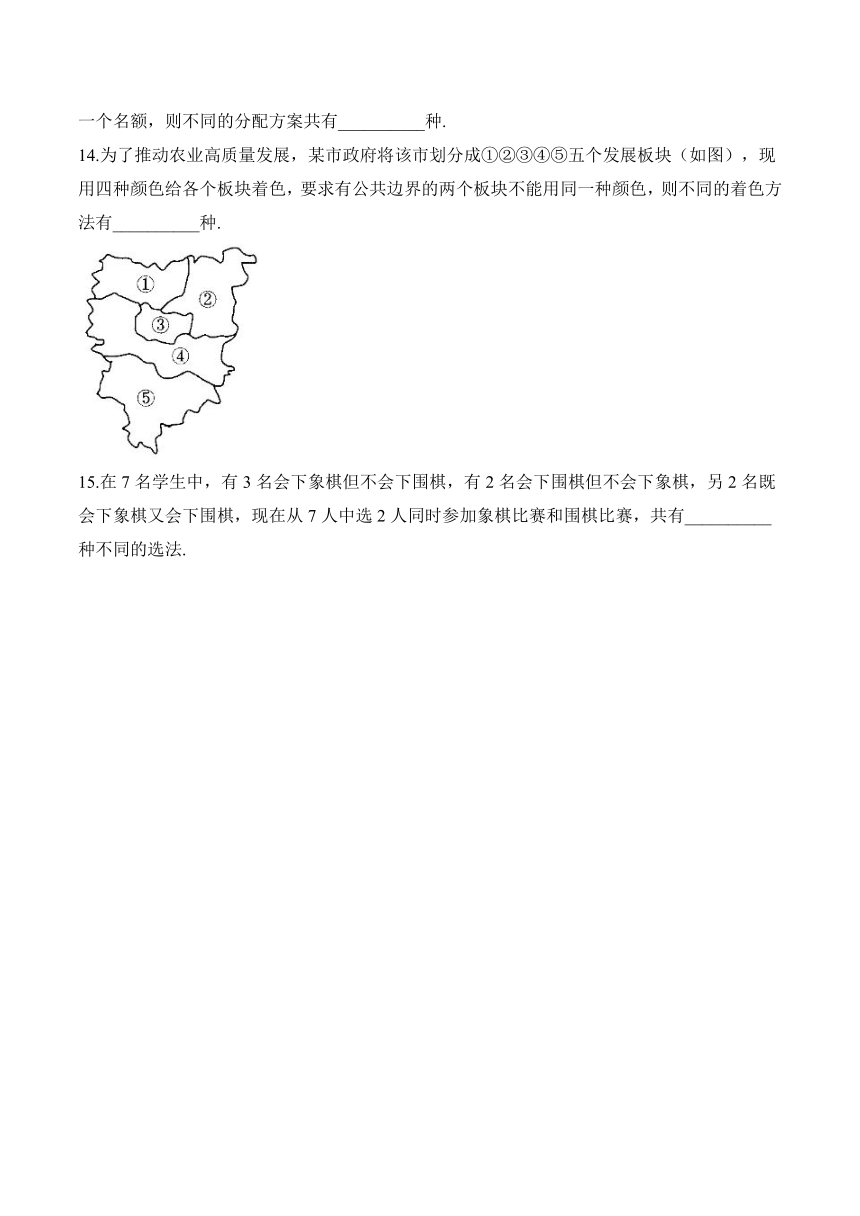
14.为了推动农业高质量发展,某市政府将该市划分成①②③④⑤五个发展板块(如图),现用四种颜色给各个板块着色,要求有公共边界的两个板块不能用同一种颜色,则不同的着色方法有__________种.
15.在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋,现在从7人中选2人同时参加象棋比赛和围棋比赛,共有__________种不同的选法.
答案以及解析
1.答案:C
解析:要完成这件事可分两步,第一步确定b,且,有6种方法;
第二步确定a,有6种方法,故由分步乘法计数原理知,共有(个)虚数,故选C.
2.答案:B
解析:按涂色顺序分四步:
涂A部分时,有4种涂法;涂B部分时,有3种涂法;
涂C部分时,有2种涂法;涂D部分时,有2种涂法.
由分步乘法计数原理,得不同的涂色方法共有(种).故选B.
3.答案:B
解析:根据题意,知三位回文数的特点是百位和个位数字相同但不能为0.当三位回文数的3个数位上的数字都相同且能被3整除时,有111,222,333,444,555,共5个;当三位回文数的百位和个位上的数字相同且能被3整除时,有141,252,303,414,525,共5个,综上,满足题意的回文数共有个,故选B.
4.答案:B
解析:因为,,所以,,又,所以x有2种情况,y有5种情况,则由分步乘法计数原理可得的元素个数为,所以子集的个数是.故选B.
5.答案:D
解析:因为取出的纸牌为两张不同花色,所以可以分成三类:红桃+黑桃:(种);红桃+梅花:(种);黑桃+梅花:(种).
故取出两张不同花色的纸牌,共有(种)不同的取法,故选D.
6.答案:C
解析:分两步:第一步,取多面体,可以从5个不同的棱柱或3个不同的棱锥中取一个,根据分类加法计数原理有(种)不同的取法;
第二步,取旋转体,可以从4个不同的圆台或2个不同的球中取一个,根据分类加法计数原理有(种)不同的取法.
所以根据分步乘法计数原理知,不同的取法种数是.故选C.
7.答案:C
解析:由题意,四人练习传球,第1次由甲传给乙、丙、丁三人中的任意一人,第2次由持球者传给另外三人中的任意一人,经过4次传球,球仍回到甲手中,
第1次传球有3种方法,第2次传球后分成“在甲手中”和“不在甲手中”两类,
第3次传球后,球一定不在甲手中,第4次传球只能在甲手中.
当第2次传球后球在甲手中时,第3次传球可能为丙或乙或丁,共3种方法;
第2次传球后球不在甲手中时,有2种方法,则第3次传球有2种方法.
经过4次传球,球仍回到甲手中的传法总数为.故选C.
8.答案:C
解析:如图,设5个区域分别是A,B,C,D,E.
第一步:选择1种花卉种植在B区域,有6种选法.
第二步:从剩下的5种不同的花卉中选择1种种植在A区域,有5种选法.
第三步:从剩下的4种花卉中选择1种种植在C区域,有4种选法.
第四步:区域D与区域B和区域C种植的花卉不同,则区域D可选择的花卉有4种.
第五步:区域E与区域D和区域B种植的花卉不同,则区域E可选择的花卉有4种.
故不同的种植方法的种数是.故选C.
9.答案:BC
解析:对于选项A,安排甲、乙、丙三位同学到A,B,C,D,E五个社区进行暑期社会实践活动,每位同学只能选择一个社区进行活动,且多个同学可以选择同一个社区进行活动,
故有种选择方案,错误;
对于选项B,如果社区A必须有同学选择,则不同的安排方法有(种),正确;
对于选项C:如果同学甲必须选择社区A,则不同的安排方法有(种),正确;
对于选项D:如果甲、乙两名同学必须在同一个社区,再分为丙与甲、乙两名同学在一起和不在一起两种情况,则不同的安排方法共有(种),错误.故选BC.
10.答案:AC
解析:由题判断出部分树枝由高到低的顺序为,还剩下D,H,I,且树枝I比C高,树枝D在树枝B,E之间,树枝H比D低,最高可能为G或I,最低为F或H,故A选项正确,B错误;
先看树枝I,有4种可能,若I在B,C之间,
则C有3种可能:①D在B,I之间,H有5种可能;
②D在I,C之间,H有4种可能;
③D在C,E之间,H有3种可能,
此时树枝的高低顺序有(种)。
若I不在B,C之间,则I有3种可能,D有2中可能,
若D在B,C之间,则H有3种可能,
若D在C,E之间,则H有三种可能,
此时树枝的高低顺序有(种)可能,
故这九根树枝从高到低不同的顺序共有种,故C选项正确.故选:AC.
11.答案:
解析:每位上都有10个数字可选,由分步乘法计数原理知共有种.
12.答案:7
解析:分两种情况:当集合C中的元素属于集合A时,有3种情况;当集合C中的元素属于集合B时,有4种情况.集合A与集合B无公共元素,集合C的情况共有(种).
13.答案:10
解析:根据题意,3个班选出的6个代表名额分三种情况:
第一种情况,代表名额为2,2,2,有1种;
第二种情况,代表名额为3,2,1,有种;
第三种情况,代表名额为4,1,1,有3种.
所以不同的分配方案共有种.
14.答案:72
解析:先涂区域③,有4种颜色选择,接下来涂区域④,有3种颜色选择,再涂区域①②,涂区域①有2种颜色选择,涂区域②有1种颜色选择,最后涂区域⑤,有3种颜色选择,故由分步乘法计数原理可知,不同的着色方法种数为种.
15.答案:18
解析:选参加象棋比赛的学生有两种方法:在只会下象棋的3人中选或在既会下象棋又会下围棋的2人中选;选参加围棋比赛的学生也有两种选法:在只会下围棋的2人中选或在既会下象棋又会下围棋的2人中选.互相搭配,可得四类不同的选法.
第一类:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只会下围棋的学生中选1名参加围棋比赛,有(种)选法;
第二类:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加围棋比赛,有(种)选法;
第三类:从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加象棋比赛,有(种)选法;
第四类:2名既会下象棋又会下围棋的学生分别参加象棋比赛和围棋比赛,有2种选法.
所以共有(种)不同的选法.
——高二数学人教B版(2019)选择性必修第二册课时优化训练
1.从集合中任取两个互不相等的数a,b组成复数,其中虚数有( )
A.30个 B.42个 C.36个 D.35个
2.如图,用4种不同的颜色对A,B,C,D四个区域涂色,要求相邻的两个区域不能用同一种颜色,则不同的涂色方法有( )
A.24种 B.48种 C.72种 D.96种
3.数学与生活有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,如11,242,5225都是回文数,则用0,1,2,3,4,5这些数字构成的所有三位回文数中能被3整除的个数是
A.8 B.10 C.11 D.13
4.设集合,集合,定义,则子集的个数是( )
A. B. C. D.10
5.有四张红桃纸牌、三张黑桃纸牌及两张梅花纸牌,每张纸牌上的数字不同,取出两张不同花色的纸牌,不同的取法共有( )
A.24种 B.9种 C.10种 D.26种
6.有5个不同的棱柱、3个不同的棱锥、4个不同的圆台、2个不同的球,若从中任取多面体和旋转体各1个,则不同的取法种数是( )
A.14 B.23 C.48 D.120
7.为了备战下一届排球世锦赛,中国国家队甲、乙、丙、丁四人练习传球,第1次由甲传给乙、丙、丁三人中的任意一人,第2次由持球者传给另外三人中的任意一人,往后依此类推,经过4次传球,球仍回到甲手中,则传法总数为( )
A.30 B.24 C.21 D.12
8.在如图所示的5个区域内种植花卉,每个区域种植1种花卉,且相邻区域种植的花卉不同.若有6种不同的花卉可供选择,则不同的种植方法的种数是( )
A.1440 B.720 C.1920 D.960
9.(多选)高二年级安排甲、乙、丙三位同学到A,B,C,D,E五个社区进行暑期社会实践活动,每位同学只能选择一个社区进行活动,且多个同学可以选择同一个社区进行活动,下列说法正确的有( )
A.所有可能的方法有种
B.如果社区A必须有同学选择,则不同的安排方法有61种
C.如果同学甲必须选择社区A,则不同的安排方法有25种
D.如果甲、乙两名同学必须在同一个社区,则不同的安排方法共有20种
10.(多选)甲、乙、丙、丁、戊五只猴子在一棵枯树上玩耍,假设它们均不慎失足下落,已知:(1)甲在下落的过程中依次撞击到树枝A,B,C;(2)乙在下落的过程中依次撞击到树枝D,E,F;(3)丙在下落的过程中依次撞击到树枝G,A,C;(4)丁在下落的过程中依次撞击到树枝B,D,H;(5)戊在下落的过程中依次撞击到树枝I,C,E,则下列结论正确的是( )
A.最高处的树枝为G,I中的一个
B.最低处的树枝一定是F
C.这九根树枝从高到低不同的顺序共有33种
D.这九根树枝从高到低不同的顺序共有32种
11.某储蓄卡的密码共有6位数字,每位数字都可从0~9中任选一个,则可设置的储蓄卡密码共有___________种.
12.已知集合,集合,集合或,则当集合C中有且只有一个元素时,集合C的情况有_________种.
13.某校准备召开高中毕业生代表会,把6个代表名额分配给了高三年级的3个班,每班至少一个名额,则不同的分配方案共有__________种.
14.为了推动农业高质量发展,某市政府将该市划分成①②③④⑤五个发展板块(如图),现用四种颜色给各个板块着色,要求有公共边界的两个板块不能用同一种颜色,则不同的着色方法有__________种.
15.在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋,现在从7人中选2人同时参加象棋比赛和围棋比赛,共有__________种不同的选法.
答案以及解析
1.答案:C
解析:要完成这件事可分两步,第一步确定b,且,有6种方法;
第二步确定a,有6种方法,故由分步乘法计数原理知,共有(个)虚数,故选C.
2.答案:B
解析:按涂色顺序分四步:
涂A部分时,有4种涂法;涂B部分时,有3种涂法;
涂C部分时,有2种涂法;涂D部分时,有2种涂法.
由分步乘法计数原理,得不同的涂色方法共有(种).故选B.
3.答案:B
解析:根据题意,知三位回文数的特点是百位和个位数字相同但不能为0.当三位回文数的3个数位上的数字都相同且能被3整除时,有111,222,333,444,555,共5个;当三位回文数的百位和个位上的数字相同且能被3整除时,有141,252,303,414,525,共5个,综上,满足题意的回文数共有个,故选B.
4.答案:B
解析:因为,,所以,,又,所以x有2种情况,y有5种情况,则由分步乘法计数原理可得的元素个数为,所以子集的个数是.故选B.
5.答案:D
解析:因为取出的纸牌为两张不同花色,所以可以分成三类:红桃+黑桃:(种);红桃+梅花:(种);黑桃+梅花:(种).
故取出两张不同花色的纸牌,共有(种)不同的取法,故选D.
6.答案:C
解析:分两步:第一步,取多面体,可以从5个不同的棱柱或3个不同的棱锥中取一个,根据分类加法计数原理有(种)不同的取法;
第二步,取旋转体,可以从4个不同的圆台或2个不同的球中取一个,根据分类加法计数原理有(种)不同的取法.
所以根据分步乘法计数原理知,不同的取法种数是.故选C.
7.答案:C
解析:由题意,四人练习传球,第1次由甲传给乙、丙、丁三人中的任意一人,第2次由持球者传给另外三人中的任意一人,经过4次传球,球仍回到甲手中,
第1次传球有3种方法,第2次传球后分成“在甲手中”和“不在甲手中”两类,
第3次传球后,球一定不在甲手中,第4次传球只能在甲手中.
当第2次传球后球在甲手中时,第3次传球可能为丙或乙或丁,共3种方法;
第2次传球后球不在甲手中时,有2种方法,则第3次传球有2种方法.
经过4次传球,球仍回到甲手中的传法总数为.故选C.
8.答案:C
解析:如图,设5个区域分别是A,B,C,D,E.
第一步:选择1种花卉种植在B区域,有6种选法.
第二步:从剩下的5种不同的花卉中选择1种种植在A区域,有5种选法.
第三步:从剩下的4种花卉中选择1种种植在C区域,有4种选法.
第四步:区域D与区域B和区域C种植的花卉不同,则区域D可选择的花卉有4种.
第五步:区域E与区域D和区域B种植的花卉不同,则区域E可选择的花卉有4种.
故不同的种植方法的种数是.故选C.
9.答案:BC
解析:对于选项A,安排甲、乙、丙三位同学到A,B,C,D,E五个社区进行暑期社会实践活动,每位同学只能选择一个社区进行活动,且多个同学可以选择同一个社区进行活动,
故有种选择方案,错误;
对于选项B,如果社区A必须有同学选择,则不同的安排方法有(种),正确;
对于选项C:如果同学甲必须选择社区A,则不同的安排方法有(种),正确;
对于选项D:如果甲、乙两名同学必须在同一个社区,再分为丙与甲、乙两名同学在一起和不在一起两种情况,则不同的安排方法共有(种),错误.故选BC.
10.答案:AC
解析:由题判断出部分树枝由高到低的顺序为,还剩下D,H,I,且树枝I比C高,树枝D在树枝B,E之间,树枝H比D低,最高可能为G或I,最低为F或H,故A选项正确,B错误;
先看树枝I,有4种可能,若I在B,C之间,
则C有3种可能:①D在B,I之间,H有5种可能;
②D在I,C之间,H有4种可能;
③D在C,E之间,H有3种可能,
此时树枝的高低顺序有(种)。
若I不在B,C之间,则I有3种可能,D有2中可能,
若D在B,C之间,则H有3种可能,
若D在C,E之间,则H有三种可能,
此时树枝的高低顺序有(种)可能,
故这九根树枝从高到低不同的顺序共有种,故C选项正确.故选:AC.
11.答案:
解析:每位上都有10个数字可选,由分步乘法计数原理知共有种.
12.答案:7
解析:分两种情况:当集合C中的元素属于集合A时,有3种情况;当集合C中的元素属于集合B时,有4种情况.集合A与集合B无公共元素,集合C的情况共有(种).
13.答案:10
解析:根据题意,3个班选出的6个代表名额分三种情况:
第一种情况,代表名额为2,2,2,有1种;
第二种情况,代表名额为3,2,1,有种;
第三种情况,代表名额为4,1,1,有3种.
所以不同的分配方案共有种.
14.答案:72
解析:先涂区域③,有4种颜色选择,接下来涂区域④,有3种颜色选择,再涂区域①②,涂区域①有2种颜色选择,涂区域②有1种颜色选择,最后涂区域⑤,有3种颜色选择,故由分步乘法计数原理可知,不同的着色方法种数为种.
15.答案:18
解析:选参加象棋比赛的学生有两种方法:在只会下象棋的3人中选或在既会下象棋又会下围棋的2人中选;选参加围棋比赛的学生也有两种选法:在只会下围棋的2人中选或在既会下象棋又会下围棋的2人中选.互相搭配,可得四类不同的选法.
第一类:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只会下围棋的学生中选1名参加围棋比赛,有(种)选法;
第二类:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加围棋比赛,有(种)选法;
第三类:从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加象棋比赛,有(种)选法;
第四类:2名既会下象棋又会下围棋的学生分别参加象棋比赛和围棋比赛,有2种选法.
所以共有(种)不同的选法.
