4.3.2 独立性检验——高二数学人教B版(2019)选择性必修第二册课时优化训练(含解析)
文档属性
| 名称 | 4.3.2 独立性检验——高二数学人教B版(2019)选择性必修第二册课时优化训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览




文档简介
4.3.2 独立性检验
——高二数学人教B版(2019)选择性必修第二册课时优化训练
1.若由列联表中的数据计算得,则有_________的把握认为两个变量有关系( )
0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
A. B. C. D.
2.某医疗机构通过抽样调查(样本容量),利用列联表和统计量研究患肺病是否与吸烟有关.计算得,经查对临界值表知,现给出四个结论,其中正确的是( )
A.在100个吸烟的人中约有95个人患肺病
B.若某人吸烟,那么他有95%的可能性患肺病
C.有95%的把握认为“患肺病与吸烟有关”
D.只有5%的把握认为“患肺病与吸烟有关”
3.根据分类变量x与y的成对样本数据,计算得到.依据的独立性检验,结论为( )
A.变量x与变量y不独立.
B.变量x与变量y不独立,这个结论犯错误的概率不超过0.01
C.变量x与变量y独立
D.变量x与变量y独立,这个结论犯错误的概率不超过0.01
4.某课外兴趣小组通过随机调查,利用列联表和统计量研究数学成绩优秀是否与性别有关.计算得,经查表知,则下列判断正确的是( )
A.每100个数学成绩优秀的人中就会有1名是女生
B.若某人数学成绩优秀,那么他为男生的概率是0.010
C.有的把握认为“数学成绩优秀与性别无关”
D.在犯错误的概率不超过的前提下认为“数学成绩优秀与性别有关”
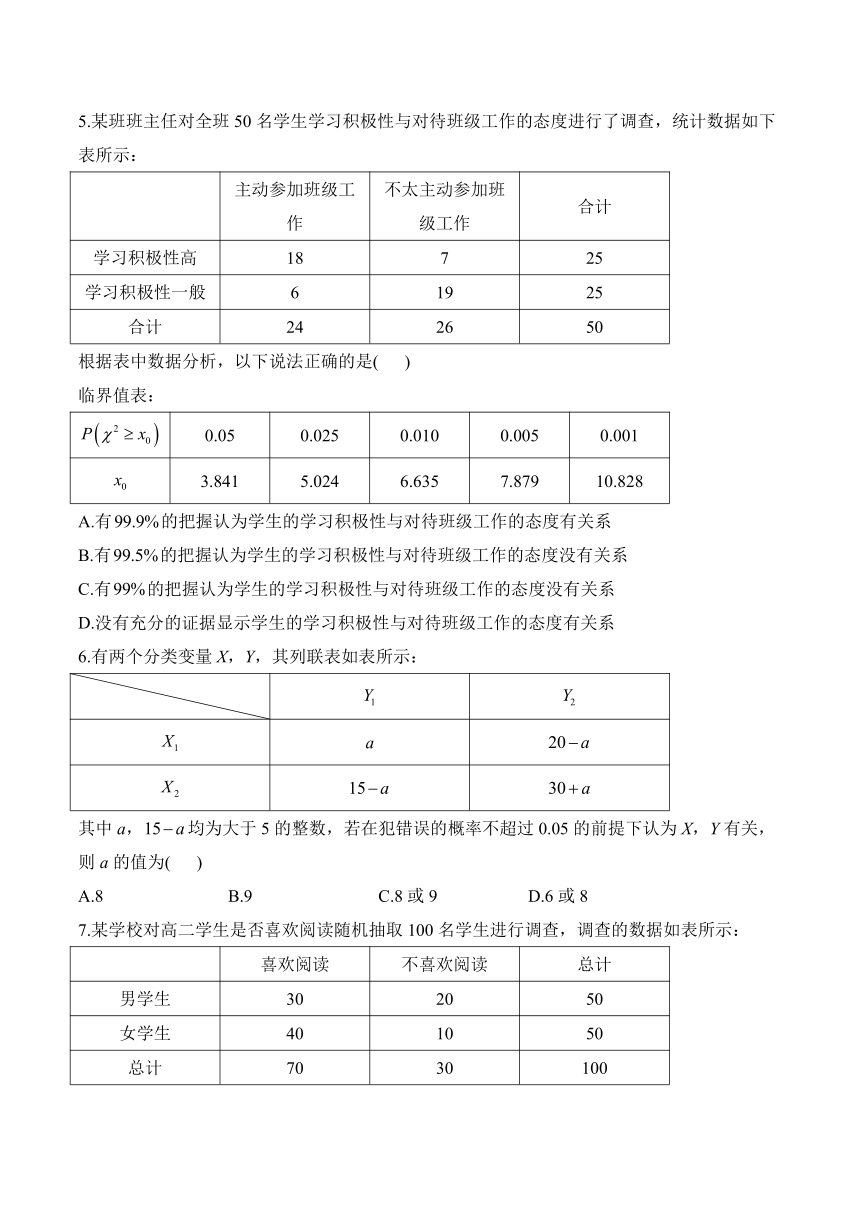
5.某班班主任对全班50名学生学习积极性与对待班级工作的态度进行了调查,统计数据如下表所示:
主动参加班级工作 不太主动参加班级工作 合计
学习积极性高 18 7 25
学习积极性一般 6 19 25
合计 24 26 50
根据表中数据分析,以下说法正确的是( )
临界值表:
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
A.有的把握认为学生的学习积极性与对待班级工作的态度有关系
B.有的把握认为学生的学习积极性与对待班级工作的态度没有关系
C.有的把握认为学生的学习积极性与对待班级工作的态度没有关系
D.没有充分的证据显示学生的学习积极性与对待班级工作的态度有关系
6.有两个分类变量X,Y,其列联表如表所示:
a
其中a,均为大于5的整数,若在犯错误的概率不超过0.05的前提下认为X,Y有关,则a的值为( )
A.8 B.9 C.8或9 D.6或8
7.某学校对高二学生是否喜欢阅读随机抽取100名学生进行调查,调查的数据如表所示:
喜欢阅读 不喜欢阅读 总计
男学生 30 20 50
女学生 40 10 50
总计 70 30 100
根据表中的数据,下列对该校高二学生的说法正确的是( )
附:.
0.10 0.05 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
A.没有以上的把握认为“性别与是否喜欢阅读有关”
B.有以上的把握认为“性别与是否喜欢阅读有关”
C.在犯错误的概率不超过0.025的前提下认为“性别与是否喜欢阅读有关”
D.在犯错误的概率不超过0.05的前提下认为“性别与是否喜欢阅读有关”
8.两个分类变量X和Y,其列联表如表,对同一样本,以下数据能说明X与Y有关联的可能性最大的一组为( )
X Y 总计
3 6 9
m 8
总计 14
A. B. C. D.
9.(多选)某中学为了解性别因素是否对本校学生体育锻炼的经常性有影响,从本校所有学生中随机调查了50名男生和50名女生,得到如下表格:
经常体育锻炼 不经常体育锻炼
男 40 10
女 30 20
附:,.
0.1 0.05 0.01
k 2.706 3.841 6.635
经计算,则可以推断出( )
A.该学校男生中经常体育锻炼的概率的估计值为
B.该学校女生中经常体育锻炼的概率的估计值为
C.有的把握认为男、女生在体育锻炼的经常性方面有差异
D.有的把握认为男、女生在体育锻炼的经常性方面有差异
10.(多选)为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法共抽取88名学生,通过测验判断其数学成绩是否优秀,得到了如下列联表:
学校 数学成绩 总计
不优秀 优秀
甲校 33 10 43
乙校 38 7 45
总计 71 17 88
已知,根据表中数据,计算得到.
0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
则下列说法正确的是( )
A.在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率没有差异
B.在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率有差异
C.若将表中所有数据都扩大为原来的10倍,在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率有差异
D.若将表中所有数据都扩大为原来的10倍,在犯错误的概率不超过0.001的前提下,可以认为两校的数学成绩优秀率没有差异
11.博鳌亚洲论坛2022年年会于4月20日至4月22日在海南博鳌镇举行.为了搞好对外宣传工作,会务组选聘了50名记者负责对外翻译工作,在下面“性别与会俄语”的列联表中,___________.
会俄语 不会俄语 总计
男 a b 20
女 6 d
总计 18 50
12.为了判断高二年级学生是否选修文科与性别的关系,现随机抽取50名高二年级学生,得到如下列联表.
理科 文科
男 13 10
女 7 20
已知,.根据表中数据,得到,则认为学生选修文科与性别有关系出错的可能性为___________.
13.有两个分类变量x和y,其中一组观测值为如表所示的列联表:
总计
a 15
50
总计 20 45 65
其中a,均为大于5的整数,则_________时,在犯错误的概率不超过0.01的前提下可以认为“x和y之间有关系”.
附:.
0.10 0.05 0.010 0.005
k 2.706 3.841 6.635 7.879
14.新疆某农科所为了研究不同土壤环境下棉花的品质,选取了甲、乙两块试验田进行种植.在棉花成熟后采摘,分别从甲、乙两块试验田采摘的棉花中各随机抽取50份样本,测定其马克隆值,整理测量数据得到如下列联表(单位:份),其中且.
注:棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标,是棉花纤维重要的内在质量指标之一.根据国家标准规定,马克隆值可分为A,B,C三个级别,A级品质最好,B级品质为标准,C级品质最差.
A级或B级 C级 合计
甲试验田 a 50
乙试验田 50
合计 80 20 100
当时,有的把握认为该品种棉花的马克隆值级别与土壤环境有关,则的最小值为____________.
附:,其中.
0.05 0.010 0.001
3.841 6.635 10.828
15.为响应国家使用新能源的号召,促进“碳达峰、碳中和”的目标实现,某汽车生产企业在积极上市四款新能源汽车后,对它们进行了市场调研.该企业研发部门从购买这四款车的车主中随机抽取了50人,让车主对所购汽车的性能进行评分,每款车的性能都有1分、2分、3分、4分、5分五个等级,各款车的评分及相应人数的统计结果如下表.
汽车款式 性能评分
1 2 3 4 5
基础版 基础版1 2 2 3 1 0
基础版2 4 4 5 3 1
豪华版 豪华版1 1 3 5 4 1
豪华版2 0 0 3 5 3
(1)求所抽车主对这四款车性能评分的平均数和分位数.
(2)当评分不小于4时,认为该款车性能优秀,否则认为性能一般.根据上述样本数据,完成以下列联表,那么在犯错误的概率不超过0.05的前提下,能否认为汽车的性能与款式有关?并解释所得结论的实际含义.
汽车性能 汽车款式 总计
基础版 豪华版
一般
优秀
总计
附:,.
0.10 0.05 0.01 0.005
k 2.706 3.841 6.635 7.879
答案以及解析
1.答案:C
解析:因为,所以有的把握认为两个变量有关系.故选C.
2.答案:C
解析:计算得,经查对临界值表知,
有的把握说患肺病与吸烟有关,故选C.
3.答案:C
解析:按照独立性检验的知识及比对的参数值,当,我们可以下结论变量x与变量y独立.故排除选项A,B;依据的独立性检验,,所以我们不能得到“变量x与变量y独立,这个结论犯错误的概率不超过0.01”这个结论.故C正确,D错误.故选C.
4.答案:D
解析:,有的把握认为“数学成绩优秀与性别有关”,即在犯错误的概率不超过的前提下认为“数学成绩优秀与性别有关”.所以ABC错误,故选D.
5.答案:A
解析:因为,所以有的把握认为学生的学习积极性与对待班级工作的态度有关系,故选A.
6.答案:C
解析:根据公式,得,
又且,,求得当或9时满足题意.故选C.
7.答案:D
解析:.
选项A,因为,所以有以上的把握认为“性别与是否喜欢阅读有关”,故A错误;
选项B,因为,所以没有以上的把握认为“性别与是否喜欢阅读有关”,故B错误;
选项C,因为,所以在犯错误的概率不超过0.025的前提下,不能认为“性别与是否喜欢阅读有关”,故C错误;
选项D,因为,所以在犯错误的概率不超过0.05的前提下认为“性别与是否喜欢阅读有关”,故D正确.故选D.
8.答案:D
解析:由给定的列联表,
对于A,,,
对于B,,,
对于C,,,
对于D,,,
显然0.2086最大,因此选项D中数据求得最大,说明X与Y有关联的可能性最大.故选D.
9.答案:BC
解析:选项A,该学校男生中经常体育锻炼的概率的估计值为,A错误;
选项B,女生中经常体育锻炼的概率的估计值为,B正确.
选项C,,故有的把握认为男、女生在体育锻炼的经常性方面有差异,C正确.
选项D,,故没有的把握认为男、女生在体育锻炼的经常性方面有差异,D错误.故选BC.
10.答案:ACD
解析:由题意可知,所以在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率没有差异,故选项A正确,选项B错误;
若将表中所有数据都扩大为原来的10倍,则,所以在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率有差异,故选项C正确;
若将表中所有数据都扩大为原来的10倍,则,所以在犯错误的概率不超过0.001的前提下,可以认为两校的数学成绩优秀率没有差异,故选项D正确,故选ACD.
11.答案:28
解析:由题得解得所以.
12.答案:
解析:,且,
认为学生选修文科与性别有关系出错的可能性为.
13.答案:9
解析:由题意知,
则,
解得或,因为且,,
所以,,所以.
14.答案:46
解析:依题意,得,
故,
整理,得,即,
因为且,
所以,所以,
又,所以的最小值为46.
15.答案:(1)平均数为3,分位数为4.5
(2)列联表中见解析;在犯错误的概率不超过0.05的前提下,认为汽车性能与款式有关;含义见解析
解析:(1)由题意得这四款车性能评分的平均数为
.
由知其分位数为.
(2)由题意得列联表如下所示:
汽车性能 汽车款式 总计
基础版 豪华版
一般 20 12 32
优秀 5 13 18
总计 25 25 50
根据列联表中的数据,经计算得到.
所以在犯错误的概率不超过0.05的前提下,认为汽车性能与款式有关.
汽车性能一般中,基础版和豪华版的频率分别为和;
汽车性能优秀中,基础版和豪华版的频率分别为和,
根据频率稳定于概率的原理,可以认为性能优秀时豪华版的概率大.
——高二数学人教B版(2019)选择性必修第二册课时优化训练
1.若由列联表中的数据计算得,则有_________的把握认为两个变量有关系( )
0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
A. B. C. D.
2.某医疗机构通过抽样调查(样本容量),利用列联表和统计量研究患肺病是否与吸烟有关.计算得,经查对临界值表知,现给出四个结论,其中正确的是( )
A.在100个吸烟的人中约有95个人患肺病
B.若某人吸烟,那么他有95%的可能性患肺病
C.有95%的把握认为“患肺病与吸烟有关”
D.只有5%的把握认为“患肺病与吸烟有关”
3.根据分类变量x与y的成对样本数据,计算得到.依据的独立性检验,结论为( )
A.变量x与变量y不独立.
B.变量x与变量y不独立,这个结论犯错误的概率不超过0.01
C.变量x与变量y独立
D.变量x与变量y独立,这个结论犯错误的概率不超过0.01
4.某课外兴趣小组通过随机调查,利用列联表和统计量研究数学成绩优秀是否与性别有关.计算得,经查表知,则下列判断正确的是( )
A.每100个数学成绩优秀的人中就会有1名是女生
B.若某人数学成绩优秀,那么他为男生的概率是0.010
C.有的把握认为“数学成绩优秀与性别无关”
D.在犯错误的概率不超过的前提下认为“数学成绩优秀与性别有关”
5.某班班主任对全班50名学生学习积极性与对待班级工作的态度进行了调查,统计数据如下表所示:
主动参加班级工作 不太主动参加班级工作 合计
学习积极性高 18 7 25
学习积极性一般 6 19 25
合计 24 26 50
根据表中数据分析,以下说法正确的是( )
临界值表:
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
A.有的把握认为学生的学习积极性与对待班级工作的态度有关系
B.有的把握认为学生的学习积极性与对待班级工作的态度没有关系
C.有的把握认为学生的学习积极性与对待班级工作的态度没有关系
D.没有充分的证据显示学生的学习积极性与对待班级工作的态度有关系
6.有两个分类变量X,Y,其列联表如表所示:
a
其中a,均为大于5的整数,若在犯错误的概率不超过0.05的前提下认为X,Y有关,则a的值为( )
A.8 B.9 C.8或9 D.6或8
7.某学校对高二学生是否喜欢阅读随机抽取100名学生进行调查,调查的数据如表所示:
喜欢阅读 不喜欢阅读 总计
男学生 30 20 50
女学生 40 10 50
总计 70 30 100
根据表中的数据,下列对该校高二学生的说法正确的是( )
附:.
0.10 0.05 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
A.没有以上的把握认为“性别与是否喜欢阅读有关”
B.有以上的把握认为“性别与是否喜欢阅读有关”
C.在犯错误的概率不超过0.025的前提下认为“性别与是否喜欢阅读有关”
D.在犯错误的概率不超过0.05的前提下认为“性别与是否喜欢阅读有关”
8.两个分类变量X和Y,其列联表如表,对同一样本,以下数据能说明X与Y有关联的可能性最大的一组为( )
X Y 总计
3 6 9
m 8
总计 14
A. B. C. D.
9.(多选)某中学为了解性别因素是否对本校学生体育锻炼的经常性有影响,从本校所有学生中随机调查了50名男生和50名女生,得到如下表格:
经常体育锻炼 不经常体育锻炼
男 40 10
女 30 20
附:,.
0.1 0.05 0.01
k 2.706 3.841 6.635
经计算,则可以推断出( )
A.该学校男生中经常体育锻炼的概率的估计值为
B.该学校女生中经常体育锻炼的概率的估计值为
C.有的把握认为男、女生在体育锻炼的经常性方面有差异
D.有的把握认为男、女生在体育锻炼的经常性方面有差异
10.(多选)为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法共抽取88名学生,通过测验判断其数学成绩是否优秀,得到了如下列联表:
学校 数学成绩 总计
不优秀 优秀
甲校 33 10 43
乙校 38 7 45
总计 71 17 88
已知,根据表中数据,计算得到.
0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
则下列说法正确的是( )
A.在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率没有差异
B.在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率有差异
C.若将表中所有数据都扩大为原来的10倍,在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率有差异
D.若将表中所有数据都扩大为原来的10倍,在犯错误的概率不超过0.001的前提下,可以认为两校的数学成绩优秀率没有差异
11.博鳌亚洲论坛2022年年会于4月20日至4月22日在海南博鳌镇举行.为了搞好对外宣传工作,会务组选聘了50名记者负责对外翻译工作,在下面“性别与会俄语”的列联表中,___________.
会俄语 不会俄语 总计
男 a b 20
女 6 d
总计 18 50
12.为了判断高二年级学生是否选修文科与性别的关系,现随机抽取50名高二年级学生,得到如下列联表.
理科 文科
男 13 10
女 7 20
已知,.根据表中数据,得到,则认为学生选修文科与性别有关系出错的可能性为___________.
13.有两个分类变量x和y,其中一组观测值为如表所示的列联表:
总计
a 15
50
总计 20 45 65
其中a,均为大于5的整数,则_________时,在犯错误的概率不超过0.01的前提下可以认为“x和y之间有关系”.
附:.
0.10 0.05 0.010 0.005
k 2.706 3.841 6.635 7.879
14.新疆某农科所为了研究不同土壤环境下棉花的品质,选取了甲、乙两块试验田进行种植.在棉花成熟后采摘,分别从甲、乙两块试验田采摘的棉花中各随机抽取50份样本,测定其马克隆值,整理测量数据得到如下列联表(单位:份),其中且.
注:棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标,是棉花纤维重要的内在质量指标之一.根据国家标准规定,马克隆值可分为A,B,C三个级别,A级品质最好,B级品质为标准,C级品质最差.
A级或B级 C级 合计
甲试验田 a 50
乙试验田 50
合计 80 20 100
当时,有的把握认为该品种棉花的马克隆值级别与土壤环境有关,则的最小值为____________.
附:,其中.
0.05 0.010 0.001
3.841 6.635 10.828
15.为响应国家使用新能源的号召,促进“碳达峰、碳中和”的目标实现,某汽车生产企业在积极上市四款新能源汽车后,对它们进行了市场调研.该企业研发部门从购买这四款车的车主中随机抽取了50人,让车主对所购汽车的性能进行评分,每款车的性能都有1分、2分、3分、4分、5分五个等级,各款车的评分及相应人数的统计结果如下表.
汽车款式 性能评分
1 2 3 4 5
基础版 基础版1 2 2 3 1 0
基础版2 4 4 5 3 1
豪华版 豪华版1 1 3 5 4 1
豪华版2 0 0 3 5 3
(1)求所抽车主对这四款车性能评分的平均数和分位数.
(2)当评分不小于4时,认为该款车性能优秀,否则认为性能一般.根据上述样本数据,完成以下列联表,那么在犯错误的概率不超过0.05的前提下,能否认为汽车的性能与款式有关?并解释所得结论的实际含义.
汽车性能 汽车款式 总计
基础版 豪华版
一般
优秀
总计
附:,.
0.10 0.05 0.01 0.005
k 2.706 3.841 6.635 7.879
答案以及解析
1.答案:C
解析:因为,所以有的把握认为两个变量有关系.故选C.
2.答案:C
解析:计算得,经查对临界值表知,
有的把握说患肺病与吸烟有关,故选C.
3.答案:C
解析:按照独立性检验的知识及比对的参数值,当,我们可以下结论变量x与变量y独立.故排除选项A,B;依据的独立性检验,,所以我们不能得到“变量x与变量y独立,这个结论犯错误的概率不超过0.01”这个结论.故C正确,D错误.故选C.
4.答案:D
解析:,有的把握认为“数学成绩优秀与性别有关”,即在犯错误的概率不超过的前提下认为“数学成绩优秀与性别有关”.所以ABC错误,故选D.
5.答案:A
解析:因为,所以有的把握认为学生的学习积极性与对待班级工作的态度有关系,故选A.
6.答案:C
解析:根据公式,得,
又且,,求得当或9时满足题意.故选C.
7.答案:D
解析:.
选项A,因为,所以有以上的把握认为“性别与是否喜欢阅读有关”,故A错误;
选项B,因为,所以没有以上的把握认为“性别与是否喜欢阅读有关”,故B错误;
选项C,因为,所以在犯错误的概率不超过0.025的前提下,不能认为“性别与是否喜欢阅读有关”,故C错误;
选项D,因为,所以在犯错误的概率不超过0.05的前提下认为“性别与是否喜欢阅读有关”,故D正确.故选D.
8.答案:D
解析:由给定的列联表,
对于A,,,
对于B,,,
对于C,,,
对于D,,,
显然0.2086最大,因此选项D中数据求得最大,说明X与Y有关联的可能性最大.故选D.
9.答案:BC
解析:选项A,该学校男生中经常体育锻炼的概率的估计值为,A错误;
选项B,女生中经常体育锻炼的概率的估计值为,B正确.
选项C,,故有的把握认为男、女生在体育锻炼的经常性方面有差异,C正确.
选项D,,故没有的把握认为男、女生在体育锻炼的经常性方面有差异,D错误.故选BC.
10.答案:ACD
解析:由题意可知,所以在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率没有差异,故选项A正确,选项B错误;
若将表中所有数据都扩大为原来的10倍,则,所以在犯错误的概率不超过0.1的前提下,可以认为两校的数学成绩优秀率有差异,故选项C正确;
若将表中所有数据都扩大为原来的10倍,则,所以在犯错误的概率不超过0.001的前提下,可以认为两校的数学成绩优秀率没有差异,故选项D正确,故选ACD.
11.答案:28
解析:由题得解得所以.
12.答案:
解析:,且,
认为学生选修文科与性别有关系出错的可能性为.
13.答案:9
解析:由题意知,
则,
解得或,因为且,,
所以,,所以.
14.答案:46
解析:依题意,得,
故,
整理,得,即,
因为且,
所以,所以,
又,所以的最小值为46.
15.答案:(1)平均数为3,分位数为4.5
(2)列联表中见解析;在犯错误的概率不超过0.05的前提下,认为汽车性能与款式有关;含义见解析
解析:(1)由题意得这四款车性能评分的平均数为
.
由知其分位数为.
(2)由题意得列联表如下所示:
汽车性能 汽车款式 总计
基础版 豪华版
一般 20 12 32
优秀 5 13 18
总计 25 25 50
根据列联表中的数据,经计算得到.
所以在犯错误的概率不超过0.05的前提下,认为汽车性能与款式有关.
汽车性能一般中,基础版和豪华版的频率分别为和;
汽车性能优秀中,基础版和豪华版的频率分别为和,
根据频率稳定于概率的原理,可以认为性能优秀时豪华版的概率大.
