初中数学湘教版九年级下册1.2.3二次函数y=a(x-h)2+k的图象与性质 教案
文档属性
| 名称 | 初中数学湘教版九年级下册1.2.3二次函数y=a(x-h)2+k的图象与性质 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 84.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览


文档简介
1.2 二次函数的图象与性质
第3课时
1.理解y=a(x-h)2+k的图象与y=a(x-h)2的图象的关系.
2.掌握二次函数y=a(x-h)2+k的图象与性质.
3.会用描点法画出y=a(x-h)2+k的图象.
4.经历探索二次函数y=a(x-h)2+k的图象的作法和性质的过程,进一步领会数形结合的思想,培养观察、分析、总结的能力.
重点:会画二次函数y=a(x-h)2+k的图象,掌握它的性质.
难点:理解y=a(x-h)2+k的图象与y=a(x-h)2的图象的关系.
一、复习
1.y=ax2(a≠0),y=a(x-h)2(a≠0)的图象的开口方向、对称轴、顶点坐标,y随x的增减性分别是什么
2.如何由y=ax2(a≠0)的图象平移得到y=a(x-h)2(a≠0)的图象
3.猜想二次函数y=a(x-h)2+k(a≠0)的图象开口方向、对称轴、顶点坐标及y随x的增减性如何
二、探索归纳
1.探索y=a(x-h)2+k的图象
问题:如何画二次函数y=(x-1)2+3的图象
学生填空:
我们来探究二次函数y=(x-1)2+3与y=(x-1)2之间的关系.
二次函数 图象上的点
横坐标x 纵坐标y
y=(x-1)2 a (a-1)2
y=(x-1)2+3 a (a-1)2+3
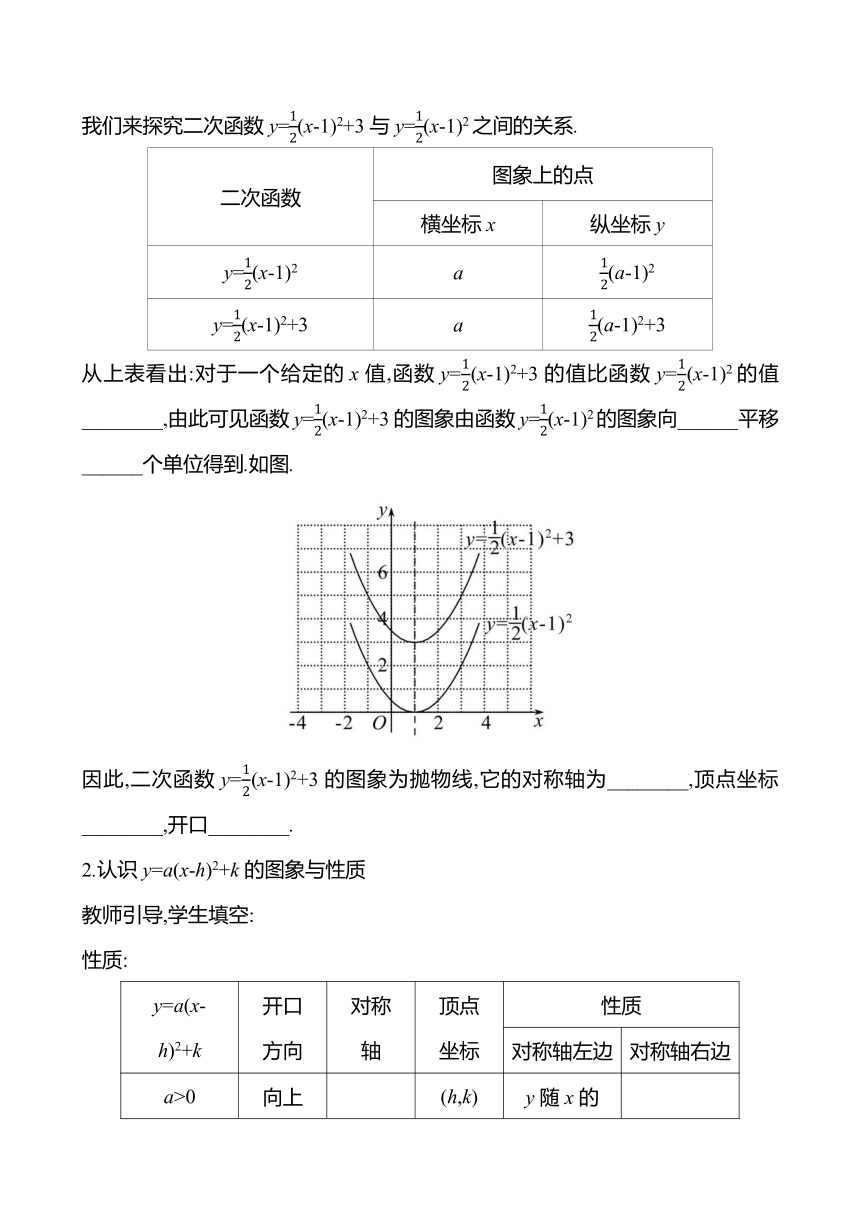
从上表看出:对于一个给定的x值,函数y=(x-1)2+3的值比函数y=(x-1)2的值________,由此可见函数y=(x-1)2+3的图象由函数y=(x-1)2的图象向______平移______个单位得到.如图.
因此,二次函数y=(x-1)2+3的图象为抛物线,它的对称轴为________,顶点坐标________,开口________.
2.认识y=a(x-h)2+k的图象与性质
教师引导,学生填空:
性质:
y=a(x- h)2+k 开口 方向 对称 轴 顶点 坐标 性质
对称轴左边 对称轴右边
a>0 向上 (h,k) y随x的 增大而减小
a<0 x=h y随x的 增大而减小
画y=a(x-h)2+k的图象的一般步骤.
(1)先写出对称轴和顶点坐标,并且在平面直角坐标系内画出________,再描出________;
(2)列表(自变量x从顶点的横坐标开始取值),描点和连线,画出图象在对称轴________的部分;
(3)利用________,画出图象在对称轴左边的部分(这只要先把对称轴左边的对应点描出来,然后用一条光滑曲线顺次连接它们和顶点).
3.y=a(x-h)2+k图象与性质的应用
例1:画二次函数y=(x+1)2-3的图象.
师生活动:
1.教师引导,学生填空,完成下列问题:
对称轴是直线________,顶点坐标为________.
列表:自变量x从________开始取值.
x … -2 -1 0 1 2 3 …
y=(x +1)2-3 … __ -3 __ -1 __ __ …
描点和连线:画出图象在对称轴右边的部分.利用对称性,画出图象在对称轴左边的部分.
2.学生画二次函数y=(x+1)2-3的图象
例2:已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.
师生活动:教师出示下列问题,学生解答.
1.抛物线的顶点坐标为(-2,1),可以设二次函数的表达式是什么
2.点(0,4)在抛物线上,点的坐标与抛物线的关系式有什么关系
3.学生写出解题过程.
解:因为抛物线的顶点坐标为(-2,1),
所以设这个抛物线所表示的二次函数的表达式为y=a(x+2)2+1.
由函数图象经过点(0,4),可得4=a (0+2)2+1,解得:a=.
因此,所求的二次函数的表达式为y=(x+2)2+1=x2+3x+4.
三、交流反思
1.二次函数y=a(x-h)2+k的图象是抛物线,它的对称轴是直线x=h,它的顶点坐标是(h,k).当a>0时,抛物线的开口向上;当a<0时,开口向下.
2.抛物线y=a(x-h)2+k是由y=a(x-h)2沿y轴方向上、下平移|k|个单位得到的,当k>0时, 向上平移,当k<0时,向下平移.
四、检测反馈
1.若抛物线y=-7(x+4)2-1平移得到y=-7x2,则必须( )
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向上平移4个单位
2.抛物线y=-3(x+2)2-4的顶点坐标是________,当x________时,函数值y随x的增大而增大.
3.若抛物线的对称轴为x=-1,与x轴的一个交点坐标为(1,0),则这条抛物线与x轴的另一个交点坐标是________.
4.已知二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到抛物线y=-(x+1)2+3.
(1)试确定a,h,k的值.
(2)指出二次函数y=a(x-h)2+k图象的开口方向,对称轴和顶点坐标.
五、布置作业
课本P15 第2,3题.
六、板书设计
1.2 二次函数的图象与性质 第3课时
问题 图象与性质 例
…… …… ……
…… …… ……
七、教学反思
通过本节学习使学生掌握画二次函数y=a(x-h)2+k的图象的方法:先确定顶点、对称轴以及开口方向,然后利用列表、描点、连线画y=a(x-h)2+k图象的一部分,然后利用对称性画出另一部分.
优点:通过本节的学习培养了学生的观察能力和抽象概括能力,渗透了数形结合的思想.
缺点:课堂容量稍有点偏大,学生没有时间独立完成作业.虽然我对每个问题及时小结、归纳,但没有留一定时间让学生整理消化.
第3课时
1.理解y=a(x-h)2+k的图象与y=a(x-h)2的图象的关系.
2.掌握二次函数y=a(x-h)2+k的图象与性质.
3.会用描点法画出y=a(x-h)2+k的图象.
4.经历探索二次函数y=a(x-h)2+k的图象的作法和性质的过程,进一步领会数形结合的思想,培养观察、分析、总结的能力.
重点:会画二次函数y=a(x-h)2+k的图象,掌握它的性质.
难点:理解y=a(x-h)2+k的图象与y=a(x-h)2的图象的关系.
一、复习
1.y=ax2(a≠0),y=a(x-h)2(a≠0)的图象的开口方向、对称轴、顶点坐标,y随x的增减性分别是什么
2.如何由y=ax2(a≠0)的图象平移得到y=a(x-h)2(a≠0)的图象
3.猜想二次函数y=a(x-h)2+k(a≠0)的图象开口方向、对称轴、顶点坐标及y随x的增减性如何
二、探索归纳
1.探索y=a(x-h)2+k的图象
问题:如何画二次函数y=(x-1)2+3的图象
学生填空:
我们来探究二次函数y=(x-1)2+3与y=(x-1)2之间的关系.
二次函数 图象上的点
横坐标x 纵坐标y
y=(x-1)2 a (a-1)2
y=(x-1)2+3 a (a-1)2+3
从上表看出:对于一个给定的x值,函数y=(x-1)2+3的值比函数y=(x-1)2的值________,由此可见函数y=(x-1)2+3的图象由函数y=(x-1)2的图象向______平移______个单位得到.如图.
因此,二次函数y=(x-1)2+3的图象为抛物线,它的对称轴为________,顶点坐标________,开口________.
2.认识y=a(x-h)2+k的图象与性质
教师引导,学生填空:
性质:
y=a(x- h)2+k 开口 方向 对称 轴 顶点 坐标 性质
对称轴左边 对称轴右边
a>0 向上 (h,k) y随x的 增大而减小
a<0 x=h y随x的 增大而减小
画y=a(x-h)2+k的图象的一般步骤.
(1)先写出对称轴和顶点坐标,并且在平面直角坐标系内画出________,再描出________;
(2)列表(自变量x从顶点的横坐标开始取值),描点和连线,画出图象在对称轴________的部分;
(3)利用________,画出图象在对称轴左边的部分(这只要先把对称轴左边的对应点描出来,然后用一条光滑曲线顺次连接它们和顶点).
3.y=a(x-h)2+k图象与性质的应用
例1:画二次函数y=(x+1)2-3的图象.
师生活动:
1.教师引导,学生填空,完成下列问题:
对称轴是直线________,顶点坐标为________.
列表:自变量x从________开始取值.
x … -2 -1 0 1 2 3 …
y=(x +1)2-3 … __ -3 __ -1 __ __ …
描点和连线:画出图象在对称轴右边的部分.利用对称性,画出图象在对称轴左边的部分.
2.学生画二次函数y=(x+1)2-3的图象
例2:已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.
师生活动:教师出示下列问题,学生解答.
1.抛物线的顶点坐标为(-2,1),可以设二次函数的表达式是什么
2.点(0,4)在抛物线上,点的坐标与抛物线的关系式有什么关系
3.学生写出解题过程.
解:因为抛物线的顶点坐标为(-2,1),
所以设这个抛物线所表示的二次函数的表达式为y=a(x+2)2+1.
由函数图象经过点(0,4),可得4=a (0+2)2+1,解得:a=.
因此,所求的二次函数的表达式为y=(x+2)2+1=x2+3x+4.
三、交流反思
1.二次函数y=a(x-h)2+k的图象是抛物线,它的对称轴是直线x=h,它的顶点坐标是(h,k).当a>0时,抛物线的开口向上;当a<0时,开口向下.
2.抛物线y=a(x-h)2+k是由y=a(x-h)2沿y轴方向上、下平移|k|个单位得到的,当k>0时, 向上平移,当k<0时,向下平移.
四、检测反馈
1.若抛物线y=-7(x+4)2-1平移得到y=-7x2,则必须( )
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向上平移4个单位
2.抛物线y=-3(x+2)2-4的顶点坐标是________,当x________时,函数值y随x的增大而增大.
3.若抛物线的对称轴为x=-1,与x轴的一个交点坐标为(1,0),则这条抛物线与x轴的另一个交点坐标是________.
4.已知二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到抛物线y=-(x+1)2+3.
(1)试确定a,h,k的值.
(2)指出二次函数y=a(x-h)2+k图象的开口方向,对称轴和顶点坐标.
五、布置作业
课本P15 第2,3题.
六、板书设计
1.2 二次函数的图象与性质 第3课时
问题 图象与性质 例
…… …… ……
…… …… ……
七、教学反思
通过本节学习使学生掌握画二次函数y=a(x-h)2+k的图象的方法:先确定顶点、对称轴以及开口方向,然后利用列表、描点、连线画y=a(x-h)2+k图象的一部分,然后利用对称性画出另一部分.
优点:通过本节的学习培养了学生的观察能力和抽象概括能力,渗透了数形结合的思想.
缺点:课堂容量稍有点偏大,学生没有时间独立完成作业.虽然我对每个问题及时小结、归纳,但没有留一定时间让学生整理消化.
