小升初应用题专项训练:图形与几何(含答案)-数学六年级下册人教版
文档属性
| 名称 | 小升初应用题专项训练:图形与几何(含答案)-数学六年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 693.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 17:49:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初应用题专项训练:图形与几何-数学六年级下册人教版
典型例题解析
1.下图是一个长方形的羊圈,羊圈的周围是草地。把一只羊拴在羊圈墙面外的拐角处(如图)。已知拴羊的绳子长2米。
(1)在图上画出这只羊能吃到草的范围并涂上阴影。
(2)这只羊能吃到的草的最大面积是多少平方米?
【答案】(1)见详解;
(2)9.42平方米
【分析】(1)这只羊能吃到草的范围是以2米长为半径的圆面积的,据此画图即可;
(2)这只羊能吃到草的最大面积是以2米长为半径的圆面积的,根据圆的面积公式S=解答即可。
【详解】
(1)如图:
(2)3.14××
=3.14×4×
=12.56×
=9.42(平方米)
答:这只羊能吃到的草的最大面积是9.42平方米。
2.如图,一个实心圆柱形铁块的高是10cm,如果把它切割成两个相同的半圆柱,表面积就增加了160cm2,如果把这个圆柱锻造成一个底面半径是5cm的实心圆锥形铅锤,这个铅锤的高是多少cm?
【答案】19.2cm
【分析】增加的面积是以圆柱形铁块的高为长、圆柱的底面直径为宽的两个长方形的面积,据此用160除以2,求出一个长方形的面积,再用一个长方形的面积除以圆柱形铁块的高就是底面直径,再除以2就是圆柱形铁块的底面半径,再根据圆柱的体积=求出圆柱形铁块的体积,也就是半径是5cm的实心圆锥形铅锤的体积,再根据圆锥的高=圆锥体积的3倍÷底面积解答即可。
【详解】160÷2÷10÷2
=80÷10÷2
=8÷2
=4(cm)
=16×10×3÷25
=160×3÷25
=480÷25
=19.2(cm)
答:这个铅锤的商是19.2cm。
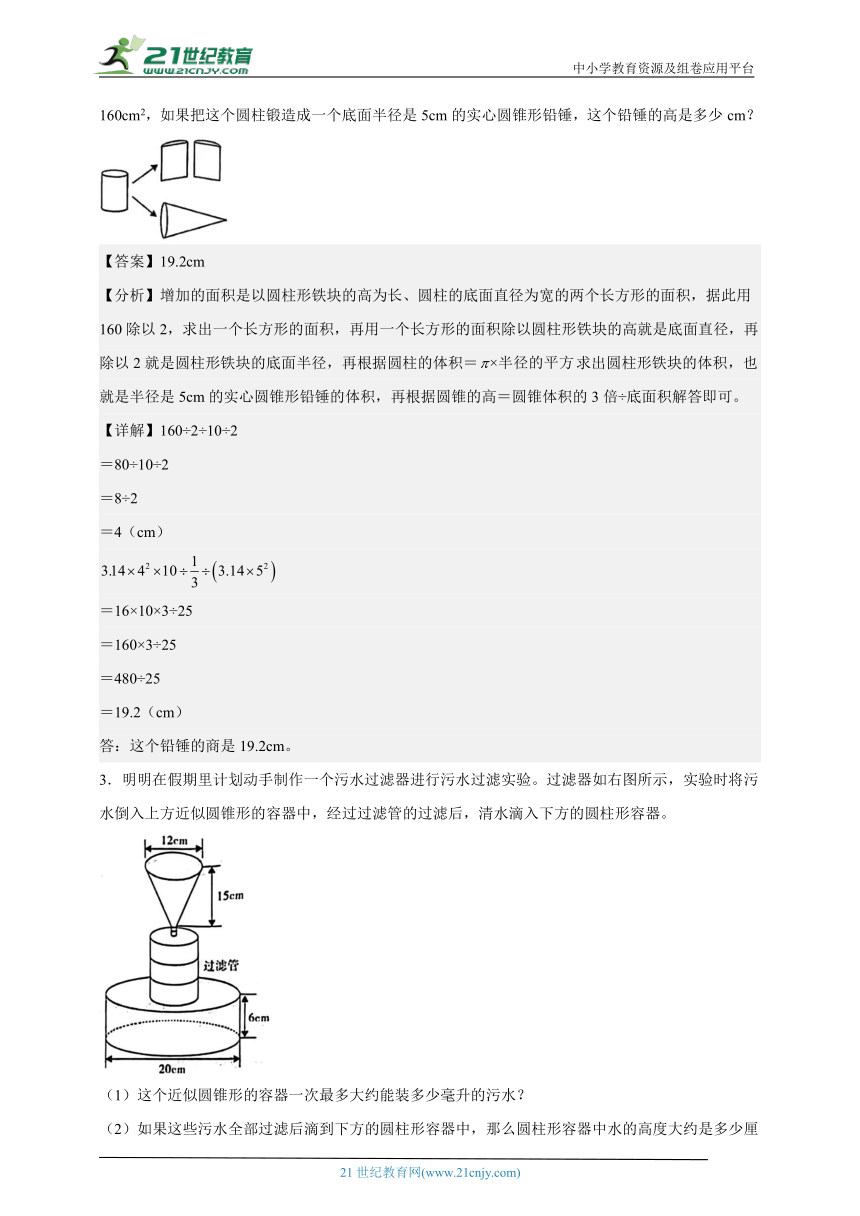
3.明明在假期里计划动手制作一个污水过滤器进行污水过滤实验。过滤器如右图所示,实验时将污水倒入上方近似圆锥形的容器中,经过过滤管的过滤后,清水滴入下方的圆柱形容器。
(1)这个近似圆锥形的容器一次最多大约能装多少毫升的污水?
(2)如果这些污水全部过滤后滴到下方的圆柱形容器中,那么圆柱形容器中水的高度大约是多少厘米(不考虑过滤掉的杂质体积)?
【答案】(1)565.2毫升;(2)5厘米
【分析】(1)求圆锥形容器一次能装入多少毫升的污水,就是求一个底面直径是12厘米,高15厘米的圆锥的体积,利用圆锥的体积=πr2h求解即可。
(2)因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【详解】(1)3.14×(12÷2)2×15×
=3.14×62×15×
=3.14×36×15×
=113.04×15×
=1695.6×
=565.2(立方厘米)
565.2立方厘米=565.2毫升
答:这个近似圆锥形的容器一次最多大约能装565.2毫升的污水。
(2)15×=5(厘米)
答:圆柱形容器中水的高度大约是5厘米。
强化训练
1.一台压路机的前轮半径是0.5米,如果前轮每分转动8周,10分可以从路的一端转到另一端,这条路约长多少米?
2.张大爷用竹篱笆靠墙围了一个半圆形的小花园,篱笆的长度约为6.28m,你知道围在花园里的墙的长度约是多少m吗?
3.将一个圆沿半径剪开,得到若干个大小相同的小扇形,然后拼成一个近似的长方形,如果拼成的长方形长9.42分米,那么原来圆的面积是多少平方分米?
4.有一根长5厘米的分针,当它经过45分钟后,它扫过的面积是多少?分针尖端经过的距离是多少?
5.如图,正方形的边长是2厘米,四个圆的圆心分别是正方形的顶点。正方形中被圆盖住的面积是多少平方厘米?
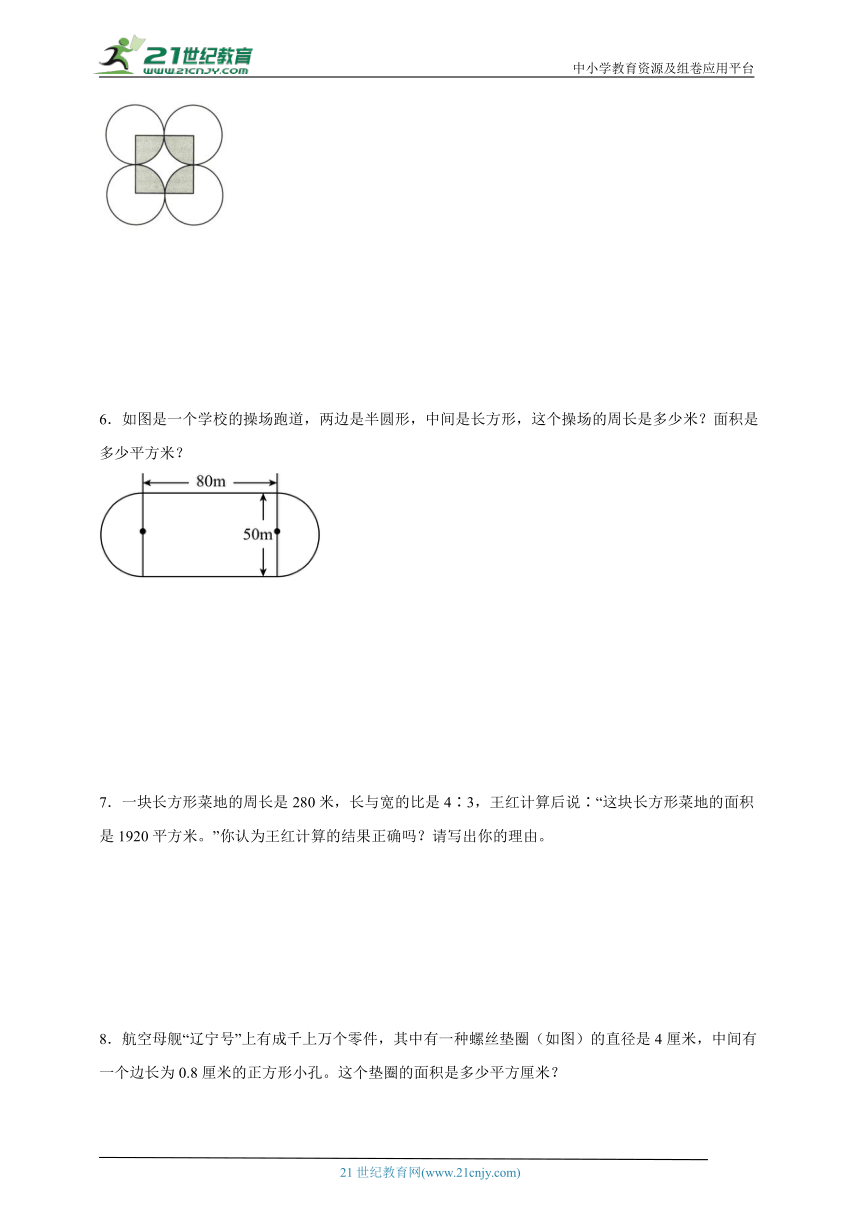
6.如图是一个学校的操场跑道,两边是半圆形,中间是长方形,这个操场的周长是多少米?面积是多少平方米?
7.一块长方形菜地的周长是280米,长与宽的比是4∶3,王红计算后说∶“这块长方形菜地的面积是1920平方米。”你认为王红计算的结果正确吗?请写出你的理由。
8.航空母舰“辽宁号”上有成千上万个零件,其中有一种螺丝垫圈(如图)的直径是4厘米,中间有一个边长为0.8厘米的正方形小孔。这个垫圈的面积是多少平方厘米?
9.如图,四边形被分成四个三角形,四边形的面积是42平方厘米,其中两个小三角形的面积分别是3平方厘米和4平方厘米,那么最大的一个三角形的面积是多少平方厘米?
10.在比例尺是1∶1000的学校平面图上,量得长方形操场的长是10厘米,宽是5厘米。这个操场的实际面积是多少平方米?
11.一块梯形稻田,中间有一条水渠通道。
(1)实际种植水稻的面积是多少平方米?
(2)如果每平方米稻田产水稻1.2千克,那么这块稻田共产水稻多少千克?
12.有A、B两个容器(如图所示,单位:cm)。先把容器A装满水,然后把水全部倒入容器B中水的高度多少?
13.把一个圆柱体经过底面直径,沿着它的高线切开,切面是一个边长是5厘米的正方形。这个圆柱体的侧面积是多少?
14.如图中圆柱的底面周长是25.12cm,高是15dm,现用包装绳包扎,至少需要多长的包装绳?(接头处需15cm)
15.已知圆的周长是25.12厘米,四边形OABC是一个直角梯形,OA∶CB=2∶5,图中阴影部分的面积是多少平方厘米?(解答题,写出主要解答步骤)。
16.一堆9.8方的沙子装入到一个高1.8米的圆柱形容器里,露出的部分是一个高0.9米的圆锥形沙堆,这个圆锥形沙堆的体积是多少立方米?(1方等于1立方米)
17.将一块底面积为0.5平方米、高6分米的长方体铁块熔铸成底面积为8平方分米的圆锥,圆锥的高是多少米?
18.一个密封的长方体容器装了一些水。当横着放入一个圆柱体铁块时,恰好完全浸没在水中,水深2厘米(如下左图)。如果把这个容器如下右图放置,圆柱体铁块的刚好露出水面,且水深5.5厘米。
(1)当把这个容器如下右图放置时,占地面积是多少?
(2)这个圆柱体铁块的体积是多少立方厘米?
参考答案:
1.251.2米
【分析】压路机的前轮侧面是一个圆形,先根据“C=2πr”来求出压路机的前轮侧面周长,也就是前轮转一圈压过路面的长度,然后用侧面周长乘上前轮每分转动的周数,求出积,最后乘上压路的时间,求出积,即可解决。
【详解】2×3.14×0.5
=6.28×0.5
=3.14(米)
3.14×8×10
=25.12×10
=251.2(米)
答:这条路约长251.2米。
2.4m
【分析】用竹篱笆靠墙围了一个半圆形的小花园,篱笆的长度约为6.28m,墙不用围,所以篱笆的长度就是圆周长的一半,用圆周长的一半乘2,求出积就是圆的周长,然后根据“d=C÷π”来求出直径,也就是花园里的墙的长度。
【详解】6.28×2÷3.14
=12.56÷3.14
=4(m)
答:花园里的墙的长度约是4m。
3.28.26平方分米
【分析】将一个圆沿半径剪开拼成一个近似的长方形,拼成的长方形的长是圆周长的一半,用圆周长的一半乘2,求出圆周长,根据公式:半径=圆周长÷圆周率÷2,求出圆的半径,在根据面积公式:圆的面积=圆周率×半径的平方,即可求出原来圆的面积是多少,据此解答。
【详解】9.42×2=18.82(分米)
18.84÷3.14÷2=3(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:原来圆的面积是28.26平方分米。
4.58.875平方厘米;23.55厘米
【分析】1小时=60分钟,用45÷60,求出45分钟是60分钟的几分之几;即45÷60=;根据圆的面积公式:面积=π×半径2,代入数据,求出半径等于长5厘米的钟的面积,再乘,即可求出扫过的面积;再根据圆的周长公式:周长=π×半径×2,代入数据,求出半径等于长5厘米的钟的周长,再乘,即可求出分针尖端经过的距离,据此解答。
【详解】45÷60=
3.14×52×
=3.14×25×
=78.5×
=58.578(平方厘米)
3.14×5×2×
=15.7×2×
=31.4×
=23.55(厘米)
答:它扫过的面积是58.578平方厘米,分针尖端经过的距离是23.55厘米。
5.3.14平方厘米
【分析】根据题意可知,正方形中被圆盖住的面积就是一个半径是(2÷2)厘米的圆的面积,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14(平方厘米)
答:方形中被圆盖住的面积是3.14平方厘米。
6.317米;5962.5平方米
【分析】观察图形可知,操场跑道两端的两个半圆可以组合成一个直径为50米圆。
这个操场的周长=圆的周长+2条80米的直道,根据圆的周长公式C=πd,代入数据计算,求出这个操场的周长。
这个操场的面积=圆的面积+长方形的面积,根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算,求出这个操场的面积。
【详解】操场的周长:
3.14×50+80×2
=157+160
=317(米)
操场的面积:
3.14×(50÷2)2+80×50
=3.14×252+4000
=3.14×625+4000
=1962.5+4000
=5962.5(平方米)
答:这个操场的周长是317米,面积是5962.5平方米。
7.不正确;理由见详解
【分析】已知周长是280米,则长+宽=280÷2=140(米);长与宽的比是4∶3,则长是长与宽的和的,宽是是长与宽的和的,先用乘法算出长和宽分别是多少,再根据长方形的面积=长×宽,代入数据计算,即可求出这块长方形菜地的面积是多少,据此解答。
【详解】280÷2=140(米)
140×
=140×
=80(米)
140×
=140×
=60(米)
60×80=4800(平方米)
1920平方米≠4800平方米
答:这块长方形菜地的面积是4800平方米,所以王红计算的结果不正确。
8.11.92平方厘米
【分析】由图可知,这个垫圈的面积等于圆的面积减去中间正方形的面积,根据公式:S=a×a=a ,S=πr ,r=d÷2,代入数据计算即可解答。
【详解】
(平方厘米)
答:这个垫圈的面积是11.92平方厘米。
9.20平方厘米
【分析】和等高,所以DE∶EB=∶=3∶4。同理和等高,所以∶=DE∶EB=3∶4。先用四边形面积减去两个小三角形的面积得到和的面积和,再根据∶=3∶4,那么和分别是把面积和平均分成3+4=7份中的3份和4份,求出一份的面积再乘最大的份数即可找出最大的三角形面积。
【详解】因为,并且和等高,所以DE∶EB=∶=3∶4。
因为和等高,所以∶=DE∶EB=3∶4。
因为+=42-3-4=35(平方厘米)
所以(平方厘米)
=35-15=20(平方厘米)
因为3<4<15<20,所以最大的一个三角形的面积是20平方厘米。
答:最大的一个三角形的面积是20平方厘米。
【点睛】本题考查对三角形高的认识、三角形面积的灵活计算及按比分配问题。
10.5000平方米
【分析】根据关系式:实际距离=图上距离÷比例尺,即可求得长和宽的实际距离各是多少,再根据长方形的面积=长×宽,即可求解。
【详解】10÷
=10×1000
=10000(厘米)
5÷
=5×1000
=5000(厘米)
10000厘米=100米
5000厘米=50米
100×50=5000(平方米)
答:这个操场的实际面积是5000平方米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
11.(1)934.5平方米
(2)1121.4千克
【分析】先求梯形的面积,在求面积的时候上底和下底要把小路的宽减去,然后再根据梯形的面积=(上底+下底)×高÷2;
用梯形的面积乘1.2就是求的这块稻田的产量。
【详解】(1)(44-1.5+48-1.5)×21÷2
=89×10.5
=934.5(平方米)
答:实际种植水稻的面积是934.5平方米。
(2)1.2×934.5=1121.4(千克)
答:这块稻田共产水稻1121.4千克。
【点睛】注意求梯形面积的时候要减去小路的面积。
12.1.2厘米
【分析】先利用圆锥的容积公式:圆锥体积=×底面积×高求出水的体积,再把这些水倒入圆柱容器中,利用圆柱的体积公式:圆柱体积=底面积×高求出水的高度。
【详解】(×3.14×32×10)÷[3.14×(10÷2)2]
=(×3.14×9×10)÷(3.14×25)
=30÷25
=1.2(厘米)
答:这时容器B中水的高度是1.2厘米。
【点睛】此题考查了圆锥与圆柱的体积公式的灵活应用。
13.78.5平方厘米
【分析】根据题意可知,把这个圆柱沿底面直径和高切开,切面是一个正方形,那么这个圆柱的底面直径和高相等,根据圆柱的侧面积公式:S=πdh,把数据代入公式解答。
【详解】3.14×5×5
=15.7×5
=78.5(平方厘米)
这个圆柱的侧面积是78.5平方厘米。
【点睛】此题主要考查圆柱侧面积公式的灵活运用,关键是熟记公式。
14.647厘米
【分析】根据题意和图形可知,所需彩带的长度等于4条高,4条直径,再加打结处用的15厘米,由此列式解答。
【详解】15分米=150厘米
底面直径:
25.12÷3.14=8(厘米)
8×4+150×4+15
=32+600+15
=647(厘米)
答:至少需要647厘米的包装绳。
【点睛】此题属于圆柱体知识的实际应用,解答关键是弄清是如何捆扎的,也就是弄清是求哪些数据的长度和。
15.15.44平方厘米
【分析】先根据r=C÷π÷2,求出圆的半径,也是梯形的上底OA和梯形的高OC的长度;已知OA∶CB=2∶5,即OA占2份,CB占5份,用OA的长度除以2再乘5,即可求出CB的长度;
从图中可知,阴影部分的面积=梯形的面积-圆的面积,其中梯形的面积=(上底+下底)×高÷2,圆的面积公式S=πr2,代入数据计算即可。
【详解】圆的半径(OA、OC):
25.12÷3.14÷2
=8÷2
=4(厘米)
梯形的下底CB:
4÷2×5
=2×5
=10(厘米)
梯形的面积:
(4+10)×4÷2
=14×4÷2
=56÷2
=28(平方厘米)
圆的面积:
×3.14×42
=×3.14×16
=12.56(平方厘米)
阴影部分的面积:
28-12.56=15.44(平方厘米)
答:阴影部分的面积是15.44平方厘米。
【点睛】本题考查圆的面积、梯形的面积公式的灵活运用,根据圆的周长公式求出圆的半径,根据比的应用,求出梯形的下底CB是解题的关键。
16.1.4立方米
【分析】观察图形,圆锥的底面积和圆柱的底面积相等,可设为,利用圆柱的体积公式:V=,h=1.8米,代入表示出圆柱的体积,利用圆锥的体积公式:V=,h=0.9米,代入表示出圆锥的体积,圆柱的体积+圆锥的体积=9.8,求出,再通过圆锥的体积公式求出这个圆锥形沙堆的体积。
【详解】
由可得:
(立方米)
答:圆锥形沙堆的体积是1.4立方米。
【点睛】此题的解理关键是认识到圆柱和圆锥的底面积相等并通过体积公式求出底面积,再根据圆锥的体积公式即可得解。
17.11.25米
【分析】根据长方体体积=底面积×高,可求出长方体铁块的体积,把长方体铁块熔铸成圆锥,体积不变,已知圆锥的底面积,则根据圆锥的高=3×圆锥的体积÷底面积即可得圆锥的高是多少米。
【详解】6分米=0.6米
0.5×0.6=0.3(立方米)
8平方分米=0.08平方米
3×0.3÷0.08
=0.9÷0.08
=11.25(米)
答:圆锥的高是11.25米。
【点睛】本题主要考查了长方体体积公式和圆锥体积公式的灵活应用,注意计算时要先统一单位。
18.(1)20平方厘米
(2)40立方厘米
【分析】(1)占地面积指的是底面积,根据长方形面积=长×宽,列式解答即可。
(2)圆柱露出水面的体积=第一个图长×宽×水深-第二个图长×宽×水深,将圆柱体积看作单位“1”,露出水面的体积÷对应分率=圆柱体积,据此列式解答。
【详解】(1)5×4=20(平方厘米)
答:占地面积是20平方厘米。
(2)12×5×2-5×4×5.5
=120-110
=10(立方厘米)
10÷=40(立方厘米)
答:这个圆柱体铁块的体积是40立方厘米。
【点睛】关键是掌握并灵活运用长方体表面积和体积公式,理解分数除法的意义。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初应用题专项训练:图形与几何-数学六年级下册人教版
典型例题解析
1.下图是一个长方形的羊圈,羊圈的周围是草地。把一只羊拴在羊圈墙面外的拐角处(如图)。已知拴羊的绳子长2米。
(1)在图上画出这只羊能吃到草的范围并涂上阴影。
(2)这只羊能吃到的草的最大面积是多少平方米?
【答案】(1)见详解;
(2)9.42平方米
【分析】(1)这只羊能吃到草的范围是以2米长为半径的圆面积的,据此画图即可;
(2)这只羊能吃到草的最大面积是以2米长为半径的圆面积的,根据圆的面积公式S=解答即可。
【详解】
(1)如图:
(2)3.14××
=3.14×4×
=12.56×
=9.42(平方米)
答:这只羊能吃到的草的最大面积是9.42平方米。
2.如图,一个实心圆柱形铁块的高是10cm,如果把它切割成两个相同的半圆柱,表面积就增加了160cm2,如果把这个圆柱锻造成一个底面半径是5cm的实心圆锥形铅锤,这个铅锤的高是多少cm?
【答案】19.2cm
【分析】增加的面积是以圆柱形铁块的高为长、圆柱的底面直径为宽的两个长方形的面积,据此用160除以2,求出一个长方形的面积,再用一个长方形的面积除以圆柱形铁块的高就是底面直径,再除以2就是圆柱形铁块的底面半径,再根据圆柱的体积=求出圆柱形铁块的体积,也就是半径是5cm的实心圆锥形铅锤的体积,再根据圆锥的高=圆锥体积的3倍÷底面积解答即可。
【详解】160÷2÷10÷2
=80÷10÷2
=8÷2
=4(cm)
=16×10×3÷25
=160×3÷25
=480÷25
=19.2(cm)
答:这个铅锤的商是19.2cm。
3.明明在假期里计划动手制作一个污水过滤器进行污水过滤实验。过滤器如右图所示,实验时将污水倒入上方近似圆锥形的容器中,经过过滤管的过滤后,清水滴入下方的圆柱形容器。
(1)这个近似圆锥形的容器一次最多大约能装多少毫升的污水?
(2)如果这些污水全部过滤后滴到下方的圆柱形容器中,那么圆柱形容器中水的高度大约是多少厘米(不考虑过滤掉的杂质体积)?
【答案】(1)565.2毫升;(2)5厘米
【分析】(1)求圆锥形容器一次能装入多少毫升的污水,就是求一个底面直径是12厘米,高15厘米的圆锥的体积,利用圆锥的体积=πr2h求解即可。
(2)因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此解答即可。
【详解】(1)3.14×(12÷2)2×15×
=3.14×62×15×
=3.14×36×15×
=113.04×15×
=1695.6×
=565.2(立方厘米)
565.2立方厘米=565.2毫升
答:这个近似圆锥形的容器一次最多大约能装565.2毫升的污水。
(2)15×=5(厘米)
答:圆柱形容器中水的高度大约是5厘米。
强化训练
1.一台压路机的前轮半径是0.5米,如果前轮每分转动8周,10分可以从路的一端转到另一端,这条路约长多少米?
2.张大爷用竹篱笆靠墙围了一个半圆形的小花园,篱笆的长度约为6.28m,你知道围在花园里的墙的长度约是多少m吗?
3.将一个圆沿半径剪开,得到若干个大小相同的小扇形,然后拼成一个近似的长方形,如果拼成的长方形长9.42分米,那么原来圆的面积是多少平方分米?
4.有一根长5厘米的分针,当它经过45分钟后,它扫过的面积是多少?分针尖端经过的距离是多少?
5.如图,正方形的边长是2厘米,四个圆的圆心分别是正方形的顶点。正方形中被圆盖住的面积是多少平方厘米?
6.如图是一个学校的操场跑道,两边是半圆形,中间是长方形,这个操场的周长是多少米?面积是多少平方米?
7.一块长方形菜地的周长是280米,长与宽的比是4∶3,王红计算后说∶“这块长方形菜地的面积是1920平方米。”你认为王红计算的结果正确吗?请写出你的理由。
8.航空母舰“辽宁号”上有成千上万个零件,其中有一种螺丝垫圈(如图)的直径是4厘米,中间有一个边长为0.8厘米的正方形小孔。这个垫圈的面积是多少平方厘米?
9.如图,四边形被分成四个三角形,四边形的面积是42平方厘米,其中两个小三角形的面积分别是3平方厘米和4平方厘米,那么最大的一个三角形的面积是多少平方厘米?
10.在比例尺是1∶1000的学校平面图上,量得长方形操场的长是10厘米,宽是5厘米。这个操场的实际面积是多少平方米?
11.一块梯形稻田,中间有一条水渠通道。
(1)实际种植水稻的面积是多少平方米?
(2)如果每平方米稻田产水稻1.2千克,那么这块稻田共产水稻多少千克?
12.有A、B两个容器(如图所示,单位:cm)。先把容器A装满水,然后把水全部倒入容器B中水的高度多少?
13.把一个圆柱体经过底面直径,沿着它的高线切开,切面是一个边长是5厘米的正方形。这个圆柱体的侧面积是多少?
14.如图中圆柱的底面周长是25.12cm,高是15dm,现用包装绳包扎,至少需要多长的包装绳?(接头处需15cm)
15.已知圆的周长是25.12厘米,四边形OABC是一个直角梯形,OA∶CB=2∶5,图中阴影部分的面积是多少平方厘米?(解答题,写出主要解答步骤)。
16.一堆9.8方的沙子装入到一个高1.8米的圆柱形容器里,露出的部分是一个高0.9米的圆锥形沙堆,这个圆锥形沙堆的体积是多少立方米?(1方等于1立方米)
17.将一块底面积为0.5平方米、高6分米的长方体铁块熔铸成底面积为8平方分米的圆锥,圆锥的高是多少米?
18.一个密封的长方体容器装了一些水。当横着放入一个圆柱体铁块时,恰好完全浸没在水中,水深2厘米(如下左图)。如果把这个容器如下右图放置,圆柱体铁块的刚好露出水面,且水深5.5厘米。
(1)当把这个容器如下右图放置时,占地面积是多少?
(2)这个圆柱体铁块的体积是多少立方厘米?
参考答案:
1.251.2米
【分析】压路机的前轮侧面是一个圆形,先根据“C=2πr”来求出压路机的前轮侧面周长,也就是前轮转一圈压过路面的长度,然后用侧面周长乘上前轮每分转动的周数,求出积,最后乘上压路的时间,求出积,即可解决。
【详解】2×3.14×0.5
=6.28×0.5
=3.14(米)
3.14×8×10
=25.12×10
=251.2(米)
答:这条路约长251.2米。
2.4m
【分析】用竹篱笆靠墙围了一个半圆形的小花园,篱笆的长度约为6.28m,墙不用围,所以篱笆的长度就是圆周长的一半,用圆周长的一半乘2,求出积就是圆的周长,然后根据“d=C÷π”来求出直径,也就是花园里的墙的长度。
【详解】6.28×2÷3.14
=12.56÷3.14
=4(m)
答:花园里的墙的长度约是4m。
3.28.26平方分米
【分析】将一个圆沿半径剪开拼成一个近似的长方形,拼成的长方形的长是圆周长的一半,用圆周长的一半乘2,求出圆周长,根据公式:半径=圆周长÷圆周率÷2,求出圆的半径,在根据面积公式:圆的面积=圆周率×半径的平方,即可求出原来圆的面积是多少,据此解答。
【详解】9.42×2=18.82(分米)
18.84÷3.14÷2=3(分米)
3.14×32
=3.14×9
=28.26(平方分米)
答:原来圆的面积是28.26平方分米。
4.58.875平方厘米;23.55厘米
【分析】1小时=60分钟,用45÷60,求出45分钟是60分钟的几分之几;即45÷60=;根据圆的面积公式:面积=π×半径2,代入数据,求出半径等于长5厘米的钟的面积,再乘,即可求出扫过的面积;再根据圆的周长公式:周长=π×半径×2,代入数据,求出半径等于长5厘米的钟的周长,再乘,即可求出分针尖端经过的距离,据此解答。
【详解】45÷60=
3.14×52×
=3.14×25×
=78.5×
=58.578(平方厘米)
3.14×5×2×
=15.7×2×
=31.4×
=23.55(厘米)
答:它扫过的面积是58.578平方厘米,分针尖端经过的距离是23.55厘米。
5.3.14平方厘米
【分析】根据题意可知,正方形中被圆盖住的面积就是一个半径是(2÷2)厘米的圆的面积,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14(平方厘米)
答:方形中被圆盖住的面积是3.14平方厘米。
6.317米;5962.5平方米
【分析】观察图形可知,操场跑道两端的两个半圆可以组合成一个直径为50米圆。
这个操场的周长=圆的周长+2条80米的直道,根据圆的周长公式C=πd,代入数据计算,求出这个操场的周长。
这个操场的面积=圆的面积+长方形的面积,根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算,求出这个操场的面积。
【详解】操场的周长:
3.14×50+80×2
=157+160
=317(米)
操场的面积:
3.14×(50÷2)2+80×50
=3.14×252+4000
=3.14×625+4000
=1962.5+4000
=5962.5(平方米)
答:这个操场的周长是317米,面积是5962.5平方米。
7.不正确;理由见详解
【分析】已知周长是280米,则长+宽=280÷2=140(米);长与宽的比是4∶3,则长是长与宽的和的,宽是是长与宽的和的,先用乘法算出长和宽分别是多少,再根据长方形的面积=长×宽,代入数据计算,即可求出这块长方形菜地的面积是多少,据此解答。
【详解】280÷2=140(米)
140×
=140×
=80(米)
140×
=140×
=60(米)
60×80=4800(平方米)
1920平方米≠4800平方米
答:这块长方形菜地的面积是4800平方米,所以王红计算的结果不正确。
8.11.92平方厘米
【分析】由图可知,这个垫圈的面积等于圆的面积减去中间正方形的面积,根据公式:S=a×a=a ,S=πr ,r=d÷2,代入数据计算即可解答。
【详解】
(平方厘米)
答:这个垫圈的面积是11.92平方厘米。
9.20平方厘米
【分析】和等高,所以DE∶EB=∶=3∶4。同理和等高,所以∶=DE∶EB=3∶4。先用四边形面积减去两个小三角形的面积得到和的面积和,再根据∶=3∶4,那么和分别是把面积和平均分成3+4=7份中的3份和4份,求出一份的面积再乘最大的份数即可找出最大的三角形面积。
【详解】因为,并且和等高,所以DE∶EB=∶=3∶4。
因为和等高,所以∶=DE∶EB=3∶4。
因为+=42-3-4=35(平方厘米)
所以(平方厘米)
=35-15=20(平方厘米)
因为3<4<15<20,所以最大的一个三角形的面积是20平方厘米。
答:最大的一个三角形的面积是20平方厘米。
【点睛】本题考查对三角形高的认识、三角形面积的灵活计算及按比分配问题。
10.5000平方米
【分析】根据关系式:实际距离=图上距离÷比例尺,即可求得长和宽的实际距离各是多少,再根据长方形的面积=长×宽,即可求解。
【详解】10÷
=10×1000
=10000(厘米)
5÷
=5×1000
=5000(厘米)
10000厘米=100米
5000厘米=50米
100×50=5000(平方米)
答:这个操场的实际面积是5000平方米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
11.(1)934.5平方米
(2)1121.4千克
【分析】先求梯形的面积,在求面积的时候上底和下底要把小路的宽减去,然后再根据梯形的面积=(上底+下底)×高÷2;
用梯形的面积乘1.2就是求的这块稻田的产量。
【详解】(1)(44-1.5+48-1.5)×21÷2
=89×10.5
=934.5(平方米)
答:实际种植水稻的面积是934.5平方米。
(2)1.2×934.5=1121.4(千克)
答:这块稻田共产水稻1121.4千克。
【点睛】注意求梯形面积的时候要减去小路的面积。
12.1.2厘米
【分析】先利用圆锥的容积公式:圆锥体积=×底面积×高求出水的体积,再把这些水倒入圆柱容器中,利用圆柱的体积公式:圆柱体积=底面积×高求出水的高度。
【详解】(×3.14×32×10)÷[3.14×(10÷2)2]
=(×3.14×9×10)÷(3.14×25)
=30÷25
=1.2(厘米)
答:这时容器B中水的高度是1.2厘米。
【点睛】此题考查了圆锥与圆柱的体积公式的灵活应用。
13.78.5平方厘米
【分析】根据题意可知,把这个圆柱沿底面直径和高切开,切面是一个正方形,那么这个圆柱的底面直径和高相等,根据圆柱的侧面积公式:S=πdh,把数据代入公式解答。
【详解】3.14×5×5
=15.7×5
=78.5(平方厘米)
这个圆柱的侧面积是78.5平方厘米。
【点睛】此题主要考查圆柱侧面积公式的灵活运用,关键是熟记公式。
14.647厘米
【分析】根据题意和图形可知,所需彩带的长度等于4条高,4条直径,再加打结处用的15厘米,由此列式解答。
【详解】15分米=150厘米
底面直径:
25.12÷3.14=8(厘米)
8×4+150×4+15
=32+600+15
=647(厘米)
答:至少需要647厘米的包装绳。
【点睛】此题属于圆柱体知识的实际应用,解答关键是弄清是如何捆扎的,也就是弄清是求哪些数据的长度和。
15.15.44平方厘米
【分析】先根据r=C÷π÷2,求出圆的半径,也是梯形的上底OA和梯形的高OC的长度;已知OA∶CB=2∶5,即OA占2份,CB占5份,用OA的长度除以2再乘5,即可求出CB的长度;
从图中可知,阴影部分的面积=梯形的面积-圆的面积,其中梯形的面积=(上底+下底)×高÷2,圆的面积公式S=πr2,代入数据计算即可。
【详解】圆的半径(OA、OC):
25.12÷3.14÷2
=8÷2
=4(厘米)
梯形的下底CB:
4÷2×5
=2×5
=10(厘米)
梯形的面积:
(4+10)×4÷2
=14×4÷2
=56÷2
=28(平方厘米)
圆的面积:
×3.14×42
=×3.14×16
=12.56(平方厘米)
阴影部分的面积:
28-12.56=15.44(平方厘米)
答:阴影部分的面积是15.44平方厘米。
【点睛】本题考查圆的面积、梯形的面积公式的灵活运用,根据圆的周长公式求出圆的半径,根据比的应用,求出梯形的下底CB是解题的关键。
16.1.4立方米
【分析】观察图形,圆锥的底面积和圆柱的底面积相等,可设为,利用圆柱的体积公式:V=,h=1.8米,代入表示出圆柱的体积,利用圆锥的体积公式:V=,h=0.9米,代入表示出圆锥的体积,圆柱的体积+圆锥的体积=9.8,求出,再通过圆锥的体积公式求出这个圆锥形沙堆的体积。
【详解】
由可得:
(立方米)
答:圆锥形沙堆的体积是1.4立方米。
【点睛】此题的解理关键是认识到圆柱和圆锥的底面积相等并通过体积公式求出底面积,再根据圆锥的体积公式即可得解。
17.11.25米
【分析】根据长方体体积=底面积×高,可求出长方体铁块的体积,把长方体铁块熔铸成圆锥,体积不变,已知圆锥的底面积,则根据圆锥的高=3×圆锥的体积÷底面积即可得圆锥的高是多少米。
【详解】6分米=0.6米
0.5×0.6=0.3(立方米)
8平方分米=0.08平方米
3×0.3÷0.08
=0.9÷0.08
=11.25(米)
答:圆锥的高是11.25米。
【点睛】本题主要考查了长方体体积公式和圆锥体积公式的灵活应用,注意计算时要先统一单位。
18.(1)20平方厘米
(2)40立方厘米
【分析】(1)占地面积指的是底面积,根据长方形面积=长×宽,列式解答即可。
(2)圆柱露出水面的体积=第一个图长×宽×水深-第二个图长×宽×水深,将圆柱体积看作单位“1”,露出水面的体积÷对应分率=圆柱体积,据此列式解答。
【详解】(1)5×4=20(平方厘米)
答:占地面积是20平方厘米。
(2)12×5×2-5×4×5.5
=120-110
=10(立方厘米)
10÷=40(立方厘米)
答:这个圆柱体铁块的体积是40立方厘米。
【点睛】关键是掌握并灵活运用长方体表面积和体积公式,理解分数除法的意义。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
