小升初应用题专项训练:图形与几何(含答案)-数学六年级下册苏教版
文档属性
| 名称 | 小升初应用题专项训练:图形与几何(含答案)-数学六年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 517.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 17:50:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初应用题专项训练:图形与几何-数学六年级下册苏教版
典型例题解析
1.一块长方形的草坪用1∶2000的比例尺画在纸上,量得这块草坪的图上周长是36厘米,并且长和宽的比是5∶4,这块草坪的实际面积是多少平方米?合多少公顷?
【答案】32000平方米;3.2公顷
【分析】根据实际距离=图上距离÷比例尺,先换算出草坪实际周长,周长÷2=长宽和,将比的前后项看成份数,长宽和÷总份数,求出一份数,一份数分别乘长和宽的对应份数,求出长和宽,根据长方形面积=长×宽,求出草坪的实际面积,根据1公顷=10000平方米,统一单位即可。
【详解】36÷=36×2000=72000(厘米)=720(米)
720÷2÷(5+4)
=360÷9
=40(米)
40×5=200(米)
40×4=160(米)
200×160=32000(平方米)
32000平方米=3.2公顷
答:这块草坪的实际面积是32000平方米,合3.2公顷。
2.李佳学习了圆的面积后,学以致用。自己画了一幅图(如下图),四边形是平行四边形,圆的半径是3厘米。阴影部分面积是多少平方厘米?请你帮李佳算一算。
【答案】9平方厘米
【分析】连接B、D两点,如图所示:
根据圆的特征,①和②部分的面积相等,所以阴影部分相当于三角形ABD的面积,三角形的底是AD,高是DO,根据三角形的面积=底×高÷2,进行解答。
【详解】连接B、D两点,如图所示:
阴影部分的面积=三角形ABD的面积
AD=BC=3×2=6(厘米)
OD=3厘米
6×3÷2=9(平方厘米)
答:阴影部分面积是9平方厘米。
3.把一个高15厘米的圆柱体木料沿着两条互相垂直的直径纵切成完全相同的四块,它的表面积增加了720平方厘米。如果把这个圆柱体削成一个最大的圆锥体,削去了多少立方厘米木料?
【答案】立方厘米
【分析】根据题意,把一个圆柱体木料沿底面直径切成相同的四块,表面积增加720平方厘米,那么增加的表面积是8个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径;用增加的表面积除以8,求出一个切面的面积,再除以高,即可求出圆柱的底面半径;
然后根据圆柱的体积公式V=πr2h,求出这个圆柱体木料的体积;
如果把这个圆柱体削成一个最大的圆锥体,那么这个圆锥和圆柱等底等高,圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,则削去的体积是圆柱体积的(1-),单位“1”已知,用圆柱的体积乘(1-),即可求出削去的体积。
【详解】圆柱的底面半径:
720÷8÷15
=90÷15
=6(厘米)
圆柱的体积:
3.14×62×15
=3.14×36×15
=1695.6(立方厘米)
削去的体积:
1695.6×(1-)
=1695.6×
=1130.4(立方厘米)
答:削去了1130.4立方厘米木料。
【点睛】本题考查圆柱切割的特点,明确圆柱沿底面直径切成四块时,增加的表面积是8个切面的面积,每个切面是以圆柱的底面半径和高为长、宽的长方形,以此为突破口,求出圆柱的底面半径,再利用等底等高时圆锥与圆柱的体积关系解答。
强化训练
1.为了校庆,学校准备编排一套大型集体舞,60名学生围成两个套在一起的大小不同的圆圈,并且每个圆圈上人与人之间的间隔都一样,大圈半径6米,小圈半径4米。那么你知道内、外圈各应站多少名学生吗?
2.一个长方体的棱长和是96分米,相交于一个顶点的三条棱长是连续的自然数。
(1)这个长方体的表面积是多少?
(2)这个长方体的体积是多少?
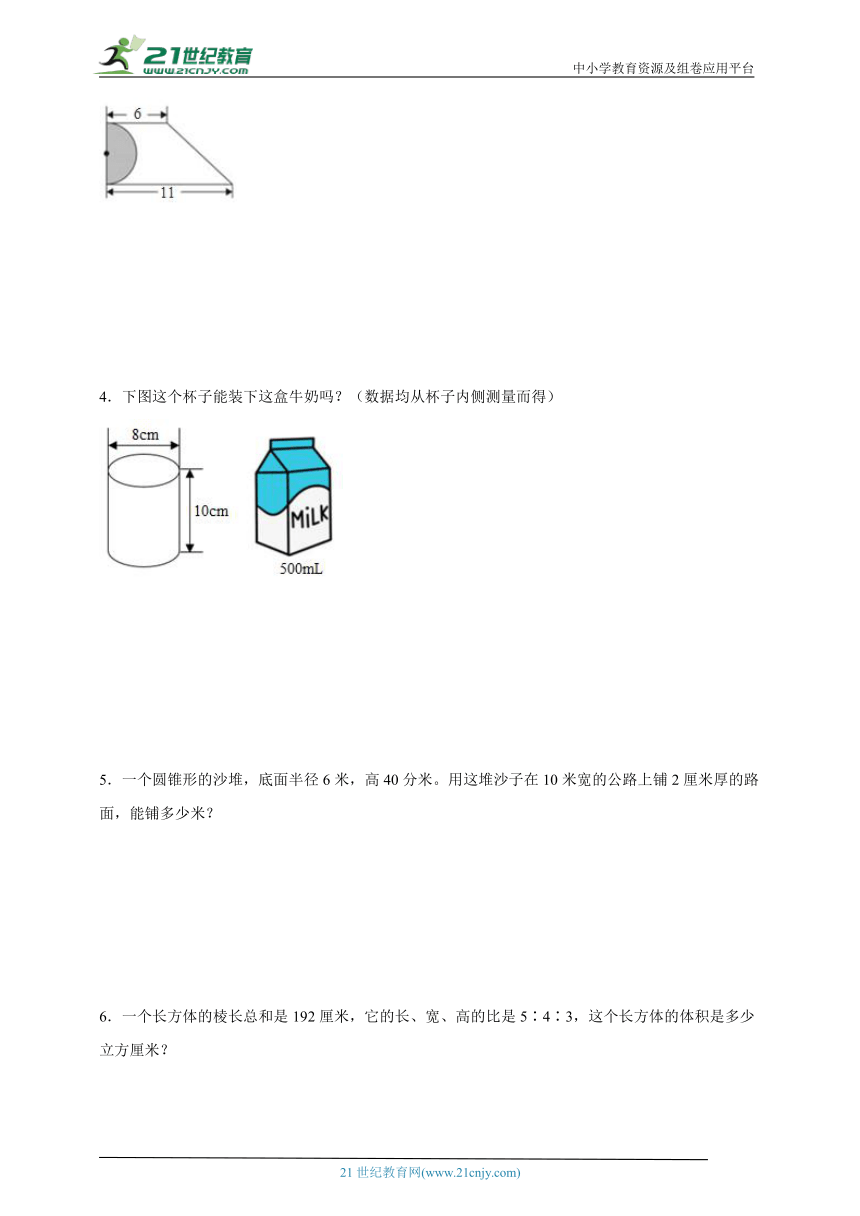
3.已知梯形的面积是51平方厘米,求阴影部分的面积。(单位:厘米)
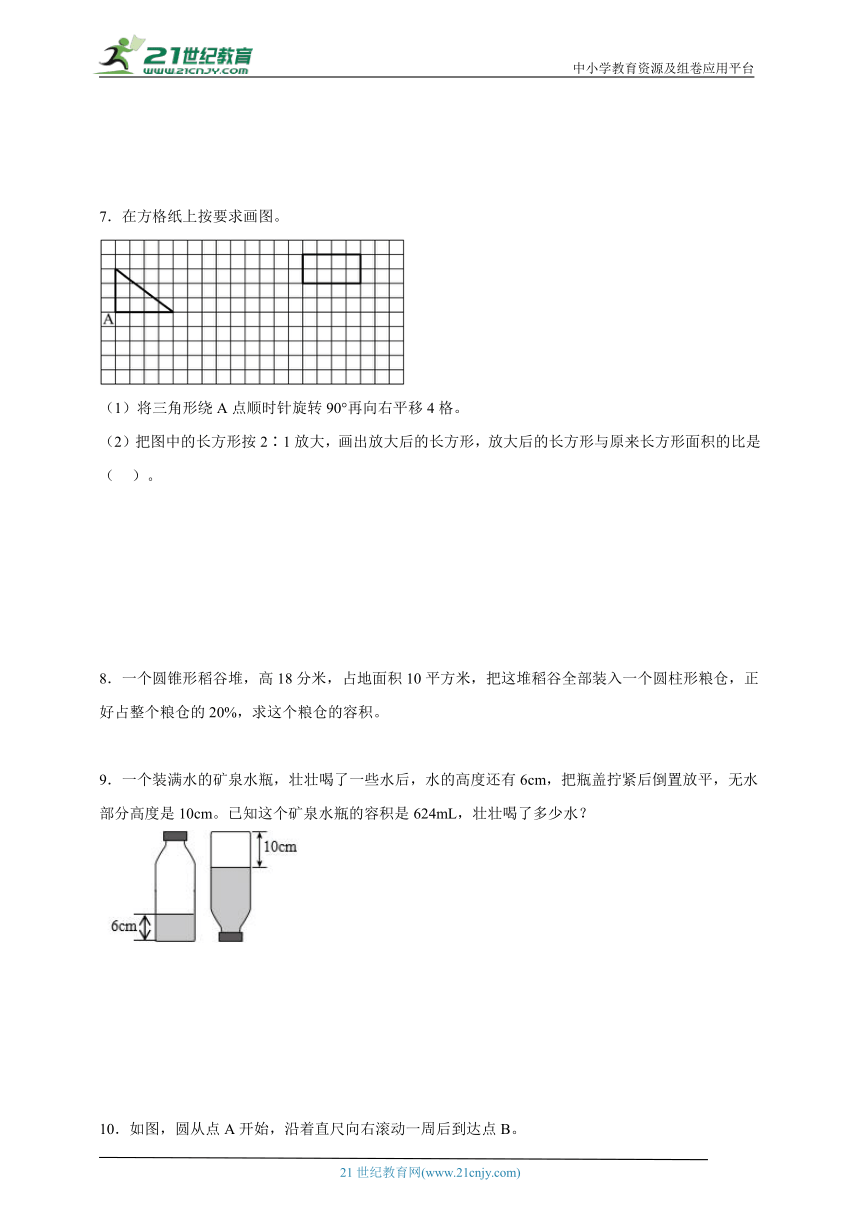
4.下图这个杯子能装下这盒牛奶吗?(数据均从杯子内侧测量而得)
5.一个圆锥形的沙堆,底面半径6米,高40分米。用这堆沙子在10米宽的公路上铺2厘米厚的路面,能铺多少米?
6.一个长方体的棱长总和是192厘米,它的长、宽、高的比是5∶4∶3,这个长方体的体积是多少立方厘米?
7.在方格纸上按要求画图。
(1)将三角形绕A点顺时针旋转90°再向右平移4格。
(2)把图中的长方形按2∶1放大,画出放大后的长方形,放大后的长方形与原来长方形面积的比是( )。
8.一个圆锥形稻谷堆,高18分米,占地面积10平方米,把这堆稻谷全部装入一个圆柱形粮仓,正好占整个粮仓的20%,求这个粮仓的容积。
9.一个装满水的矿泉水瓶,壮壮喝了一些水后,水的高度还有6cm,把瓶盖拧紧后倒置放平,无水部分高度是10cm。已知这个矿泉水瓶的容积是624mL,壮壮喝了多少水?
10.如图,圆从点A开始,沿着直尺向右滚动一周后到达点B。
(1)请在直尺上标出点B的大概位置(在直尺上描上点,并标注上字母B)。
(2)如果这个圆从点A滚动到点C,请计算出滚动后(含起始状态)所覆盖的面积。(取3.14)
11.张医生定做了一个药箱,从侧面看是由一个半圆和一个正方形组成。(如图)
(1)如果忽略厚度不计,这个药箱的容积是多少?
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是多少?
12.如图,三角形ABC是直角三角形,圆的直径是4厘米,阴影甲-阴影乙=2.5平方厘米,则三角形中BC边长是多少厘米?(π取值为3)
13.已知小正方形ABCD的面积是20平方厘米,阴影部分的面积是多少?
14.一个圆柱,在直径位置沿高切开分成完全相同的两部分,两部分的表面积之和比圆柱的表面积增加了40平方分米。这个圆柱的体积是多少?
15.张师傅加工了几种型号的铁皮,如下图,爸爸想买两张来加工一个圆柱形水桶(无盖),假如爸爸请你当参谋:
(1)请从中选择两张铁皮,设计出正好能加工成圆柱形水桶的一种方案,并说明为什么正好能加工成圆柱形水桶。
(2)请根据你选择的方案,求出水桶的容积。
16.如图所示,一个高是1.8分米、底面直径是6厘米的圆柱体塑料水杯,一不小心戳开了一个洞(洞口大小忽略不计),洞口离杯口10厘米。你知道这个水杯最多能装多少毫升的水吗?
参考答案:
1.内圈24名,外圈36名
【分析】根据圆的周长公式C=2πr可知,大小两个圆的周长比等于它们的半径之比,又已知每个圆圈上人与人之间的间隔都一样,那么大小两个圆圈上站的人数之比就等于两个圆的周长之比;根据按比分配的方法,用总人数除以总份数求出一份数,再用一份数分别乘大小圆圈上的人数之比,即可求出内、外圈各应站的人数。
【详解】6∶4=3∶2
60÷(3+2)
=60÷5
=12(名)
内圈站:12×2=24(名)
外圈站:12×3=36(名)
答:内圈应站24名学生,外圈应站36名学生。
【点睛】掌握按比分配的解题方法,明确要分配的总量是多少,以及按照什么比进行分配,求出一份数是解题的关键。
2.(1)382平方分米;(2)504立方分米
【分析】根据长方体的棱长和,可计算出该长方体相交于一个顶点的三条棱的长度和;再根据相交于一个顶点的三条棱长是连续的自然数,即可计算出该长方体的长宽高;再把数值分别代入长方体表面积和体积的计算公式,据此解答。
【详解】(1)96÷4=24(分米)
假设相交于一个顶点的三条棱中其中一条棱长为a,则另外两条棱长分别为(a+1)、(a+2),由a+a+1+a+2=24,解得:a=7,则另外两条棱长分别是8和9。
(7×8+7×9+8×9)×2
=(56+63+72)×2
=191×2
=382(平方分米)
答:这个长方体的表面积是382平方分米。
(2)7×8×9=504(立方分米)
答:这个长方体的体积是504立方分米
【点睛】解答本题的关键是求出该长方体的长宽高,再根据长方体的表面积公式、体积公式进行解答。
3.14.13平方厘米
【分析】通过观察可知,阴影部分的面积是半圆的面积,半圆的直径等于梯形的高,根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(a+b),据此求出梯形的高,再根据半圆的面积是:S=πr2÷2,把数据代入公式解答。
【详解】51×2÷(6+11)
=102÷17
=6(厘米)
3.14×(6÷2)2÷2
=3.14×9÷2
=28.26÷2
=14.13(平方厘米)
答:阴影部分面积是14.13平方厘米
【点睛】本题主要考查梯形的面积公式、圆的面积公式的灵活运用,关键是熟记公式,重点是先求出梯形的高。
4.能
【分析】杯子的底面半径为(8÷2)厘米,高为10厘米,利用圆柱的体积(容积)公式:V=,求出这个杯子的容积,换算单位后,与500毫升比较大小即可得解。
【详解】3.14×(8÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
502.4>500
答:这个杯子能装下这盒牛奶。
【点睛】此题的解题关键是灵活运用圆柱的体积(容积)公式解决问题。
5.753.6米
【分析】先利用圆锥的体积计算公式求出这堆沙堆的体积,再根据沙子的体积不变,代入长方体的体积公式即可求出所铺沙子的长度。
【详解】40分米=4米
2厘米=0.02米
×3.14×62×4÷10÷0.02
=×3.14×36×4÷10÷0.02
=×113.04×4÷10÷0.02
=37.68×4÷10÷0.02
=150.72÷10÷0.02
=15.072÷0.02
=753.6(米)
答:能铺753.6米。
【点睛】此题主要考查圆锥和长方体的体积计算方法,关键是明白:沙子的体积不变。
6.3840立方厘米
【分析】根据长方体的总棱长=(长+宽+高)×4,据此求出一条长、一条宽和一条高的和,然后根据按比分配分别求出长方体的长、宽、高,然后根据长方体的体积=长×宽×高,代入数值进行计算即可。
【详解】192÷4×
=48×
=20(厘米)
192÷4×
=48×
=16(厘米)
192÷4×
=48×
=12(厘米)
20×16×12
=320×12
=3840(立方厘米)
答:这个长方体的体积是3840立方厘米。
【点睛】本题考查长方体的体积,求出长方体的长、宽和高的长度是解题的关键。
7.(1)见详解
(2)图见详解;4∶1
【分析】(1)根据旋转的特征,三角形绕点A顺时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形;再根据平移的特征,把旋转后的三角形的各顶点分别向右平移4格,首尾连接即可得到平移后的图形。
(2)根据图形放大与缩小的意义,把长方形的长、宽分别扩大到原来的2倍,所画出的长方形就是长方形按2∶1放大后的图形,分别求出放大后的长方形的面积、原长方形的面积,根据比的意义写出比并化简。
【详解】(1)作图如下:
(2)如上图:
原长方形的面积=4×2=8
放大后的长方形的面积=8×4=32
所以放大后的长方形与原来长方形面积的比是32∶8=4∶1。
【点睛】此题考查的知识点较多,有作旋转一定度数后的图形;图形的放大与缩小;长方形面积的计算、比的意义等,要求学生熟练掌握。
8.30立方米
【分析】先利用圆锥的体积V=Sh,求出这些谷子的体积,进而利用已知一个数的几百分之几是多少,求这个数,用除法计算的方法,即可求出这个粮仓的容积。
【详解】18分米=1.8米
×10×1.8÷20%
=6÷20%
=30(立方米)
答:这个粮仓的容积是30立方米。
【点睛】此题主要考查圆锥的体积的计算方法在实际中的应用。
9.390毫升
【分析】矿泉水瓶上方是不规则的,将瓶子一正一反放置,可知剩余的水是高6厘米的圆柱,喝掉的水(空着的部分)是高10厘米的圆柱,则满瓶时水的总高度是16厘米,根据圆柱的体积÷高=底面积,求出底面积,再乘10即可。
【详解】624÷(6+10)×10
=624÷16×10
=390(立方厘米)
=390(毫升)
答:壮壮喝了390毫升的水。
【点睛】根据瓶子内水的体积和空气的体积不变,将不规则的瓶子转化成规则的圆柱解题是此题的关键。
10.(1)见详解
(2)21.14平方厘米
【分析】(1)通过观察图形,这个圆的直径是2厘米,根据圆的周长公式:,把数据代入公式求出这个圆的周长,据此在图中标出B点位置即可。
(2)根据题意可知,如果这个圆从点A滚动到点C,圆在整个滚动过程中所覆盖的面积=长为14-5=9(厘米)、宽为6-4=2(厘米)的长方形面积+一个圆的面积,然后再根据长方形的面积公式S=ab,圆的面积公式,把数据代入公式解答。
【详解】(1)3.14×(6-4)
=3.14×2
=6.28(厘米)
6.28+5=11.28(厘米)
作图如下:
(2)(14-5)×(6-4)+3.14×[(6-4)÷2]2
=9×2+3.14×[2÷2]2
=18+3.14×1
=18+3.14
=21.14(平方厘米)
答:所覆盖的面积是21.14平方厘米。
【点睛】此题主要考查圆的周长公式、面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
11.(1)27.85立方分米
(2)46.84平方分米
【分析】(1)这个药箱的容积包括一个长方体的容积和半个圆柱的体积,利用长方体的体积公式:体积=长×宽×高;圆柱的体积公式:体积=底面积×高;代入数据求出长方体的体积和半个圆柱的体积,再相加,即可解答。
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是指4个长方体的面和圆柱的一个底面积和圆柱侧面积的一半,根据长方形面积公式:长×宽;圆柱的表面积公式:底面面积+侧面积÷2,代入数据,求出面积,再相加,即可解答。
【详解】(1)5×2×2+3.14×(2÷2)2×5÷2
=10×2+3.14×1×5÷2
=20+3.14×5÷2
=20+15.7÷2
=20+7.85
=27.85(立方分米)
答:这个药箱的容积是27.85立方分米。
(2)2×2×2+2×5×2+3.14×2×5÷2+3.14×(2÷2)2
=4×2+10×2+6.28×5÷2+3.14×1
=8+20+31.4÷2+3.14
=8+20+15.7+3.14
=28+15.7+3.14
=43.7+3.14
=46.84(平方分米)
答:刷漆的面积是46.84平方分米。
【点睛】本题考查了长方体和圆柱体积公式及表面积公式的应用;关键是熟记公式。
12.4.75厘米
【分析】阴影甲的面积=半圆的面积-空白部分的面积,阴影乙的面积=三角形ABC的面积-空白部分的面积,再根据阴影甲-阴影乙=2.5平方厘米,所以半圆的面积-空白部分的面积-(三角形ABC的面积-空白部分的面积)=2.5平方厘米,即半圆的面积-三角形ABC的面积=2.5平方厘米,利用圆和三角形的面积公式,代入数据求解即可。
【详解】3×(4÷2)2-4×BC÷2=2.5
3×4-2BC=2.5
12-2BC=2.5
2BC=12-2.5
2BC=9.5
BC=4.75
答:三角形中BC边长是4.75厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
13.8.6平方厘米
【分析】设圆的半径是r厘米,小正方形ABCD的面积是由4个底边长和高都为r的直角三角形组成,即r×r÷2×4=20,求出圆的半径的平方;大正方形的边长是2r厘米,求出大正方形的面积,再根据阴影部分的面积=大正方形面积-圆的面积,利用圆的面积和正方形的面积公式求解即可。
【详解】解:设圆的半径是r厘米,则大正方形的边长是2r厘米。
r×r÷2×4=20
r2×2=20
r2=20÷2
r2=10
2r×2r=4r2=4×10=40(平方厘米)
40-3.14×r2
=40-3.14×10
=40-31.4
=8.6(平方厘米)
答:阴影部分的面积是8.6平方厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
14.62.8立方分米
【分析】通过观察图形可知,把圆柱纵切成两半,表面积增加的是两个截面的面积,每个截面的长等于圆柱的高,每个截面的宽等于圆柱的底面直径,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【详解】40÷2÷5
=20÷5
=4(分米)
3.14×(4÷2)2×5
=3.14×4×5
=12.56×5
=62.8(立方分米)
答:这个圆柱的体积是62.8立方分米。
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆柱的底面直径。
15.(1)见详解;(2)62.8立方分米(答案不唯一)
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=,把数据代入公式求出两个圆的周长,然后与两个长方形的长进行比较,即可确定哪两个图形可以搭配使用。
(2)先确定方案,再根据圆柱的容积(体积)公式:V=,把数据代入公式解答。
【详解】(1)2×3.14×3=18.84(分米)
2×3.14×2=12.56(分米)
因此可知,①和④搭配,②和③搭配。
答:能加工成圆柱形水桶的方案有两种,分别是①和④搭配,②和③搭配,因为①的周长等于④的长,②的周长等于③的长。
(2)我选择②和③搭配。
3.14×22×5
=3.14×4×5
=62.8(立方分米)
答:水桶的容积是62.8立方分米。
【点睛】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆柱的容积(体积)公式及应用,关键是熟记公式。
16.226.08毫升
【分析】根据题意,1.8分米=18厘米,瓶内装水的高度最多为18-10=8(厘米),利用圆柱的体积公式解答,求出水的体积即可。
【详解】1.8分米=18厘米
3.14×(6÷2)2×(18-10)
=3.14×9×8
=226.08(立方厘米)
226.08立方厘米=226.08毫升
答:这个水杯最多能装226.08毫升的水。
【点睛】解答此题的关键是根据瓶高和洞口离杯口的高度求出装水的高度。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初应用题专项训练:图形与几何-数学六年级下册苏教版
典型例题解析
1.一块长方形的草坪用1∶2000的比例尺画在纸上,量得这块草坪的图上周长是36厘米,并且长和宽的比是5∶4,这块草坪的实际面积是多少平方米?合多少公顷?
【答案】32000平方米;3.2公顷
【分析】根据实际距离=图上距离÷比例尺,先换算出草坪实际周长,周长÷2=长宽和,将比的前后项看成份数,长宽和÷总份数,求出一份数,一份数分别乘长和宽的对应份数,求出长和宽,根据长方形面积=长×宽,求出草坪的实际面积,根据1公顷=10000平方米,统一单位即可。
【详解】36÷=36×2000=72000(厘米)=720(米)
720÷2÷(5+4)
=360÷9
=40(米)
40×5=200(米)
40×4=160(米)
200×160=32000(平方米)
32000平方米=3.2公顷
答:这块草坪的实际面积是32000平方米,合3.2公顷。
2.李佳学习了圆的面积后,学以致用。自己画了一幅图(如下图),四边形是平行四边形,圆的半径是3厘米。阴影部分面积是多少平方厘米?请你帮李佳算一算。
【答案】9平方厘米
【分析】连接B、D两点,如图所示:
根据圆的特征,①和②部分的面积相等,所以阴影部分相当于三角形ABD的面积,三角形的底是AD,高是DO,根据三角形的面积=底×高÷2,进行解答。
【详解】连接B、D两点,如图所示:
阴影部分的面积=三角形ABD的面积
AD=BC=3×2=6(厘米)
OD=3厘米
6×3÷2=9(平方厘米)
答:阴影部分面积是9平方厘米。
3.把一个高15厘米的圆柱体木料沿着两条互相垂直的直径纵切成完全相同的四块,它的表面积增加了720平方厘米。如果把这个圆柱体削成一个最大的圆锥体,削去了多少立方厘米木料?
【答案】立方厘米
【分析】根据题意,把一个圆柱体木料沿底面直径切成相同的四块,表面积增加720平方厘米,那么增加的表面积是8个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径;用增加的表面积除以8,求出一个切面的面积,再除以高,即可求出圆柱的底面半径;
然后根据圆柱的体积公式V=πr2h,求出这个圆柱体木料的体积;
如果把这个圆柱体削成一个最大的圆锥体,那么这个圆锥和圆柱等底等高,圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,则削去的体积是圆柱体积的(1-),单位“1”已知,用圆柱的体积乘(1-),即可求出削去的体积。
【详解】圆柱的底面半径:
720÷8÷15
=90÷15
=6(厘米)
圆柱的体积:
3.14×62×15
=3.14×36×15
=1695.6(立方厘米)
削去的体积:
1695.6×(1-)
=1695.6×
=1130.4(立方厘米)
答:削去了1130.4立方厘米木料。
【点睛】本题考查圆柱切割的特点,明确圆柱沿底面直径切成四块时,增加的表面积是8个切面的面积,每个切面是以圆柱的底面半径和高为长、宽的长方形,以此为突破口,求出圆柱的底面半径,再利用等底等高时圆锥与圆柱的体积关系解答。
强化训练
1.为了校庆,学校准备编排一套大型集体舞,60名学生围成两个套在一起的大小不同的圆圈,并且每个圆圈上人与人之间的间隔都一样,大圈半径6米,小圈半径4米。那么你知道内、外圈各应站多少名学生吗?
2.一个长方体的棱长和是96分米,相交于一个顶点的三条棱长是连续的自然数。
(1)这个长方体的表面积是多少?
(2)这个长方体的体积是多少?
3.已知梯形的面积是51平方厘米,求阴影部分的面积。(单位:厘米)
4.下图这个杯子能装下这盒牛奶吗?(数据均从杯子内侧测量而得)
5.一个圆锥形的沙堆,底面半径6米,高40分米。用这堆沙子在10米宽的公路上铺2厘米厚的路面,能铺多少米?
6.一个长方体的棱长总和是192厘米,它的长、宽、高的比是5∶4∶3,这个长方体的体积是多少立方厘米?
7.在方格纸上按要求画图。
(1)将三角形绕A点顺时针旋转90°再向右平移4格。
(2)把图中的长方形按2∶1放大,画出放大后的长方形,放大后的长方形与原来长方形面积的比是( )。
8.一个圆锥形稻谷堆,高18分米,占地面积10平方米,把这堆稻谷全部装入一个圆柱形粮仓,正好占整个粮仓的20%,求这个粮仓的容积。
9.一个装满水的矿泉水瓶,壮壮喝了一些水后,水的高度还有6cm,把瓶盖拧紧后倒置放平,无水部分高度是10cm。已知这个矿泉水瓶的容积是624mL,壮壮喝了多少水?
10.如图,圆从点A开始,沿着直尺向右滚动一周后到达点B。
(1)请在直尺上标出点B的大概位置(在直尺上描上点,并标注上字母B)。
(2)如果这个圆从点A滚动到点C,请计算出滚动后(含起始状态)所覆盖的面积。(取3.14)
11.张医生定做了一个药箱,从侧面看是由一个半圆和一个正方形组成。(如图)
(1)如果忽略厚度不计,这个药箱的容积是多少?
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是多少?
12.如图,三角形ABC是直角三角形,圆的直径是4厘米,阴影甲-阴影乙=2.5平方厘米,则三角形中BC边长是多少厘米?(π取值为3)
13.已知小正方形ABCD的面积是20平方厘米,阴影部分的面积是多少?
14.一个圆柱,在直径位置沿高切开分成完全相同的两部分,两部分的表面积之和比圆柱的表面积增加了40平方分米。这个圆柱的体积是多少?
15.张师傅加工了几种型号的铁皮,如下图,爸爸想买两张来加工一个圆柱形水桶(无盖),假如爸爸请你当参谋:
(1)请从中选择两张铁皮,设计出正好能加工成圆柱形水桶的一种方案,并说明为什么正好能加工成圆柱形水桶。
(2)请根据你选择的方案,求出水桶的容积。
16.如图所示,一个高是1.8分米、底面直径是6厘米的圆柱体塑料水杯,一不小心戳开了一个洞(洞口大小忽略不计),洞口离杯口10厘米。你知道这个水杯最多能装多少毫升的水吗?
参考答案:
1.内圈24名,外圈36名
【分析】根据圆的周长公式C=2πr可知,大小两个圆的周长比等于它们的半径之比,又已知每个圆圈上人与人之间的间隔都一样,那么大小两个圆圈上站的人数之比就等于两个圆的周长之比;根据按比分配的方法,用总人数除以总份数求出一份数,再用一份数分别乘大小圆圈上的人数之比,即可求出内、外圈各应站的人数。
【详解】6∶4=3∶2
60÷(3+2)
=60÷5
=12(名)
内圈站:12×2=24(名)
外圈站:12×3=36(名)
答:内圈应站24名学生,外圈应站36名学生。
【点睛】掌握按比分配的解题方法,明确要分配的总量是多少,以及按照什么比进行分配,求出一份数是解题的关键。
2.(1)382平方分米;(2)504立方分米
【分析】根据长方体的棱长和,可计算出该长方体相交于一个顶点的三条棱的长度和;再根据相交于一个顶点的三条棱长是连续的自然数,即可计算出该长方体的长宽高;再把数值分别代入长方体表面积和体积的计算公式,据此解答。
【详解】(1)96÷4=24(分米)
假设相交于一个顶点的三条棱中其中一条棱长为a,则另外两条棱长分别为(a+1)、(a+2),由a+a+1+a+2=24,解得:a=7,则另外两条棱长分别是8和9。
(7×8+7×9+8×9)×2
=(56+63+72)×2
=191×2
=382(平方分米)
答:这个长方体的表面积是382平方分米。
(2)7×8×9=504(立方分米)
答:这个长方体的体积是504立方分米
【点睛】解答本题的关键是求出该长方体的长宽高,再根据长方体的表面积公式、体积公式进行解答。
3.14.13平方厘米
【分析】通过观察可知,阴影部分的面积是半圆的面积,半圆的直径等于梯形的高,根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(a+b),据此求出梯形的高,再根据半圆的面积是:S=πr2÷2,把数据代入公式解答。
【详解】51×2÷(6+11)
=102÷17
=6(厘米)
3.14×(6÷2)2÷2
=3.14×9÷2
=28.26÷2
=14.13(平方厘米)
答:阴影部分面积是14.13平方厘米
【点睛】本题主要考查梯形的面积公式、圆的面积公式的灵活运用,关键是熟记公式,重点是先求出梯形的高。
4.能
【分析】杯子的底面半径为(8÷2)厘米,高为10厘米,利用圆柱的体积(容积)公式:V=,求出这个杯子的容积,换算单位后,与500毫升比较大小即可得解。
【详解】3.14×(8÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
502.4>500
答:这个杯子能装下这盒牛奶。
【点睛】此题的解题关键是灵活运用圆柱的体积(容积)公式解决问题。
5.753.6米
【分析】先利用圆锥的体积计算公式求出这堆沙堆的体积,再根据沙子的体积不变,代入长方体的体积公式即可求出所铺沙子的长度。
【详解】40分米=4米
2厘米=0.02米
×3.14×62×4÷10÷0.02
=×3.14×36×4÷10÷0.02
=×113.04×4÷10÷0.02
=37.68×4÷10÷0.02
=150.72÷10÷0.02
=15.072÷0.02
=753.6(米)
答:能铺753.6米。
【点睛】此题主要考查圆锥和长方体的体积计算方法,关键是明白:沙子的体积不变。
6.3840立方厘米
【分析】根据长方体的总棱长=(长+宽+高)×4,据此求出一条长、一条宽和一条高的和,然后根据按比分配分别求出长方体的长、宽、高,然后根据长方体的体积=长×宽×高,代入数值进行计算即可。
【详解】192÷4×
=48×
=20(厘米)
192÷4×
=48×
=16(厘米)
192÷4×
=48×
=12(厘米)
20×16×12
=320×12
=3840(立方厘米)
答:这个长方体的体积是3840立方厘米。
【点睛】本题考查长方体的体积,求出长方体的长、宽和高的长度是解题的关键。
7.(1)见详解
(2)图见详解;4∶1
【分析】(1)根据旋转的特征,三角形绕点A顺时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形;再根据平移的特征,把旋转后的三角形的各顶点分别向右平移4格,首尾连接即可得到平移后的图形。
(2)根据图形放大与缩小的意义,把长方形的长、宽分别扩大到原来的2倍,所画出的长方形就是长方形按2∶1放大后的图形,分别求出放大后的长方形的面积、原长方形的面积,根据比的意义写出比并化简。
【详解】(1)作图如下:
(2)如上图:
原长方形的面积=4×2=8
放大后的长方形的面积=8×4=32
所以放大后的长方形与原来长方形面积的比是32∶8=4∶1。
【点睛】此题考查的知识点较多,有作旋转一定度数后的图形;图形的放大与缩小;长方形面积的计算、比的意义等,要求学生熟练掌握。
8.30立方米
【分析】先利用圆锥的体积V=Sh,求出这些谷子的体积,进而利用已知一个数的几百分之几是多少,求这个数,用除法计算的方法,即可求出这个粮仓的容积。
【详解】18分米=1.8米
×10×1.8÷20%
=6÷20%
=30(立方米)
答:这个粮仓的容积是30立方米。
【点睛】此题主要考查圆锥的体积的计算方法在实际中的应用。
9.390毫升
【分析】矿泉水瓶上方是不规则的,将瓶子一正一反放置,可知剩余的水是高6厘米的圆柱,喝掉的水(空着的部分)是高10厘米的圆柱,则满瓶时水的总高度是16厘米,根据圆柱的体积÷高=底面积,求出底面积,再乘10即可。
【详解】624÷(6+10)×10
=624÷16×10
=390(立方厘米)
=390(毫升)
答:壮壮喝了390毫升的水。
【点睛】根据瓶子内水的体积和空气的体积不变,将不规则的瓶子转化成规则的圆柱解题是此题的关键。
10.(1)见详解
(2)21.14平方厘米
【分析】(1)通过观察图形,这个圆的直径是2厘米,根据圆的周长公式:,把数据代入公式求出这个圆的周长,据此在图中标出B点位置即可。
(2)根据题意可知,如果这个圆从点A滚动到点C,圆在整个滚动过程中所覆盖的面积=长为14-5=9(厘米)、宽为6-4=2(厘米)的长方形面积+一个圆的面积,然后再根据长方形的面积公式S=ab,圆的面积公式,把数据代入公式解答。
【详解】(1)3.14×(6-4)
=3.14×2
=6.28(厘米)
6.28+5=11.28(厘米)
作图如下:
(2)(14-5)×(6-4)+3.14×[(6-4)÷2]2
=9×2+3.14×[2÷2]2
=18+3.14×1
=18+3.14
=21.14(平方厘米)
答:所覆盖的面积是21.14平方厘米。
【点睛】此题主要考查圆的周长公式、面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
11.(1)27.85立方分米
(2)46.84平方分米
【分析】(1)这个药箱的容积包括一个长方体的容积和半个圆柱的体积,利用长方体的体积公式:体积=长×宽×高;圆柱的体积公式:体积=底面积×高;代入数据求出长方体的体积和半个圆柱的体积,再相加,即可解答。
(2)如果给药箱外表面刷漆(底面不刷),刷漆的面积是指4个长方体的面和圆柱的一个底面积和圆柱侧面积的一半,根据长方形面积公式:长×宽;圆柱的表面积公式:底面面积+侧面积÷2,代入数据,求出面积,再相加,即可解答。
【详解】(1)5×2×2+3.14×(2÷2)2×5÷2
=10×2+3.14×1×5÷2
=20+3.14×5÷2
=20+15.7÷2
=20+7.85
=27.85(立方分米)
答:这个药箱的容积是27.85立方分米。
(2)2×2×2+2×5×2+3.14×2×5÷2+3.14×(2÷2)2
=4×2+10×2+6.28×5÷2+3.14×1
=8+20+31.4÷2+3.14
=8+20+15.7+3.14
=28+15.7+3.14
=43.7+3.14
=46.84(平方分米)
答:刷漆的面积是46.84平方分米。
【点睛】本题考查了长方体和圆柱体积公式及表面积公式的应用;关键是熟记公式。
12.4.75厘米
【分析】阴影甲的面积=半圆的面积-空白部分的面积,阴影乙的面积=三角形ABC的面积-空白部分的面积,再根据阴影甲-阴影乙=2.5平方厘米,所以半圆的面积-空白部分的面积-(三角形ABC的面积-空白部分的面积)=2.5平方厘米,即半圆的面积-三角形ABC的面积=2.5平方厘米,利用圆和三角形的面积公式,代入数据求解即可。
【详解】3×(4÷2)2-4×BC÷2=2.5
3×4-2BC=2.5
12-2BC=2.5
2BC=12-2.5
2BC=9.5
BC=4.75
答:三角形中BC边长是4.75厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
13.8.6平方厘米
【分析】设圆的半径是r厘米,小正方形ABCD的面积是由4个底边长和高都为r的直角三角形组成,即r×r÷2×4=20,求出圆的半径的平方;大正方形的边长是2r厘米,求出大正方形的面积,再根据阴影部分的面积=大正方形面积-圆的面积,利用圆的面积和正方形的面积公式求解即可。
【详解】解:设圆的半径是r厘米,则大正方形的边长是2r厘米。
r×r÷2×4=20
r2×2=20
r2=20÷2
r2=10
2r×2r=4r2=4×10=40(平方厘米)
40-3.14×r2
=40-3.14×10
=40-31.4
=8.6(平方厘米)
答:阴影部分的面积是8.6平方厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
14.62.8立方分米
【分析】通过观察图形可知,把圆柱纵切成两半,表面积增加的是两个截面的面积,每个截面的长等于圆柱的高,每个截面的宽等于圆柱的底面直径,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【详解】40÷2÷5
=20÷5
=4(分米)
3.14×(4÷2)2×5
=3.14×4×5
=12.56×5
=62.8(立方分米)
答:这个圆柱的体积是62.8立方分米。
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆柱的底面直径。
15.(1)见详解;(2)62.8立方分米(答案不唯一)
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=,把数据代入公式求出两个圆的周长,然后与两个长方形的长进行比较,即可确定哪两个图形可以搭配使用。
(2)先确定方案,再根据圆柱的容积(体积)公式:V=,把数据代入公式解答。
【详解】(1)2×3.14×3=18.84(分米)
2×3.14×2=12.56(分米)
因此可知,①和④搭配,②和③搭配。
答:能加工成圆柱形水桶的方案有两种,分别是①和④搭配,②和③搭配,因为①的周长等于④的长,②的周长等于③的长。
(2)我选择②和③搭配。
3.14×22×5
=3.14×4×5
=62.8(立方分米)
答:水桶的容积是62.8立方分米。
【点睛】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆柱的容积(体积)公式及应用,关键是熟记公式。
16.226.08毫升
【分析】根据题意,1.8分米=18厘米,瓶内装水的高度最多为18-10=8(厘米),利用圆柱的体积公式解答,求出水的体积即可。
【详解】1.8分米=18厘米
3.14×(6÷2)2×(18-10)
=3.14×9×8
=226.08(立方厘米)
226.08立方厘米=226.08毫升
答:这个水杯最多能装226.08毫升的水。
【点睛】解答此题的关键是根据瓶高和洞口离杯口的高度求出装水的高度。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
