小升初高频考点检测卷(含答案)-数学六年级下册青岛版
文档属性
| 名称 | 小升初高频考点检测卷(含答案)-数学六年级下册青岛版 |  | |
| 格式 | docx | ||
| 文件大小 | 723.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 18:38:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初高频考点检测卷-数学六年级下册青岛版
一、选择题
1.下面四个图形中,经过折叠能围成下边正方体纸盒的是( )。
A. B.
C. D.
2.下面的式子中,是方程的是( )。
A.3x+5 B.3y-7<8 C. D.81÷9=9
3.一件商品,提高原价的20%,现在又降价20%,商品现在的价格( )。
A.高于原价 B.等于原价 C.低于原价 D.无法确定
4.下列说法正确的是( )。
A.一个数(0除外)除以假分数,商一定小于被除数
B.把25克盐放入100克水中,盐占盐水质量的20%
C.一根木头锯成3段需要6分,那么锯成6段需要12分
D.甲数比乙数多,乙数就比甲数少
5.有甲、乙两筐苹果,如果从甲筐苹果里取出放入乙筐后,两筐苹果的质量相等,那么原来甲、乙两筐苹果的质量比是( )。
A.4∶3 B.7∶5 C.7∶6 D.3∶4
6.一个长方体的长、宽、高分别为a米、b米、h米,如果高增加2米,新的长方体体积比原来增加( )立方米。
A.2ab B.2abh C.ab(h+2) D.abh+22
二、填空题
7.如果把平均成绩记为0分,﹢9分表示比平均成绩( ),﹣7分表示比平均成绩( ),比平均成绩低3分记作( )分。
8.( )∶12==0.25=( )折=( )(填成数)。
9.有一串彩灯是按2红、3绿、5黄的顺序依次排列的。第27盏彩灯是( )色,前60盏中,有( )盏绿灯。
10.用药店的会员卡买药可打九五折,奶奶用会员卡买了一瓶药,省了3.6元,这瓶药原价( )元。
11.一个圆柱的底面直径是8cm,高为1dm,这个圆柱表面积是( )cm2,体积是( )cm3。
12.商店运来苹果吨,运来梨的吨数是苹果的,运来梨( )吨,运来的苹果和梨一共( )吨。
三、判断题
13.一根木棒截成7段要9分钟,那么把这根木棒截成两段,需要1.5分钟。( )
14.如果小刚站在小明北偏东45°方向处,那么小明就在小刚西偏南45°的方向处。( )
15.同一平面内的两条直线相交,只有一个交点。( )
16.把一个圆柱形橡皮泥揉成与它等底的圆锥,高将扩大到原来的3倍。( )
17.2a+5错写成2(a+5),结果比原来多5。( )
18.从下面的盒子里任意摸出一个球,摸到的黄球的可能性最大。( )
四、计算题
19.直接写得数。
20.用你喜欢的方法计算,看谁算得又对又快。
21.解方程(或比例)。
(+)=35%
22.求图中阴影部分的面积。(单位:厘米)(取)
五、解答题
23.甲、乙两车分别从A、B两地同时出发相对开出,4小时相遇,相遇后两车都以各自原速继续行驶,已知甲车又行驶了5小时到达B地,乙车又行多少时间到达A地?
24.师徒两人同时加工440个零件,已知师傅每小时加工70个,徒弟与师傅的工作效率比是。师徒两人几小时后完成加工任务?
25.某小学原来平均每天产生垃圾30千克,自从开展分类投放垃圾后,现在平均每天少产生的垃圾,现在平均每天产生垃圾多少千克?
26. 2023年6月5日是第50个“世界环境日”,六1班同学开展“爱护环境,从我做起”主题活动。活动中收集到塑料瓶150个,收集的易拉罐个数是塑料瓶的,六班同学收集易拉罐和塑料瓶共多少个?
27.把一个圆柱形木块按两种方式锯开。如果沿底面直径纵向锯成4块(下图左),表面积会增加192平方厘米;如果横向锯两次形成3个小圆柱(下图右),表面积会增加50.24平方厘米,原来这个圆柱形木块的体积是多少立方厘米呢?
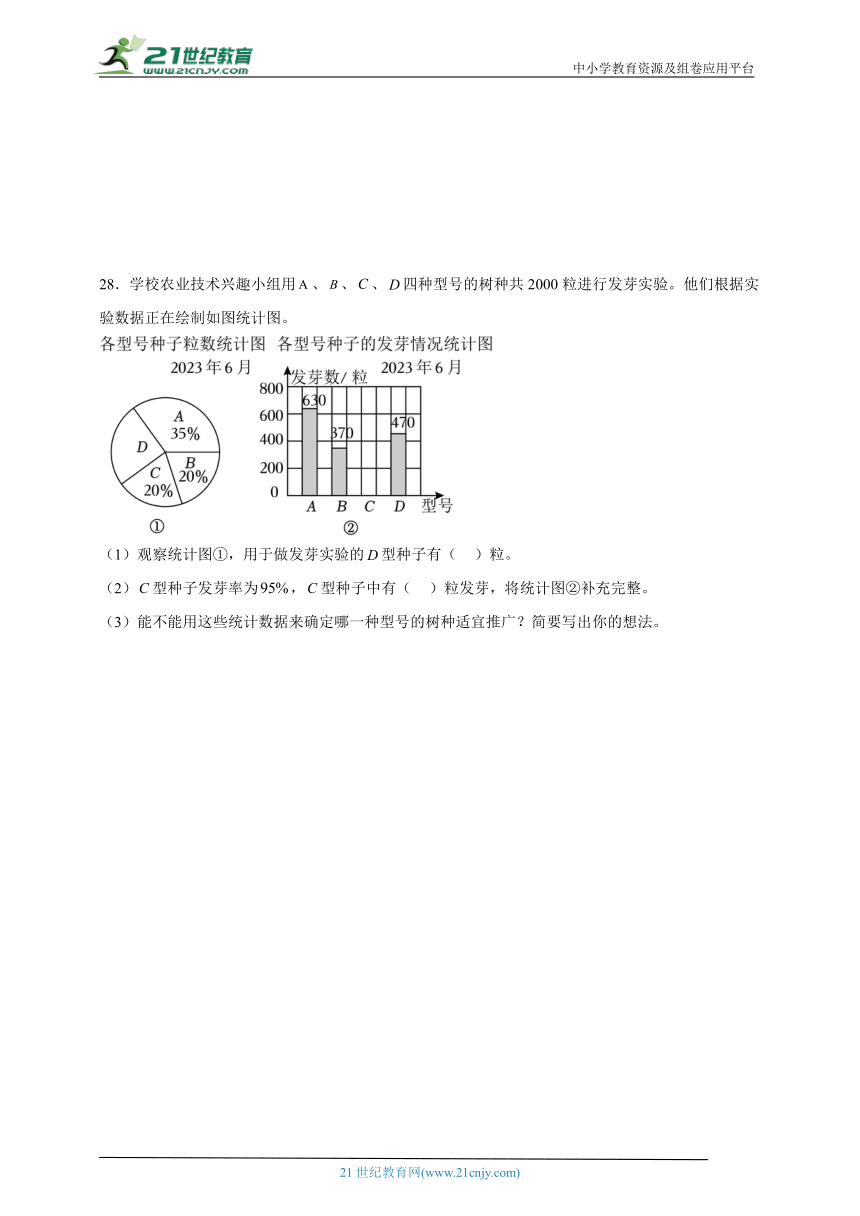
28.学校农业技术兴趣小组用、、、四种型号的树种共2000粒进行发芽实验。他们根据实验数据正在绘制如图统计图。
(1)观察统计图①,用于做发芽实验的型种子有( )粒。
(2)型种子发芽率为,型种子中有( )粒发芽,将统计图②补充完整。
(3)能不能用这些统计数据来确定哪一种型号的树种适宜推广?简要写出你的想法。
参考答案:
1.B
【分析】
从正方体的纸盒上面的图形可以看成,三个图形不应该是对面。且三角形的一个角对着圆形,据此解答即可。
【详解】
A.三角形和正方形成了对面
B.正好是这三个面
C.三角形和正方形成了对面
D.三角形和圆形成了对面
故答案为:B
2.C
【分析】
含有未知数的等式叫做方程;据此解答。
【详解】A.3x+5,含有未知数,但不是等式,不是方程;
B.3y-7<8,含有未知数,但不是等式,不是方程;
C.,含有未知数,是等式,是方程;
D.81÷9=9,是等式,但不含有未知数,不是方程;
故答案为:C
3.C
【分析】一种商品提价20%,是在原来的价格上提的20%,把原来的价格看作单位“1”,那么提价后的价格是(l+20%),又降价20%,是在提价的基础上降低了20%,此时的单位“1”是提价后的价格,据此求出现价与原价比较即可。
【详解】由分析可知,现价是:
(1+20%)×(1-20%)
=1.2×0.8
=0.96
=96%
商品现在的价格低于原价。
故答案为:C
4.B
【分析】当被除数不等于0时;要弄清楚假分数的数值,分为等于1(分子等于分母)与大于1(分子大于分母)两种情况,进行分类讨论得出答案;
把25克盐放入100克水中,则盐水为25+100克,根据分数的意义,盐占盐水的25÷(100+25);
每次把一根木头可以锯成两段,锯成三段需要锯2次,用6分钟除以2,求出每次需要的时间;锯成6段需要锯5次,用每次需要的时间乘5即可求解;
根据“甲数比乙数多”知道是把乙数看作单位“1”,即甲数(1+),然后用两数的差除以甲数,即可得出乙数比甲数少几分之几,然后比较即可判断。
【详解】A.被除数不是0时;当假分数的数值等于1时,一个数(0除外)除以假分数,所得的商等于这个数;当假分数的数值大于1时,一个数(0除外)除以假分数(乘以真分数),所得的商小于这个数;所以一个数除以假分数,商可能小于被除数,也可能等于被除数;原题说法错误;
B.25÷(100+25)×100%
=25÷125×100%
=0.2×100%
=20%,盐占盐水的20%;原题说法正确;
C.6÷(3-1)×(6-1)
=6÷2×5
=3×5
=15(分钟)把它锯成6段需要15分钟,原题说法错误;
D.÷(1+)
=÷
=×
=,原题说法错误;
故答案为:B
5.B
【分析】根据分数的意义,甲筐苹果平均分成7份,取出1份后甲筐中则有份,乙筐得到1份后和甲筐同样多,也是6份,那么乙筐中原有份,从而求得。
【详解】根据分析可知:
原来甲、乙两筐苹果的质量比是7∶5
故答案为:B
6.A
【分析】
根据题意可知,长、宽不变,高增加2米,所以增加的体积是长为a米、宽为b米、高为2米的长方体,根据长方体的体积=长×宽×高,用a×b×2即可求出增加的体积。
【详解】a×b×2=2ab(立方米)
新的长方体体积比原来增加2ab立方米。
故答案为:A
7. 高9分 低7分 ﹣3
【分析】正负数可以表示相反意义的量,以平均成绩为标准,高于平均成绩记为正,低于平均成绩记为负,据此分析。
【详解】如果把平均成绩记为0分,﹢9分表示比平均成绩高9分,﹣7分表示比平均成绩低7分,比平均成绩低3分记作﹣3分。
8.3;5;二五;二成五
【分析】分数的分子相当于比的前项,分母相当于比的后项,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此先将小数化成分数,根据分数与比的关系,以及它们通用的基本性质进行填空,小数化百分数,小数点向右移动两位,添上百分号即可,根据几折就是百分之几十,几成就是百分之几十,确定折数和成数。
【详解】0.25=,12÷4×1=3;20÷4×1=5;0.25=25%=二五折=二成五
3∶12==0.25=二五折=二成五
9. 黄 18
【分析】这串彩灯按照颜色特点排列的规律是:10盏灯一个循环周期,分别按照:2红、3绿、5黄的顺序依次循环排列;用27除以10所得商为循环了几个周期,余数则为这几盏灯;用60除以10所得商为循环了几个周期,每一个循环周期中有3盏绿灯,用3乘循环的周期,所得结果即为绿灯的数量。
【详解】2+3+5=10(盏)
27÷10=2(个)……7(盏)
第7盏灯是黄色。
60÷10×3
=6×3
=18(盏)
因此第27盏彩灯是黄色,前60盏中,有18盏绿灯。
10.72
【分析】因为用会员卡买药可打九五折(九五折=95%),所以得到这瓶药原价的(1-95%)是3.6元,已知一个数的百分之几是多少,用除法,据此列式求出原价是多少元。
【详解】九五折=95%
3.6÷(1-95%)
=3.6÷5%
=3.6÷0.05
=72(元)
故这瓶药原价是72元。
11. 351.68 502.4
【分析】根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算求出这个圆柱的表面积。
根据圆柱的体积公式V=πr2h,代入数据计算求出这个圆柱的体积。
【详解】1dm=10cm
表面积:
3.14×8×10+3.14×(8÷2)2×2
=251.2+3.14×42×2
=251.2+3.14×16×2
=251.2+100.48
=351.68(cm2)
体积:
3.14×(8÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(cm3)
这个圆柱表面积是351.68cm2,体积是502.4cm3。
12. /0.5
【分析】把运来苹果的质量看作单位“1”,已知运来梨的吨数是苹果的,用运来的苹果质量乘就是运来梨的质量,再把运来两种质量的水果相加即可求出总数。
【详解】×=(吨)
+=(吨)
运来梨吨,运来的苹果和梨一共吨。
13.√
【分析】已知段数-1=锯的次数,把一根木棒截成7段,那么就是要截6次才会有7段,用9÷6即可求出每截一次所要花费的时间,现在截成2段,那么只需截1次即可。
【详解】9÷(7-1)
=9÷6
=1.5(分钟)
把这根木棒截成两段,需要1.5分钟。原题干说法正确。
故答案为:√
【点睛】本题关键是求出每截一次所要花费的时间,明确段数和截的次数之间的关系。
14.√
【分析】小刚站在小明北偏东45°方向处,是以小明为观测点;小明在小刚的方向是以小刚为观测点;观测点不同,方向相反,夹角的度数相同,距离相同;由此判断。
【详解】90°-45°=45°
如果小刚站在小明北偏东45°方向处,那么小明就在小刚南偏西45°或西偏南45°的方向处。
原题说法正确。
故答案为:√
【点睛】本题考查位置的相对性,明确同一位置可以用不同的方向和夹角来描述。
15.√
【分析】同一个平面内的两条直线的位置关系只有两种:平行、相交(重合视为同一条直线)。当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫做它们的交点。
【详解】根据两直线相交的概念可知:同一平面内的两条直线相交,只有一个交点。即原题说法正确。
故答案为:√
【点睛】两条不同的直线不能有两个或两个以上的公共点,如果有两个公共点,那么这两条直线就互相重合。
16.√
【分析】根据圆柱的高:h=V÷S,圆锥的高:h=3V÷S,据此可知,如果圆柱和圆锥等底等体积,则圆锥的高是圆柱的高的3倍,据此解答。
【详解】根据分析可知,总体积不变,把一个圆柱形橡皮泥揉成与它等底的圆锥,高将扩大到原来的3倍。原题干说法正确。
故答案为:√
【点睛】本题考查了圆柱和圆锥的体积公式的灵活应用,要熟练掌握公式。
17.√
【分析】根据题意,用结果2(a+5)减去(2a+5),再化简即可。
【详解】2(a+5)-(2a+5)
=2a+10-2a-5
=10-5
=5
所以2a+5错写成2(a+5),结果比原来多5。原题干说法正确。
故答案为:√
【点睛】本题考查了用字母表示数以及含未知数式子的化简。
18.×
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。根据题意可知,白球的个数最多,所以摸到白球的可能性最大,据此解答。
【详解】5>3>2
摸到白球的可能性>摸到黄球的可能性>摸到蓝球的可能性
所以摸到的白球的可能性最大。原题干说法错误。
故答案为:×
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
19.;0.36;;
25;9;0.7;
【详解】略
20.;
;13
【分析】×+÷5,把除法换算成乘法,原式化为:×+×,再根据乘法分配律,原式化为:(+)×,再进行计算;
÷×,把除法换算成乘法,原式化为:××,约分,再进行计算;
÷[×(1-)],先计算小括号里的减法,再计算中括号里的乘法,再计算括号外的除法;
56×(-),根据乘法分配律,原式化为:56×-56×,再进行计算;
【详解】×+÷5
=×+×
=(+)×
=1×
=
÷×
=××
=
=
÷[×(1-)]
=÷[×]
=÷
=×
=
56×(-)
=56×-56×
=48-35
=13
21.;;
【分析】(1)先根据比例的基本性质,把转化成;再根据等式的性质2,在方程两边同时除以1.5;最后根据等式的性质1,在方程两边同时加上2。
(2)先计算=;再根据等式的性质2,在方程两边同时除以。
(3)根据等式的性质2,在方程两边同时乘。
【详解】
解:
(+)=35%
解:
解:
22.平方厘米
【分析】如图,通过割补可知阴影部分面积等于半径为6厘米圆面积的。根据,代入数据计算即可。
【详解】(平方厘米)
即阴影部分面积是平方厘米。
23.小时
【分析】把A、B两地的距离看作单位“1”,甲车行驶全程用了(4+5)小时,根据“速度=路程÷时间”即可求出甲车的速度;
已知两车4小时相遇,根据“速度和=路程÷相遇时间”,求出两车的速度和,再减去甲车的速度,即是乙车的速度;
根据“路程=速度×时间”,求出乙车行驶4小时的路程,用全程减去乙车4小时行驶的路程,即是乙车剩下的路程,再除以乙车的速度,求出乙车到达A地还需要的时间。
【详解】甲车的速度:
1÷(4+5)
=1÷9
=
两车的速度之和:1÷4=
乙车的速度:
-
=-
=
乙车4小时行驶:×4=
乙车到达A地还需的时间:
(1-)÷
=×
=(小时)
答:乙车又行小时到达地。
24.4小时
【分析】根据题意可知,先求出徒弟的工作效率,即,再根据工作时间工作量工作效率和,即可解答。
【详解】=40(个
440÷(40+70)
=440÷110
=4(小时)
答:师徒两人4小时后完成加工任务。
25.27千克
【分析】把原来平均每天产生垃圾的重量看作单位“1”,现在平均每天产生垃圾的重量是原来平均每天产生垃圾重量的(1-10%),求现在平均每天产生垃圾的重量,用原来平均每天产生垃圾的重量×(1-10%)解答,即30×(1-10%)。
【详解】30×(1-10%)
=30×90%
=27(千克)
答:现在平均每天产生垃圾27千克。
26.210个
【分析】把收集到塑料瓶的个数看作单位“1”,用收集到塑料瓶的数量乘,计算出收集的易拉罐的个数,再把易拉罐和塑料瓶的个数相加即可。
【详解】
=60+150
=210(个
答:六1班同学收集易拉罐和塑料瓶共210个。
27.150.72立方厘米
【分析】如下右图中横向锯两次形成3个小圆柱,则表面积是增加了4个圆柱底面积,据此求出一个底面积是12.56平方厘米,根据圆形面积公式可得:r2=12.56÷3.14=4,因为22=4,所以这个圆柱的半径是2厘米;再根据左图中沿底面直径纵向锯成4块,表面积增加了8个以底面半径和高为边长的长方形,用增加面积192平方厘米除以8求得一个长方形,再除以半径2厘米,求得圆柱的高,最后再用圆柱的体积计算公式求出体积。
【详解】50.24÷4=12.56(平方厘米)
12.56÷3.14=4,22=4,所以这个圆柱的底面半径是2厘米
192÷8÷2
=24÷2
=12(厘米)
3.14×22×12
=12.56×12
=150.72(立方厘米)
答:原来这个圆柱形木块的体积是150.72立方厘米。
【点睛】抓住圆柱的两种切割特点,根据增加的表面积分别求出这个圆柱的底面半径和高是解答的关键。
28.(1)500
(2)380;画图见详解
(3)型号的树种适宜推广;因为它的发芽率最高
【分析】(1)把、、、四种型号的小麦实验种子的总粒数看作单位“1”,首先根据减法的意义,用减法求出型号种子数占实验种子总数的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。
(2)将种子总粒数看作单位“1”,首先根据百分数乘法的意义,型号种子有(粒,其发芽率为,根据求一个数的百分之几是多少,用乘法求出型号种子的发芽的粒数,据此完成条形统计图。
(3)将种子总粒数看作单位“1”,首先根据百分数乘法的意义,分别求出、、的种子粒数,再根据求一个数是另外一个数的百分之几用除法,即用每种种类发芽的种子粒数除以其相应的总数,求出该种种子的发芽率,然后进行比较,选择发芽率高的树种适宜进行推广。据此解答。
【详解】(1)
(粒)
用于实验的型号种子是500粒。
(2)(粒)
(粒)
作图如下:
综上所述:型种子发芽率为,型种子中有380粒发芽。
(3):
:
:×100%
×100%
%
所以确定型号的树种适宜推广,因为它的发芽率最高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初高频考点检测卷-数学六年级下册青岛版
一、选择题
1.下面四个图形中,经过折叠能围成下边正方体纸盒的是( )。
A. B.
C. D.
2.下面的式子中,是方程的是( )。
A.3x+5 B.3y-7<8 C. D.81÷9=9
3.一件商品,提高原价的20%,现在又降价20%,商品现在的价格( )。
A.高于原价 B.等于原价 C.低于原价 D.无法确定
4.下列说法正确的是( )。
A.一个数(0除外)除以假分数,商一定小于被除数
B.把25克盐放入100克水中,盐占盐水质量的20%
C.一根木头锯成3段需要6分,那么锯成6段需要12分
D.甲数比乙数多,乙数就比甲数少
5.有甲、乙两筐苹果,如果从甲筐苹果里取出放入乙筐后,两筐苹果的质量相等,那么原来甲、乙两筐苹果的质量比是( )。
A.4∶3 B.7∶5 C.7∶6 D.3∶4
6.一个长方体的长、宽、高分别为a米、b米、h米,如果高增加2米,新的长方体体积比原来增加( )立方米。
A.2ab B.2abh C.ab(h+2) D.abh+22
二、填空题
7.如果把平均成绩记为0分,﹢9分表示比平均成绩( ),﹣7分表示比平均成绩( ),比平均成绩低3分记作( )分。
8.( )∶12==0.25=( )折=( )(填成数)。
9.有一串彩灯是按2红、3绿、5黄的顺序依次排列的。第27盏彩灯是( )色,前60盏中,有( )盏绿灯。
10.用药店的会员卡买药可打九五折,奶奶用会员卡买了一瓶药,省了3.6元,这瓶药原价( )元。
11.一个圆柱的底面直径是8cm,高为1dm,这个圆柱表面积是( )cm2,体积是( )cm3。
12.商店运来苹果吨,运来梨的吨数是苹果的,运来梨( )吨,运来的苹果和梨一共( )吨。
三、判断题
13.一根木棒截成7段要9分钟,那么把这根木棒截成两段,需要1.5分钟。( )
14.如果小刚站在小明北偏东45°方向处,那么小明就在小刚西偏南45°的方向处。( )
15.同一平面内的两条直线相交,只有一个交点。( )
16.把一个圆柱形橡皮泥揉成与它等底的圆锥,高将扩大到原来的3倍。( )
17.2a+5错写成2(a+5),结果比原来多5。( )
18.从下面的盒子里任意摸出一个球,摸到的黄球的可能性最大。( )
四、计算题
19.直接写得数。
20.用你喜欢的方法计算,看谁算得又对又快。
21.解方程(或比例)。
(+)=35%
22.求图中阴影部分的面积。(单位:厘米)(取)
五、解答题
23.甲、乙两车分别从A、B两地同时出发相对开出,4小时相遇,相遇后两车都以各自原速继续行驶,已知甲车又行驶了5小时到达B地,乙车又行多少时间到达A地?
24.师徒两人同时加工440个零件,已知师傅每小时加工70个,徒弟与师傅的工作效率比是。师徒两人几小时后完成加工任务?
25.某小学原来平均每天产生垃圾30千克,自从开展分类投放垃圾后,现在平均每天少产生的垃圾,现在平均每天产生垃圾多少千克?
26. 2023年6月5日是第50个“世界环境日”,六1班同学开展“爱护环境,从我做起”主题活动。活动中收集到塑料瓶150个,收集的易拉罐个数是塑料瓶的,六班同学收集易拉罐和塑料瓶共多少个?
27.把一个圆柱形木块按两种方式锯开。如果沿底面直径纵向锯成4块(下图左),表面积会增加192平方厘米;如果横向锯两次形成3个小圆柱(下图右),表面积会增加50.24平方厘米,原来这个圆柱形木块的体积是多少立方厘米呢?
28.学校农业技术兴趣小组用、、、四种型号的树种共2000粒进行发芽实验。他们根据实验数据正在绘制如图统计图。
(1)观察统计图①,用于做发芽实验的型种子有( )粒。
(2)型种子发芽率为,型种子中有( )粒发芽,将统计图②补充完整。
(3)能不能用这些统计数据来确定哪一种型号的树种适宜推广?简要写出你的想法。
参考答案:
1.B
【分析】
从正方体的纸盒上面的图形可以看成,三个图形不应该是对面。且三角形的一个角对着圆形,据此解答即可。
【详解】
A.三角形和正方形成了对面
B.正好是这三个面
C.三角形和正方形成了对面
D.三角形和圆形成了对面
故答案为:B
2.C
【分析】
含有未知数的等式叫做方程;据此解答。
【详解】A.3x+5,含有未知数,但不是等式,不是方程;
B.3y-7<8,含有未知数,但不是等式,不是方程;
C.,含有未知数,是等式,是方程;
D.81÷9=9,是等式,但不含有未知数,不是方程;
故答案为:C
3.C
【分析】一种商品提价20%,是在原来的价格上提的20%,把原来的价格看作单位“1”,那么提价后的价格是(l+20%),又降价20%,是在提价的基础上降低了20%,此时的单位“1”是提价后的价格,据此求出现价与原价比较即可。
【详解】由分析可知,现价是:
(1+20%)×(1-20%)
=1.2×0.8
=0.96
=96%
商品现在的价格低于原价。
故答案为:C
4.B
【分析】当被除数不等于0时;要弄清楚假分数的数值,分为等于1(分子等于分母)与大于1(分子大于分母)两种情况,进行分类讨论得出答案;
把25克盐放入100克水中,则盐水为25+100克,根据分数的意义,盐占盐水的25÷(100+25);
每次把一根木头可以锯成两段,锯成三段需要锯2次,用6分钟除以2,求出每次需要的时间;锯成6段需要锯5次,用每次需要的时间乘5即可求解;
根据“甲数比乙数多”知道是把乙数看作单位“1”,即甲数(1+),然后用两数的差除以甲数,即可得出乙数比甲数少几分之几,然后比较即可判断。
【详解】A.被除数不是0时;当假分数的数值等于1时,一个数(0除外)除以假分数,所得的商等于这个数;当假分数的数值大于1时,一个数(0除外)除以假分数(乘以真分数),所得的商小于这个数;所以一个数除以假分数,商可能小于被除数,也可能等于被除数;原题说法错误;
B.25÷(100+25)×100%
=25÷125×100%
=0.2×100%
=20%,盐占盐水的20%;原题说法正确;
C.6÷(3-1)×(6-1)
=6÷2×5
=3×5
=15(分钟)把它锯成6段需要15分钟,原题说法错误;
D.÷(1+)
=÷
=×
=,原题说法错误;
故答案为:B
5.B
【分析】根据分数的意义,甲筐苹果平均分成7份,取出1份后甲筐中则有份,乙筐得到1份后和甲筐同样多,也是6份,那么乙筐中原有份,从而求得。
【详解】根据分析可知:
原来甲、乙两筐苹果的质量比是7∶5
故答案为:B
6.A
【分析】
根据题意可知,长、宽不变,高增加2米,所以增加的体积是长为a米、宽为b米、高为2米的长方体,根据长方体的体积=长×宽×高,用a×b×2即可求出增加的体积。
【详解】a×b×2=2ab(立方米)
新的长方体体积比原来增加2ab立方米。
故答案为:A
7. 高9分 低7分 ﹣3
【分析】正负数可以表示相反意义的量,以平均成绩为标准,高于平均成绩记为正,低于平均成绩记为负,据此分析。
【详解】如果把平均成绩记为0分,﹢9分表示比平均成绩高9分,﹣7分表示比平均成绩低7分,比平均成绩低3分记作﹣3分。
8.3;5;二五;二成五
【分析】分数的分子相当于比的前项,分母相当于比的后项,分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。据此先将小数化成分数,根据分数与比的关系,以及它们通用的基本性质进行填空,小数化百分数,小数点向右移动两位,添上百分号即可,根据几折就是百分之几十,几成就是百分之几十,确定折数和成数。
【详解】0.25=,12÷4×1=3;20÷4×1=5;0.25=25%=二五折=二成五
3∶12==0.25=二五折=二成五
9. 黄 18
【分析】这串彩灯按照颜色特点排列的规律是:10盏灯一个循环周期,分别按照:2红、3绿、5黄的顺序依次循环排列;用27除以10所得商为循环了几个周期,余数则为这几盏灯;用60除以10所得商为循环了几个周期,每一个循环周期中有3盏绿灯,用3乘循环的周期,所得结果即为绿灯的数量。
【详解】2+3+5=10(盏)
27÷10=2(个)……7(盏)
第7盏灯是黄色。
60÷10×3
=6×3
=18(盏)
因此第27盏彩灯是黄色,前60盏中,有18盏绿灯。
10.72
【分析】因为用会员卡买药可打九五折(九五折=95%),所以得到这瓶药原价的(1-95%)是3.6元,已知一个数的百分之几是多少,用除法,据此列式求出原价是多少元。
【详解】九五折=95%
3.6÷(1-95%)
=3.6÷5%
=3.6÷0.05
=72(元)
故这瓶药原价是72元。
11. 351.68 502.4
【分析】根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算求出这个圆柱的表面积。
根据圆柱的体积公式V=πr2h,代入数据计算求出这个圆柱的体积。
【详解】1dm=10cm
表面积:
3.14×8×10+3.14×(8÷2)2×2
=251.2+3.14×42×2
=251.2+3.14×16×2
=251.2+100.48
=351.68(cm2)
体积:
3.14×(8÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(cm3)
这个圆柱表面积是351.68cm2,体积是502.4cm3。
12. /0.5
【分析】把运来苹果的质量看作单位“1”,已知运来梨的吨数是苹果的,用运来的苹果质量乘就是运来梨的质量,再把运来两种质量的水果相加即可求出总数。
【详解】×=(吨)
+=(吨)
运来梨吨,运来的苹果和梨一共吨。
13.√
【分析】已知段数-1=锯的次数,把一根木棒截成7段,那么就是要截6次才会有7段,用9÷6即可求出每截一次所要花费的时间,现在截成2段,那么只需截1次即可。
【详解】9÷(7-1)
=9÷6
=1.5(分钟)
把这根木棒截成两段,需要1.5分钟。原题干说法正确。
故答案为:√
【点睛】本题关键是求出每截一次所要花费的时间,明确段数和截的次数之间的关系。
14.√
【分析】小刚站在小明北偏东45°方向处,是以小明为观测点;小明在小刚的方向是以小刚为观测点;观测点不同,方向相反,夹角的度数相同,距离相同;由此判断。
【详解】90°-45°=45°
如果小刚站在小明北偏东45°方向处,那么小明就在小刚南偏西45°或西偏南45°的方向处。
原题说法正确。
故答案为:√
【点睛】本题考查位置的相对性,明确同一位置可以用不同的方向和夹角来描述。
15.√
【分析】同一个平面内的两条直线的位置关系只有两种:平行、相交(重合视为同一条直线)。当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫做它们的交点。
【详解】根据两直线相交的概念可知:同一平面内的两条直线相交,只有一个交点。即原题说法正确。
故答案为:√
【点睛】两条不同的直线不能有两个或两个以上的公共点,如果有两个公共点,那么这两条直线就互相重合。
16.√
【分析】根据圆柱的高:h=V÷S,圆锥的高:h=3V÷S,据此可知,如果圆柱和圆锥等底等体积,则圆锥的高是圆柱的高的3倍,据此解答。
【详解】根据分析可知,总体积不变,把一个圆柱形橡皮泥揉成与它等底的圆锥,高将扩大到原来的3倍。原题干说法正确。
故答案为:√
【点睛】本题考查了圆柱和圆锥的体积公式的灵活应用,要熟练掌握公式。
17.√
【分析】根据题意,用结果2(a+5)减去(2a+5),再化简即可。
【详解】2(a+5)-(2a+5)
=2a+10-2a-5
=10-5
=5
所以2a+5错写成2(a+5),结果比原来多5。原题干说法正确。
故答案为:√
【点睛】本题考查了用字母表示数以及含未知数式子的化简。
18.×
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。根据题意可知,白球的个数最多,所以摸到白球的可能性最大,据此解答。
【详解】5>3>2
摸到白球的可能性>摸到黄球的可能性>摸到蓝球的可能性
所以摸到的白球的可能性最大。原题干说法错误。
故答案为:×
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
19.;0.36;;
25;9;0.7;
【详解】略
20.;
;13
【分析】×+÷5,把除法换算成乘法,原式化为:×+×,再根据乘法分配律,原式化为:(+)×,再进行计算;
÷×,把除法换算成乘法,原式化为:××,约分,再进行计算;
÷[×(1-)],先计算小括号里的减法,再计算中括号里的乘法,再计算括号外的除法;
56×(-),根据乘法分配律,原式化为:56×-56×,再进行计算;
【详解】×+÷5
=×+×
=(+)×
=1×
=
÷×
=××
=
=
÷[×(1-)]
=÷[×]
=÷
=×
=
56×(-)
=56×-56×
=48-35
=13
21.;;
【分析】(1)先根据比例的基本性质,把转化成;再根据等式的性质2,在方程两边同时除以1.5;最后根据等式的性质1,在方程两边同时加上2。
(2)先计算=;再根据等式的性质2,在方程两边同时除以。
(3)根据等式的性质2,在方程两边同时乘。
【详解】
解:
(+)=35%
解:
解:
22.平方厘米
【分析】如图,通过割补可知阴影部分面积等于半径为6厘米圆面积的。根据,代入数据计算即可。
【详解】(平方厘米)
即阴影部分面积是平方厘米。
23.小时
【分析】把A、B两地的距离看作单位“1”,甲车行驶全程用了(4+5)小时,根据“速度=路程÷时间”即可求出甲车的速度;
已知两车4小时相遇,根据“速度和=路程÷相遇时间”,求出两车的速度和,再减去甲车的速度,即是乙车的速度;
根据“路程=速度×时间”,求出乙车行驶4小时的路程,用全程减去乙车4小时行驶的路程,即是乙车剩下的路程,再除以乙车的速度,求出乙车到达A地还需要的时间。
【详解】甲车的速度:
1÷(4+5)
=1÷9
=
两车的速度之和:1÷4=
乙车的速度:
-
=-
=
乙车4小时行驶:×4=
乙车到达A地还需的时间:
(1-)÷
=×
=(小时)
答:乙车又行小时到达地。
24.4小时
【分析】根据题意可知,先求出徒弟的工作效率,即,再根据工作时间工作量工作效率和,即可解答。
【详解】=40(个
440÷(40+70)
=440÷110
=4(小时)
答:师徒两人4小时后完成加工任务。
25.27千克
【分析】把原来平均每天产生垃圾的重量看作单位“1”,现在平均每天产生垃圾的重量是原来平均每天产生垃圾重量的(1-10%),求现在平均每天产生垃圾的重量,用原来平均每天产生垃圾的重量×(1-10%)解答,即30×(1-10%)。
【详解】30×(1-10%)
=30×90%
=27(千克)
答:现在平均每天产生垃圾27千克。
26.210个
【分析】把收集到塑料瓶的个数看作单位“1”,用收集到塑料瓶的数量乘,计算出收集的易拉罐的个数,再把易拉罐和塑料瓶的个数相加即可。
【详解】
=60+150
=210(个
答:六1班同学收集易拉罐和塑料瓶共210个。
27.150.72立方厘米
【分析】如下右图中横向锯两次形成3个小圆柱,则表面积是增加了4个圆柱底面积,据此求出一个底面积是12.56平方厘米,根据圆形面积公式可得:r2=12.56÷3.14=4,因为22=4,所以这个圆柱的半径是2厘米;再根据左图中沿底面直径纵向锯成4块,表面积增加了8个以底面半径和高为边长的长方形,用增加面积192平方厘米除以8求得一个长方形,再除以半径2厘米,求得圆柱的高,最后再用圆柱的体积计算公式求出体积。
【详解】50.24÷4=12.56(平方厘米)
12.56÷3.14=4,22=4,所以这个圆柱的底面半径是2厘米
192÷8÷2
=24÷2
=12(厘米)
3.14×22×12
=12.56×12
=150.72(立方厘米)
答:原来这个圆柱形木块的体积是150.72立方厘米。
【点睛】抓住圆柱的两种切割特点,根据增加的表面积分别求出这个圆柱的底面半径和高是解答的关键。
28.(1)500
(2)380;画图见详解
(3)型号的树种适宜推广;因为它的发芽率最高
【分析】(1)把、、、四种型号的小麦实验种子的总粒数看作单位“1”,首先根据减法的意义,用减法求出型号种子数占实验种子总数的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。
(2)将种子总粒数看作单位“1”,首先根据百分数乘法的意义,型号种子有(粒,其发芽率为,根据求一个数的百分之几是多少,用乘法求出型号种子的发芽的粒数,据此完成条形统计图。
(3)将种子总粒数看作单位“1”,首先根据百分数乘法的意义,分别求出、、的种子粒数,再根据求一个数是另外一个数的百分之几用除法,即用每种种类发芽的种子粒数除以其相应的总数,求出该种种子的发芽率,然后进行比较,选择发芽率高的树种适宜进行推广。据此解答。
【详解】(1)
(粒)
用于实验的型号种子是500粒。
(2)(粒)
(粒)
作图如下:
综上所述:型种子发芽率为,型种子中有380粒发芽。
(3):
:
:×100%
×100%
%
所以确定型号的树种适宜推广,因为它的发芽率最高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
