小升初常考易错检测卷(含答案)数学六年级下册西师大版
文档属性
| 名称 | 小升初常考易错检测卷(含答案)数学六年级下册西师大版 | 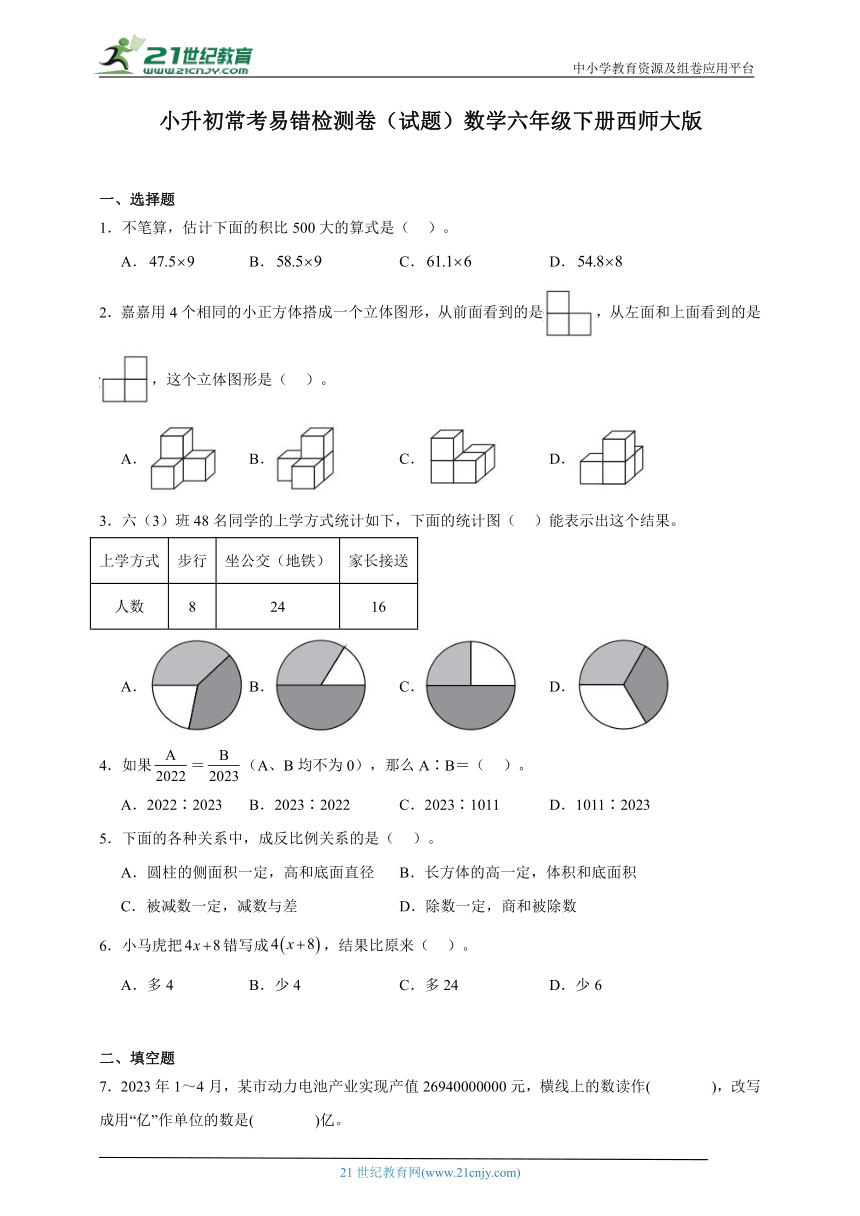 | |
| 格式 | docx | ||
| 文件大小 | 603.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 18:44:15 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
小升初常考易错检测卷(试题)数学六年级下册西师大版
一、选择题
1.不笔算,估计下面的积比500大的算式是( )。
A. B. C. D.
2.嘉嘉用4个相同的小正方体搭成一个立体图形,从前面看到的是,从左面和上面看到的是,这个立体图形是( )。
A. B. C. D.
3.六(3)班48名同学的上学方式统计如下,下面的统计图( )能表示出这个结果。
上学方式 步行 坐公交(地铁) 家长接送
人数 8 24 16
A. B. C. D.
4.如果=(A、B均不为0),那么A∶B=( )。
A.2022∶2023 B.2023∶2022 C.2023∶1011 D.1011∶2023
5.下面的各种关系中,成反比例关系的是( )。
A.圆柱的侧面积一定,高和底面直径 B.长方体的高一定,体积和底面积
C.被减数一定,减数与差 D.除数一定,商和被除数
6.小马虎把错写成,结果比原来( )。
A.多4 B.少4 C.多24 D.少6
二、填空题
7.2023年1~4月,某市动力电池产业实现产值26940000000元,横线上的数读作( ),改写成用“亿”作单位的数是( )亿。
8.6000g=( )kg 2.7L=( )mL 315cm2=( )dm2
9.如果A∶6=B∶7(A≠0,B≠0),那么A∶B=( )∶( )。
10.一根铁丝刚好围成边长分别为7cm,8cm,9cm的三角形,若围成一个圆,这个圆的周长是( )cm,围成一个正方形,这个正方形的面积是( )。
11.在滨海市智轨产业园站上来a名乘客去高铁西站,票价4元;b名乘客去长江桥南站,票价2元。本站本次收入共( )元。
12.笑笑爸爸经营一家烧烤店,美食节第一周共收入8万元,按规定需缴纳5%的营业税,笑笑爸爸需缴纳营业税( )元;爸爸计划将30000元存入银行,定期三年,年利率为2.75%,到期后他可以取回( )元。
三、判断题
13.分母越大,分数单位越小。( )
14.六(1)班同学参加艺体测试,有38人达标,达标率为95%,参加测试的同学有40人。( )
15.找规律:、、、、、、、( ),括号里应填。( )
16.一根光缆线长5m,用去m,还剩2m。( )
17.一个小数的小数点先向左移动两位,再向右移动一位,这个小数缩小为原来的。( )
四、计算题
18.直接写出得数。
3.2÷0.8= 60%+0.3=
120÷6= 20×70= 0×9.2=
19.下列各题怎样简便怎样算。
20.求下列各式中x的值。
21.计算下面阴影部分的面积。(单位:米)(π取3.14)
五、解答题
22.小东和小明共有故事书54本,小东故事书本数的和小明故事书本数的相等。小东和小明各有故事书多少本?
23.汽车厂计划生产汽车800辆,已经生产了一周(7天),平均每天生产60辆。剩下的要5天完成,平均每天需生产多少辆?
24.如图中的三个小圆分别以三角形的三个顶点A、B、C为圆心,并且半径都是4厘米。图中阴影部分的面积之和是多少平方厘米?
25.有甲、乙两个圆柱形容器,从里面量得它们的半径分别是10厘米和5厘米,两个容器的水深分别是10厘米和15厘米。
(1)甲、乙两个容器分别装有多少毫升的水?
(2)如果将乙容器中的一部分水倒入甲容器,使得两个容器的水面一样高。这时水深为多少厘米?
26.某次测试中,甲、乙两名同学的分数比为5∶4,如果甲少得25分,乙多得25分,那么他们的分数比是5∶7,这次测试中,甲、乙原来各得了多少分?
27.在“2023年打击电信网络诈骗犯罪行动”中,我国有23个部门和单位联手打击显成效。学校开展“防止电信网络诈骗”的调查活动。同学们将调查结果整理分析后,正在绘制统计图。
(1)学校共调查了( )人。
(2)请将两幅统计图补充完整。
(3)防止网络诈骗,你想对你身边的人说些什么?
参考答案:
1.B
【分析】运用估算法把各选项算式中的乘数化为整数(或整十数),再求出四个选项估算的乘积,然后与500比较;据此解答。
【详解】A.47.5×9≈47.5×10=475
B.58.5×9≈58.5×10=585
C.61.6×6≈60×6=360
D.54.8×8≈50×8=400
可得:585>500,即58.5×9的积大于500。
故答案为:B
2.C
【分析】从不同方向观察这四个立体图形,分别得出从前面、左面、上面看到的平面图形,再与原图形比较,找出符合要求的立体图形。
【详解】从前面、左面、上面分别看到的平面图形如下:
A.
B.
C.
D.
故答案为:C
3.B
【分析】先求出总人数,用每一部分的人数÷总人数×100%求出每一种上学方式所占总人数的百分比,再依据数据筛选合适的扇形统计图。
【详解】8+24+16=32+16=48(人)
8÷48×100%≈0.17×100%=17%
24÷48×100%=0.5×100%=50%
16÷48×100%≈0.33×100%=33%
50%占整个圆的一半,答案在B和C中,且步行与家长接送所占的百分比不相同,所以表示的比较准确。
故答案为:B
4.A
【分析】根据比例的基本性质“两个外项的积等于两个内项的积”,先将比例式改写成乘法的形式,再将其改写成A∶B的比例式即可。
【详解】由=可得:2023A=2022B;
那么A∶B=2022∶2023。
故答案为:A
5.A
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.根据圆柱的侧面积公式S=πdh可知,圆柱的侧面积一定,即乘积一定,则高和底面直径成反比例关系;
B.根据长方体的体积=底面积×高可得,长方体的体积÷底面积=高(一定),即商一定,则体积和底面积成正比例关系;
C.差+减数=被减数(一定),和一定,则减数与差不成比例;
D.=除数(一定),比值一定,则商和被除数成正比例关系。
故答案为:A
6.C
【分析】用减去,即可得出结果比原来多的部分。
【详解】
结果比原来多24。
故答案为:C
【点睛】本题考查含字母式子的化简与求值,解答本题的关键是掌握含字母式子的化简与求值的计算方法。
7. 二百六十九亿四千万 269.4
【分析】整数的读法:从高位到低位,一级一级往下读,读亿级、万级时要按照个级的读法来读,再在后面加上“亿”或“万”字,每级末尾的0都不读,其他数位上有一个0或连续几个0都只读一个零;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“亿”字。
【详解】26940000000读作二百六十九亿四千万,改写成用“亿”作单位的数是269.4亿。
8. 6 2700 3.15
【分析】高级单位变低级单位用乘法,乘进率;低级单位变高级单位用除法,除以进率; 1kg=1000g,1L=1000mL,1dm2=100cm2。
【详解】6000÷1000=6(kg)
6000g=6kg;
2.7×1000=2700(mL)
2.7L=2700mL;
315÷100=3.15(dm2)
315cm2=3.15dm2
9. 6 7
【分析】在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质。交换两个内项的位置,两个内项的积不变,两个外项的积还是等于两个内项的积。据此解答。
【详解】根据分析可得:
如果A∶6=B∶7(A≠0,B≠0),那么A∶B=6∶7。
10. 24 36
【分析】根据题意可知,先算出铁丝的长度,即为圆的周长。再根据正方形的特征,用铁丝的长度除以4,得出正方形的边长,结合正方形的面积公式:边长×边长,代入数据,计算即可。
【详解】圆的周长:7+8+9
=15+9
=24(cm)
正方形的边长:24÷4=6(cm)
正方形的面积:6×6=36()
所以这个圆的周长是24cm,这个正方形的面积是36。
11.4a+2b/2b+4a
【分析】用去高铁西站的人数乘票价,求出去高铁西站的收入,同理求出去长江桥南站的收入,再把去高铁西站的收入和去长江桥南站的收入相加即可求出本站本次共收入多少元。
【详解】去高铁西站的收入:4×a=4a(元)
去长江桥南站的收入:b×2=2b(元)
所以本站本次共收入(4a+2b)元。
12. 4000 32475
【分析】“第一周的收入×税率=营业税”,“本息=本金+利息=本金+本金×利率×存期”,据此代入数据解答即可。
【详解】8万=80000
80000×5%=4000(元)
30000+30000×2.75%×3
=30000+90000×2.75%
=30000+2475
=32475(元)
所以笑笑爸爸需缴纳营业税4000元,到期后他可以取回32475元。
13.√
【分析】把单位“1”平均分成若干份,表示其中一份的数就是它的分数单位;分子都是1的分数比较大小,分母小的分数大;依此判断。
【详解】
由此可知,分母越大,分数单位越小。
故答案为:√
14.√
【分析】把参加测试的总人数看作单位“1”,根据达标人数÷达标率=总人数,用38÷95%即可求出参加测试的总人数。
【详解】38÷95%=40(人)
根据分析可知,六(1)班同学参加艺体测试,有38人达标,达标率为95%,参加测试的同学有40人,原题干说法正确。
故答案为:√
15.√
【分析】观察可知,分子从1开始不断加1,直到分子只比分母小1,然后分母加1,分母加1后,分子继续从1开始不断加1,直到分子只比分母小1,然后分母加1,据此规律进行分析。
【详解】1+1=2
找规律:、、、、、、、,括号里应填,原题说法正确。
故答案为:√
16.×
【分析】用光缆的长度减去用去的长度,求出剩下的长度,再进行比较,即可解答。
【详解】5-=(m)
一根光缆线长5m,用去m,还剩m。
原题干说法错误。
故答案为:×
17.√
【分析】一个小数的小数点向左移动两位,相当于把原数除以100,小数就缩小到原数的,然后小数点再向右移动一位,相当于再乘10,小数就缩小到原数的,据此判断。
【详解】由分析可知,一个小数的小数点先向左移动两位,再向右移动一位,这个小数缩小为原来的,原题说法正确;
故答案为:√
18.;4;;0.9;
20;1400;;0
【详解】略
19.;;
【分析】(1)先算括号里面的,再算除法,然后算加法。
(2)将2022转化成(2023-1),再利用乘法分配律计算。
(3)将其中一个分数变成,再利用乘法分配律计算。
【详解】(1)
=
=
=
=
(2)
=
=
=
=
(3)
=
=
=
=
20.x=1.25;x=29;x=
【分析】x+x=3.25,先化简方程左边含有x的算式,即求出+1的和,再根据等式的性质2,方程两边同时除以+1的和即可;
(3x-7)×=16,根据等式的性质2,方程两边同时除以,再根据等式的性质1,方程两边同时加上7,再根据等式的性质2,方程两边同时除以3即可;
2∶=x∶,解比例,原式化为:x=2×,再根据等式的性质2,方程两边同时除以即可。
【详解】x+x=3.25
解:x=3.25
x÷=3.25÷
x=3.25×
x=1.25
(3x-7)×=16
解:(3x-7)×÷=16÷
3x-7=16×5
3x-7=80
3x-7+7=80+7
3x=87
3x÷3=87÷3
x=29
2∶=x∶
解:x=2×
x=
x÷=÷
x=×
x=
21.372平方米;114平方米
【分析】第一幅图阴影部分的面积=梯形面积-半圆面积,梯形面积=(上底+下底)×高÷2,半圆面积=圆周率×半径的平方÷2;
第二幅图阴影部分的面积=圆的面积-中间正方形的面积,圆的面积=圆周率×半径的平方,中间正方形可以看成两个等腰直角三角形,三角形的底=大正方形的边长,三角形的高=大正方形的边长÷2,根据三角形面积=底×高÷2,再乘2就是中间正方形的面积。
【详解】(20×2+60)×20÷2-3.14×202÷2
=(40+60)×20÷2-3.14×400÷2
=100×20÷2-628
=1000-628
=372(平方米)
3.14×(20÷2)2-20×(20÷2)÷2×2
=3.14×102-20×10÷2×2
=3.14×100-200
=314-200
=114(平方米)
阴影部分的面积分别是372平方米、114平方米。
22.小东24本;小明30本
【分析】将小东的故事书设为x本,那么小明有故事书(54-x)本。根据“小东故事书本数×=小明故事书本数×”列方程解方程先求出小东的故事书本数,再将总数量减去小东的,求出小明的。
【详解】解:设小东有故事书x本。
x=(54-x)×
x×20=(54-x)××20
5x=216-4x
5x+4x=216-4x+4x
9x=216
9x÷9=216÷9
x=24
54-24=30(本)
答:小东有故事书24本,小明有故事书30本。
23.76辆
【分析】工作效率×工作时间=工作总量,将每天生产60辆乘7天,求出已经生产的数量。将计划生产的总量减去已经生产的,求出剩下的。工作总量÷工作时间=工作效率,将剩下的除以5天,求出平均每天需生产多少辆。
【详解】60×7=420(辆)
800-420=380(辆)
380÷5=76(辆)
答:平均每天需生产76辆。
24.25.12平方厘米
【分析】三个阴影部分的圆心角分别是三角形的三个内角,三角形的内角和是180°,则三个阴影部分的圆心角之和是180°。因为三个小圆的半径都是4厘米,这三个阴影部分合起来就是一个以4厘米为半径的扇形。扇形的面积=πr2×,据此解答。
【详解】3.14×42×
=3.14×16×
=25.12(平方厘米)
答:图中阴影部分的面积之和是25.12平方厘米。
25.(1)3140毫升;1177.5毫升
(2)11厘米
【分析】(1)圆柱形容器中水的体积取决于容器的底面积和水的深度。底面积通过圆的面积公式(S=π×r )计算得出,其中r为半径。甲容器的半径为10厘米,所以底面积为3.14×10×10=314 平方厘米。已知水深为10厘米,体积则是底面积乘水深,即 314×10=3140立方厘米。1立方厘米等于 1 毫升,甲容器中水的体积为3140毫升。
乙容器同理,半径为5厘米,底面积为3.14×5×5=78.5平方厘米,水深15厘米,体积为78.5×15=1177.5 立方厘米,即1177.5毫升。
(2)首先分别求出甲、乙两个容器的底面积。甲容器底面积为314平方厘米,乙容器底面积为78.5平方厘米。然后计算水的总体积,即甲容器中水的体积3140立方厘米加上乙容器中水的体积1177.5立方厘米,得到4317.5立方厘米。要使两个容器的水面高度相同,那么水的总体积不变,将总体积按照两个容器底面积的比例进行分配,就能得到相同的水深。也就是用总体积除两个容器底面积之和,就可以得出此时的水深。
【详解】(1)甲容器的半径为10厘米,底面积为:3.14×10×10 = 314(平方厘米)
水深10厘米,体积为:314×10=3140(立方厘米)
因为1立方厘米=1毫升,所以甲容器水的体积为3140毫升。
乙容器的半径为5厘米,底面积为:3.14×5×5=78.5(平方厘米)
水深15厘米,体积为:78.5×15 = 1177.5立方厘米=1177.5毫升
乙容器水的体积为1177.5毫升。
答:甲容器装有3140毫升水,乙容器装有1177.5毫升水。
(2)甲容器的底面积为314平方厘米,乙容器的底面积为78.5平方厘米。
水的总体积为:3140+1177.5=4317.5(立方厘米)
两个容器底面积之和为:314+78.5=392.5(平方厘米)
此时水深:4317.5÷392.5=11(厘米)
答:这时水深为11厘米。
26.甲:100分;乙:80分
【分析】设甲得了5x分,则乙得了4x分,如果甲少得25分,乙多得25分,则甲的得分为(5x-25)分,乙的得分为(4x+25)分,根据“如果甲少得25分,乙多得25分,那么他们的分数比是5∶7”列比例解答即可。
【详解】解:设甲得了5x分,则乙得了4x分。
(5x-25)∶(4x+25)=5∶7
(4x+25)×5=(5x-25)×7
20x+125=35x-175
15x=300
x=20
20×5=100(分)
20×4=80(分)
答:甲原来得了100分,乙原来得了80分。
27.(1)200
(2)见详解
(3)见详解
【分析】(1)将调查总人数看作单位“1”,软件诈骗人数÷对应百分率=调查总人数;
(2)调查总人数×虚假中奖对应百分率=虚假中奖人数,总人数-网络诈骗人数-虚假中奖人数-软件诈骗人数=电话欠费人数,据此画出相应直条,标记数据,即可补充条形统计图;
网络诈骗人数÷总人数×100%=网络诈骗对应百分率,电话欠费人数÷总人数×100%=电话欠费对应百分率,据此补充扇形统计图;
(3)答案不唯一,合理即可,如加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电等。
【详解】(1)20÷10%=20÷0.1=200(人)
学校共调查了200人。
(2)200×25%=200×0.25=50(人)
200-90-50-20=40(人)
90÷200×100%
=0.45×100%
=45%
40÷200×100%
=0.2×100%
=20%
(3)为了防止网络诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电,关注国家反诈平台,加强自我道德建设,克服“贪小便宜”、“不劳而获”的思想等。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初常考易错检测卷(试题)数学六年级下册西师大版
一、选择题
1.不笔算,估计下面的积比500大的算式是( )。
A. B. C. D.
2.嘉嘉用4个相同的小正方体搭成一个立体图形,从前面看到的是,从左面和上面看到的是,这个立体图形是( )。
A. B. C. D.
3.六(3)班48名同学的上学方式统计如下,下面的统计图( )能表示出这个结果。
上学方式 步行 坐公交(地铁) 家长接送
人数 8 24 16
A. B. C. D.
4.如果=(A、B均不为0),那么A∶B=( )。
A.2022∶2023 B.2023∶2022 C.2023∶1011 D.1011∶2023
5.下面的各种关系中,成反比例关系的是( )。
A.圆柱的侧面积一定,高和底面直径 B.长方体的高一定,体积和底面积
C.被减数一定,减数与差 D.除数一定,商和被除数
6.小马虎把错写成,结果比原来( )。
A.多4 B.少4 C.多24 D.少6
二、填空题
7.2023年1~4月,某市动力电池产业实现产值26940000000元,横线上的数读作( ),改写成用“亿”作单位的数是( )亿。
8.6000g=( )kg 2.7L=( )mL 315cm2=( )dm2
9.如果A∶6=B∶7(A≠0,B≠0),那么A∶B=( )∶( )。
10.一根铁丝刚好围成边长分别为7cm,8cm,9cm的三角形,若围成一个圆,这个圆的周长是( )cm,围成一个正方形,这个正方形的面积是( )。
11.在滨海市智轨产业园站上来a名乘客去高铁西站,票价4元;b名乘客去长江桥南站,票价2元。本站本次收入共( )元。
12.笑笑爸爸经营一家烧烤店,美食节第一周共收入8万元,按规定需缴纳5%的营业税,笑笑爸爸需缴纳营业税( )元;爸爸计划将30000元存入银行,定期三年,年利率为2.75%,到期后他可以取回( )元。
三、判断题
13.分母越大,分数单位越小。( )
14.六(1)班同学参加艺体测试,有38人达标,达标率为95%,参加测试的同学有40人。( )
15.找规律:、、、、、、、( ),括号里应填。( )
16.一根光缆线长5m,用去m,还剩2m。( )
17.一个小数的小数点先向左移动两位,再向右移动一位,这个小数缩小为原来的。( )
四、计算题
18.直接写出得数。
3.2÷0.8= 60%+0.3=
120÷6= 20×70= 0×9.2=
19.下列各题怎样简便怎样算。
20.求下列各式中x的值。
21.计算下面阴影部分的面积。(单位:米)(π取3.14)
五、解答题
22.小东和小明共有故事书54本,小东故事书本数的和小明故事书本数的相等。小东和小明各有故事书多少本?
23.汽车厂计划生产汽车800辆,已经生产了一周(7天),平均每天生产60辆。剩下的要5天完成,平均每天需生产多少辆?
24.如图中的三个小圆分别以三角形的三个顶点A、B、C为圆心,并且半径都是4厘米。图中阴影部分的面积之和是多少平方厘米?
25.有甲、乙两个圆柱形容器,从里面量得它们的半径分别是10厘米和5厘米,两个容器的水深分别是10厘米和15厘米。
(1)甲、乙两个容器分别装有多少毫升的水?
(2)如果将乙容器中的一部分水倒入甲容器,使得两个容器的水面一样高。这时水深为多少厘米?
26.某次测试中,甲、乙两名同学的分数比为5∶4,如果甲少得25分,乙多得25分,那么他们的分数比是5∶7,这次测试中,甲、乙原来各得了多少分?
27.在“2023年打击电信网络诈骗犯罪行动”中,我国有23个部门和单位联手打击显成效。学校开展“防止电信网络诈骗”的调查活动。同学们将调查结果整理分析后,正在绘制统计图。
(1)学校共调查了( )人。
(2)请将两幅统计图补充完整。
(3)防止网络诈骗,你想对你身边的人说些什么?
参考答案:
1.B
【分析】运用估算法把各选项算式中的乘数化为整数(或整十数),再求出四个选项估算的乘积,然后与500比较;据此解答。
【详解】A.47.5×9≈47.5×10=475
B.58.5×9≈58.5×10=585
C.61.6×6≈60×6=360
D.54.8×8≈50×8=400
可得:585>500,即58.5×9的积大于500。
故答案为:B
2.C
【分析】从不同方向观察这四个立体图形,分别得出从前面、左面、上面看到的平面图形,再与原图形比较,找出符合要求的立体图形。
【详解】从前面、左面、上面分别看到的平面图形如下:
A.
B.
C.
D.
故答案为:C
3.B
【分析】先求出总人数,用每一部分的人数÷总人数×100%求出每一种上学方式所占总人数的百分比,再依据数据筛选合适的扇形统计图。
【详解】8+24+16=32+16=48(人)
8÷48×100%≈0.17×100%=17%
24÷48×100%=0.5×100%=50%
16÷48×100%≈0.33×100%=33%
50%占整个圆的一半,答案在B和C中,且步行与家长接送所占的百分比不相同,所以表示的比较准确。
故答案为:B
4.A
【分析】根据比例的基本性质“两个外项的积等于两个内项的积”,先将比例式改写成乘法的形式,再将其改写成A∶B的比例式即可。
【详解】由=可得:2023A=2022B;
那么A∶B=2022∶2023。
故答案为:A
5.A
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.根据圆柱的侧面积公式S=πdh可知,圆柱的侧面积一定,即乘积一定,则高和底面直径成反比例关系;
B.根据长方体的体积=底面积×高可得,长方体的体积÷底面积=高(一定),即商一定,则体积和底面积成正比例关系;
C.差+减数=被减数(一定),和一定,则减数与差不成比例;
D.=除数(一定),比值一定,则商和被除数成正比例关系。
故答案为:A
6.C
【分析】用减去,即可得出结果比原来多的部分。
【详解】
结果比原来多24。
故答案为:C
【点睛】本题考查含字母式子的化简与求值,解答本题的关键是掌握含字母式子的化简与求值的计算方法。
7. 二百六十九亿四千万 269.4
【分析】整数的读法:从高位到低位,一级一级往下读,读亿级、万级时要按照个级的读法来读,再在后面加上“亿”或“万”字,每级末尾的0都不读,其他数位上有一个0或连续几个0都只读一个零;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“亿”字。
【详解】26940000000读作二百六十九亿四千万,改写成用“亿”作单位的数是269.4亿。
8. 6 2700 3.15
【分析】高级单位变低级单位用乘法,乘进率;低级单位变高级单位用除法,除以进率; 1kg=1000g,1L=1000mL,1dm2=100cm2。
【详解】6000÷1000=6(kg)
6000g=6kg;
2.7×1000=2700(mL)
2.7L=2700mL;
315÷100=3.15(dm2)
315cm2=3.15dm2
9. 6 7
【分析】在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质。交换两个内项的位置,两个内项的积不变,两个外项的积还是等于两个内项的积。据此解答。
【详解】根据分析可得:
如果A∶6=B∶7(A≠0,B≠0),那么A∶B=6∶7。
10. 24 36
【分析】根据题意可知,先算出铁丝的长度,即为圆的周长。再根据正方形的特征,用铁丝的长度除以4,得出正方形的边长,结合正方形的面积公式:边长×边长,代入数据,计算即可。
【详解】圆的周长:7+8+9
=15+9
=24(cm)
正方形的边长:24÷4=6(cm)
正方形的面积:6×6=36()
所以这个圆的周长是24cm,这个正方形的面积是36。
11.4a+2b/2b+4a
【分析】用去高铁西站的人数乘票价,求出去高铁西站的收入,同理求出去长江桥南站的收入,再把去高铁西站的收入和去长江桥南站的收入相加即可求出本站本次共收入多少元。
【详解】去高铁西站的收入:4×a=4a(元)
去长江桥南站的收入:b×2=2b(元)
所以本站本次共收入(4a+2b)元。
12. 4000 32475
【分析】“第一周的收入×税率=营业税”,“本息=本金+利息=本金+本金×利率×存期”,据此代入数据解答即可。
【详解】8万=80000
80000×5%=4000(元)
30000+30000×2.75%×3
=30000+90000×2.75%
=30000+2475
=32475(元)
所以笑笑爸爸需缴纳营业税4000元,到期后他可以取回32475元。
13.√
【分析】把单位“1”平均分成若干份,表示其中一份的数就是它的分数单位;分子都是1的分数比较大小,分母小的分数大;依此判断。
【详解】
由此可知,分母越大,分数单位越小。
故答案为:√
14.√
【分析】把参加测试的总人数看作单位“1”,根据达标人数÷达标率=总人数,用38÷95%即可求出参加测试的总人数。
【详解】38÷95%=40(人)
根据分析可知,六(1)班同学参加艺体测试,有38人达标,达标率为95%,参加测试的同学有40人,原题干说法正确。
故答案为:√
15.√
【分析】观察可知,分子从1开始不断加1,直到分子只比分母小1,然后分母加1,分母加1后,分子继续从1开始不断加1,直到分子只比分母小1,然后分母加1,据此规律进行分析。
【详解】1+1=2
找规律:、、、、、、、,括号里应填,原题说法正确。
故答案为:√
16.×
【分析】用光缆的长度减去用去的长度,求出剩下的长度,再进行比较,即可解答。
【详解】5-=(m)
一根光缆线长5m,用去m,还剩m。
原题干说法错误。
故答案为:×
17.√
【分析】一个小数的小数点向左移动两位,相当于把原数除以100,小数就缩小到原数的,然后小数点再向右移动一位,相当于再乘10,小数就缩小到原数的,据此判断。
【详解】由分析可知,一个小数的小数点先向左移动两位,再向右移动一位,这个小数缩小为原来的,原题说法正确;
故答案为:√
18.;4;;0.9;
20;1400;;0
【详解】略
19.;;
【分析】(1)先算括号里面的,再算除法,然后算加法。
(2)将2022转化成(2023-1),再利用乘法分配律计算。
(3)将其中一个分数变成,再利用乘法分配律计算。
【详解】(1)
=
=
=
=
(2)
=
=
=
=
(3)
=
=
=
=
20.x=1.25;x=29;x=
【分析】x+x=3.25,先化简方程左边含有x的算式,即求出+1的和,再根据等式的性质2,方程两边同时除以+1的和即可;
(3x-7)×=16,根据等式的性质2,方程两边同时除以,再根据等式的性质1,方程两边同时加上7,再根据等式的性质2,方程两边同时除以3即可;
2∶=x∶,解比例,原式化为:x=2×,再根据等式的性质2,方程两边同时除以即可。
【详解】x+x=3.25
解:x=3.25
x÷=3.25÷
x=3.25×
x=1.25
(3x-7)×=16
解:(3x-7)×÷=16÷
3x-7=16×5
3x-7=80
3x-7+7=80+7
3x=87
3x÷3=87÷3
x=29
2∶=x∶
解:x=2×
x=
x÷=÷
x=×
x=
21.372平方米;114平方米
【分析】第一幅图阴影部分的面积=梯形面积-半圆面积,梯形面积=(上底+下底)×高÷2,半圆面积=圆周率×半径的平方÷2;
第二幅图阴影部分的面积=圆的面积-中间正方形的面积,圆的面积=圆周率×半径的平方,中间正方形可以看成两个等腰直角三角形,三角形的底=大正方形的边长,三角形的高=大正方形的边长÷2,根据三角形面积=底×高÷2,再乘2就是中间正方形的面积。
【详解】(20×2+60)×20÷2-3.14×202÷2
=(40+60)×20÷2-3.14×400÷2
=100×20÷2-628
=1000-628
=372(平方米)
3.14×(20÷2)2-20×(20÷2)÷2×2
=3.14×102-20×10÷2×2
=3.14×100-200
=314-200
=114(平方米)
阴影部分的面积分别是372平方米、114平方米。
22.小东24本;小明30本
【分析】将小东的故事书设为x本,那么小明有故事书(54-x)本。根据“小东故事书本数×=小明故事书本数×”列方程解方程先求出小东的故事书本数,再将总数量减去小东的,求出小明的。
【详解】解:设小东有故事书x本。
x=(54-x)×
x×20=(54-x)××20
5x=216-4x
5x+4x=216-4x+4x
9x=216
9x÷9=216÷9
x=24
54-24=30(本)
答:小东有故事书24本,小明有故事书30本。
23.76辆
【分析】工作效率×工作时间=工作总量,将每天生产60辆乘7天,求出已经生产的数量。将计划生产的总量减去已经生产的,求出剩下的。工作总量÷工作时间=工作效率,将剩下的除以5天,求出平均每天需生产多少辆。
【详解】60×7=420(辆)
800-420=380(辆)
380÷5=76(辆)
答:平均每天需生产76辆。
24.25.12平方厘米
【分析】三个阴影部分的圆心角分别是三角形的三个内角,三角形的内角和是180°,则三个阴影部分的圆心角之和是180°。因为三个小圆的半径都是4厘米,这三个阴影部分合起来就是一个以4厘米为半径的扇形。扇形的面积=πr2×,据此解答。
【详解】3.14×42×
=3.14×16×
=25.12(平方厘米)
答:图中阴影部分的面积之和是25.12平方厘米。
25.(1)3140毫升;1177.5毫升
(2)11厘米
【分析】(1)圆柱形容器中水的体积取决于容器的底面积和水的深度。底面积通过圆的面积公式(S=π×r )计算得出,其中r为半径。甲容器的半径为10厘米,所以底面积为3.14×10×10=314 平方厘米。已知水深为10厘米,体积则是底面积乘水深,即 314×10=3140立方厘米。1立方厘米等于 1 毫升,甲容器中水的体积为3140毫升。
乙容器同理,半径为5厘米,底面积为3.14×5×5=78.5平方厘米,水深15厘米,体积为78.5×15=1177.5 立方厘米,即1177.5毫升。
(2)首先分别求出甲、乙两个容器的底面积。甲容器底面积为314平方厘米,乙容器底面积为78.5平方厘米。然后计算水的总体积,即甲容器中水的体积3140立方厘米加上乙容器中水的体积1177.5立方厘米,得到4317.5立方厘米。要使两个容器的水面高度相同,那么水的总体积不变,将总体积按照两个容器底面积的比例进行分配,就能得到相同的水深。也就是用总体积除两个容器底面积之和,就可以得出此时的水深。
【详解】(1)甲容器的半径为10厘米,底面积为:3.14×10×10 = 314(平方厘米)
水深10厘米,体积为:314×10=3140(立方厘米)
因为1立方厘米=1毫升,所以甲容器水的体积为3140毫升。
乙容器的半径为5厘米,底面积为:3.14×5×5=78.5(平方厘米)
水深15厘米,体积为:78.5×15 = 1177.5立方厘米=1177.5毫升
乙容器水的体积为1177.5毫升。
答:甲容器装有3140毫升水,乙容器装有1177.5毫升水。
(2)甲容器的底面积为314平方厘米,乙容器的底面积为78.5平方厘米。
水的总体积为:3140+1177.5=4317.5(立方厘米)
两个容器底面积之和为:314+78.5=392.5(平方厘米)
此时水深:4317.5÷392.5=11(厘米)
答:这时水深为11厘米。
26.甲:100分;乙:80分
【分析】设甲得了5x分,则乙得了4x分,如果甲少得25分,乙多得25分,则甲的得分为(5x-25)分,乙的得分为(4x+25)分,根据“如果甲少得25分,乙多得25分,那么他们的分数比是5∶7”列比例解答即可。
【详解】解:设甲得了5x分,则乙得了4x分。
(5x-25)∶(4x+25)=5∶7
(4x+25)×5=(5x-25)×7
20x+125=35x-175
15x=300
x=20
20×5=100(分)
20×4=80(分)
答:甲原来得了100分,乙原来得了80分。
27.(1)200
(2)见详解
(3)见详解
【分析】(1)将调查总人数看作单位“1”,软件诈骗人数÷对应百分率=调查总人数;
(2)调查总人数×虚假中奖对应百分率=虚假中奖人数,总人数-网络诈骗人数-虚假中奖人数-软件诈骗人数=电话欠费人数,据此画出相应直条,标记数据,即可补充条形统计图;
网络诈骗人数÷总人数×100%=网络诈骗对应百分率,电话欠费人数÷总人数×100%=电话欠费对应百分率,据此补充扇形统计图;
(3)答案不唯一,合理即可,如加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电等。
【详解】(1)20÷10%=20÷0.1=200(人)
学校共调查了200人。
(2)200×25%=200×0.25=50(人)
200-90-50-20=40(人)
90÷200×100%
=0.45×100%
=45%
40÷200×100%
=0.2×100%
=20%
(3)为了防止网络诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电,关注国家反诈平台,加强自我道德建设,克服“贪小便宜”、“不劳而获”的思想等。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
