14.2勾股定理的应用 第2课时 课件(共19张PPT)2024-2025学年华东师大版八年级数学上册
文档属性
| 名称 | 14.2勾股定理的应用 第2课时 课件(共19张PPT)2024-2025学年华东师大版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
14.2 勾股定理的应用第2课时
基础 主干落实
重点 典例研析
素养 当堂测评
基础 主干落实
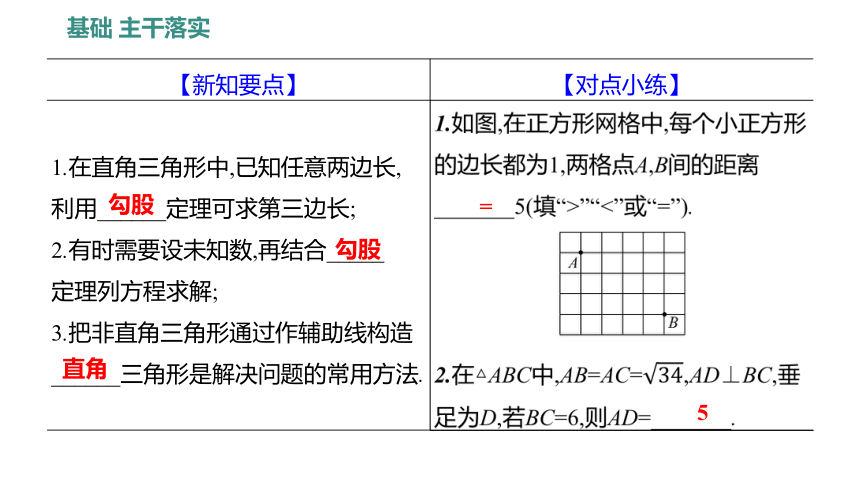
【新知要点】 【对点小练】
1.在直角三角形中,已知任意两边长, 利用______定理可求第三边长; 2.有时需要设未知数,再结合_____ 定理列方程求解; 3.把非直角三角形通过作辅助线构造 ______三角形是解决问题的常用方法. 1.如图,在正方形网格中,每个小正方形
的边长都为1,两格点A,B间的距离
_______5(填“>”“<”或“=”).
2.在△ABC中,AB=AC=,AD⊥BC,垂
足为D,若BC=6,则AD=_______.
勾股
勾股
直角
=
5
重点 典例研析
重点1 网格中的相关计算(几何直观、运算能力)
【典例1】(教材再开发·P122例3拓展)如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
【自主解答】(1)S△ABC=4×8-3×2÷2-1×8÷2-4×6÷2=32-3-4-12=13,
故△ABC的面积为13;
【典例1】(教材再开发·P122例3拓展)如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(2)判断△ABC是什么形状,并说明理由.
【自主解答】(2)△ABC是直角三角形,理由如下:
∵小方格边长为1,
∴AB2=22+32=13,
AC2=12+82=65,
BC2=62+42=52,
∴AB2+BC2=AC2,
∴△ABC为直角三角形.
【举一反三】
(2024·绵阳期末)如图,是直角三角形的是 ( )
A.① B.②
C.③ D.①②
B
【技法点拨】
网格中勾股定理的应用
正方形网格中每一个小正方形的边长为1,然后应用勾股定理计算线段长.
重点2 利用勾股定理及其逆定理进行计算(运算能力、应用意识)
【典例2】(教材再开发·P122例4补充)如图,某小区的两个喷泉的距离AB的长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
【自主解答】(1)在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m),
在Rt△AMN中,AM===200(m),
∴供水点M到喷泉A,B需要铺设的管道总长为200+150=350(m);
【典例2】(教材再开发·P122例4补充)如图,某小区的两个喷泉的距离AB的长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.
(2)直接写出喷泉B到小路AC的最短距离.
【自主解答】(2)∵AB=250 m,AM=200 m,BM=150 m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形,∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150 m.
【举一反三】
如图,在△ABC中,CD⊥AB于点D,BC=15,CD=12,AD=16.
(1)求BD的长;
【解析】(1)∵CD⊥AB,∴∠CDB=90°,
∵BC=15,CD=12,
∴BD===9,
∴BD的长为9;
如图,在△ABC中,CD⊥AB于点D,BC=15,CD=12,AD=16.
(2)求△ABC的面积;
【解析】(2)∵AD=16,BD=9,
∴AB=AD+BD=16+9=25,
∵CD⊥AB,CD=12,
∴S△ABC=AB·CD=×25×12=150,
∴△ABC的面积为150;
如图,在△ABC中,CD⊥AB于点D,BC=15,CD=12,AD=16.
(3)判断△ABC的形状,并说明理由.
【解析】(3)△ABC是直角三角形,理由如下:
在Rt△ACD中,AD=16,CD=12,
∴AC===20,
∵AC2+BC2=202+152=625,AB2=252=625,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
【技法点拨】
勾股定理的应用
1.关于非直角三角形的计算往往需要作辅助线构造直角三角形,然后用勾股定理来解决.
2.勾股定理常常与平方差公式、两数和(差)的平方公式结合使用.
素养 当堂测评
1.(3分·几何直观)如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以O为
圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是 ( )
A. B.2 C. D.2.5
C
2.(3分·几何直观、运算能力)如图,在△ABC中,∠B=90°,AB=2,BC=4,四边形ADEC是正方形,则正方形ADEC的面积是 ( )
A.8 B.16
C.20 D.25
C
3.(3分·几何直观、运算能力)如图,一个电子跳蚤在4×5的网格(网格中小格子均为边长为1的正方形)中,沿A→B→C→A跳了一圈,它跳的总路程是___________.
7+
4.(4分·推理能力、几何直观)如图,∠BAC=90°,AB=4,AC=4,BD=7,DC=9,则∠DBA=________.
45°
5.(7分·应用意识、运算能力)如图,要修建一个育苗棚,棚高h=5 m,棚宽a=12 m,棚的长d为12 m,现要在棚顶上覆盖塑料薄膜,试求至少需要多少平方米塑料薄膜
【解析】如图,∵h=5 m,a=12 m,
∴AB==13(m),
∴至少需要塑料薄膜13×12=156 m2.
本课结束
14.2 勾股定理的应用第2课时
基础 主干落实
重点 典例研析
素养 当堂测评
基础 主干落实
【新知要点】 【对点小练】
1.在直角三角形中,已知任意两边长, 利用______定理可求第三边长; 2.有时需要设未知数,再结合_____ 定理列方程求解; 3.把非直角三角形通过作辅助线构造 ______三角形是解决问题的常用方法. 1.如图,在正方形网格中,每个小正方形
的边长都为1,两格点A,B间的距离
_______5(填“>”“<”或“=”).
2.在△ABC中,AB=AC=,AD⊥BC,垂
足为D,若BC=6,则AD=_______.
勾股
勾股
直角
=
5
重点 典例研析
重点1 网格中的相关计算(几何直观、运算能力)
【典例1】(教材再开发·P122例3拓展)如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
【自主解答】(1)S△ABC=4×8-3×2÷2-1×8÷2-4×6÷2=32-3-4-12=13,
故△ABC的面积为13;
【典例1】(教材再开发·P122例3拓展)如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(2)判断△ABC是什么形状,并说明理由.
【自主解答】(2)△ABC是直角三角形,理由如下:
∵小方格边长为1,
∴AB2=22+32=13,
AC2=12+82=65,
BC2=62+42=52,
∴AB2+BC2=AC2,
∴△ABC为直角三角形.
【举一反三】
(2024·绵阳期末)如图,是直角三角形的是 ( )
A.① B.②
C.③ D.①②
B
【技法点拨】
网格中勾股定理的应用
正方形网格中每一个小正方形的边长为1,然后应用勾股定理计算线段长.
重点2 利用勾股定理及其逆定理进行计算(运算能力、应用意识)
【典例2】(教材再开发·P122例4补充)如图,某小区的两个喷泉的距离AB的长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
【自主解答】(1)在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m),
在Rt△AMN中,AM===200(m),
∴供水点M到喷泉A,B需要铺设的管道总长为200+150=350(m);
【典例2】(教材再开发·P122例4补充)如图,某小区的两个喷泉的距离AB的长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.
(2)直接写出喷泉B到小路AC的最短距离.
【自主解答】(2)∵AB=250 m,AM=200 m,BM=150 m,
∴AB2=BM2+AM2,
∴△ABM是直角三角形,∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM=150 m.
【举一反三】
如图,在△ABC中,CD⊥AB于点D,BC=15,CD=12,AD=16.
(1)求BD的长;
【解析】(1)∵CD⊥AB,∴∠CDB=90°,
∵BC=15,CD=12,
∴BD===9,
∴BD的长为9;
如图,在△ABC中,CD⊥AB于点D,BC=15,CD=12,AD=16.
(2)求△ABC的面积;
【解析】(2)∵AD=16,BD=9,
∴AB=AD+BD=16+9=25,
∵CD⊥AB,CD=12,
∴S△ABC=AB·CD=×25×12=150,
∴△ABC的面积为150;
如图,在△ABC中,CD⊥AB于点D,BC=15,CD=12,AD=16.
(3)判断△ABC的形状,并说明理由.
【解析】(3)△ABC是直角三角形,理由如下:
在Rt△ACD中,AD=16,CD=12,
∴AC===20,
∵AC2+BC2=202+152=625,AB2=252=625,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
【技法点拨】
勾股定理的应用
1.关于非直角三角形的计算往往需要作辅助线构造直角三角形,然后用勾股定理来解决.
2.勾股定理常常与平方差公式、两数和(差)的平方公式结合使用.
素养 当堂测评
1.(3分·几何直观)如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以O为
圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是 ( )
A. B.2 C. D.2.5
C
2.(3分·几何直观、运算能力)如图,在△ABC中,∠B=90°,AB=2,BC=4,四边形ADEC是正方形,则正方形ADEC的面积是 ( )
A.8 B.16
C.20 D.25
C
3.(3分·几何直观、运算能力)如图,一个电子跳蚤在4×5的网格(网格中小格子均为边长为1的正方形)中,沿A→B→C→A跳了一圈,它跳的总路程是___________.
7+
4.(4分·推理能力、几何直观)如图,∠BAC=90°,AB=4,AC=4,BD=7,DC=9,则∠DBA=________.
45°
5.(7分·应用意识、运算能力)如图,要修建一个育苗棚,棚高h=5 m,棚宽a=12 m,棚的长d为12 m,现要在棚顶上覆盖塑料薄膜,试求至少需要多少平方米塑料薄膜
【解析】如图,∵h=5 m,a=12 m,
∴AB==13(m),
∴至少需要塑料薄膜13×12=156 m2.
本课结束
