图形面积 培优训练(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 图形面积 培优训练(含答案)2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 07:07:58 | ||
图片预览




文档简介
图形面积
一、课标导航
课标内容 课标要求 目标层次
图形面积 掌握基本图形面积的计算公式 ★
计算面积或利用图形面积解决数学问题
二、核心纲要
1.一些常用图形的面积公式
正方形面积=边长×边长; 长方形(矩形)面积=长×宽; 平行四边形面积=底×高;
三角形面积 底×高; 梯形面积 (上底+下底)×高.
2.计算图形的面积有以下常用方法
(1)和差法:把图形面积用常见图形面积的和或差表示,通过常规图形面积公式计算.
(2)割补法:有时直接求图形面积有困难,我们可以通过分割或补形,把图形转化为容易观察或解决的形状求解.
(3)等积变换法:对某些图形,找出与所求图形面积相等或有关联的特殊图形,通过代换转化易求图形的面积.
(4)等比法:将面积比转化为线段比.
3.在两个三角形中
(1)同(等)高时,面积之比等于底之比.(2)同(等)底时,面积之比等于高之比.
4.等分三角形面积
三角形一边中线平分三角形面积.
5.常见的基本模型
若 AD∥BC,则 S△AOB=S△COD,S△ABC=S△BCD
中小学教育资源及组卷应用平台
平行四边形ABCD
本节重点讲解:图形面积的计算和证明.
三、全能突破
基础演练
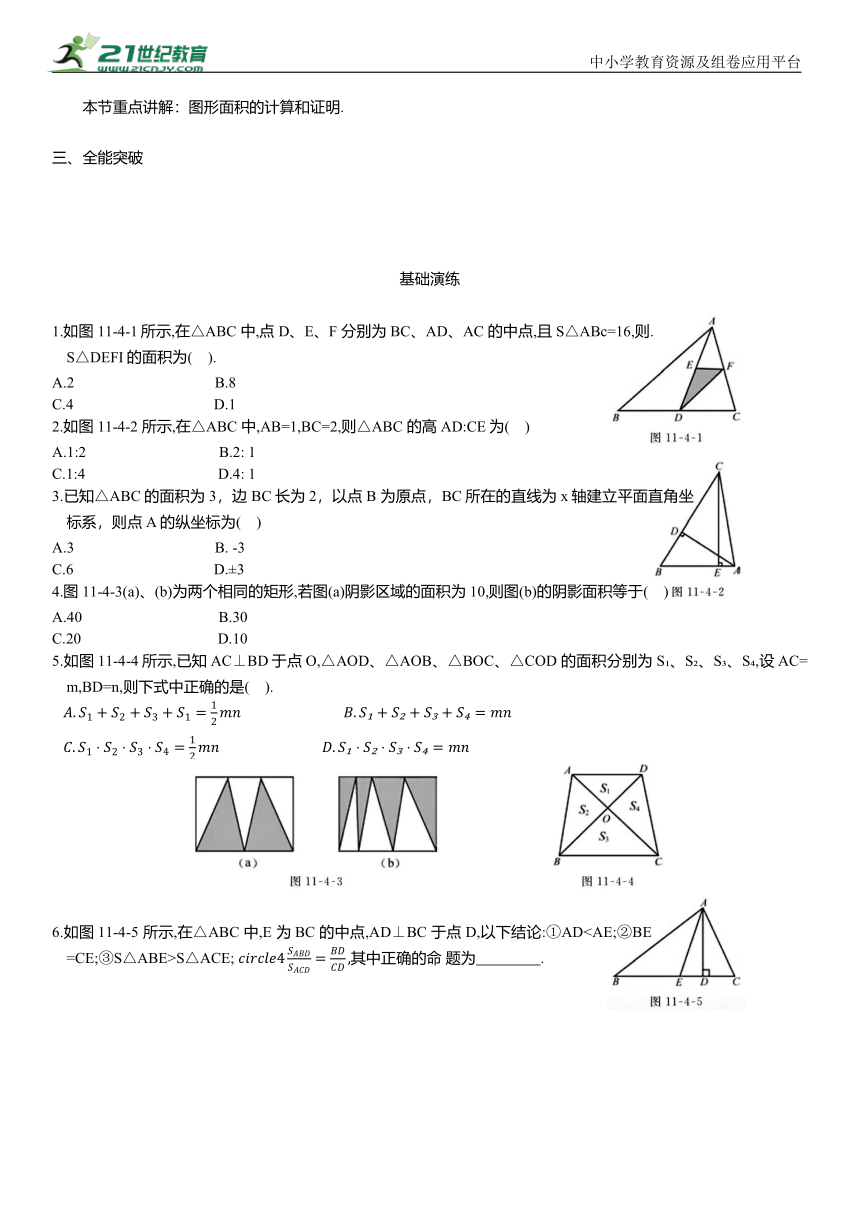
1.如图11-4-1所示,在△ABC 中,点 D、E、F 分别为BC、AD、AC 的中点,且S△ABc=16,则.S△DEFI的面积为( ).
A.2 B.8
C.4 D.1
2.如图11-4-2 所示,在△ABC 中,AB=1,BC=2,则△ABC 的高AD:CE为( )
A.1:2 B.2: 1
C.1:4 D.4: 1
3.已知△ABC的面积为3,边 BC长为2,以点B 为原点,BC所在的直线为x轴建立平面直角坐标系,则点 A的纵坐标为( )
A.3 B. -3
C.6 D.±3
4.图11-4-3(a)、(b)为两个相同的矩形,若图(a)阴影区域的面积为10,则图(b)的阴影面积等于( )
A.40 B.30
C.20 D.10
5.如图11-4-4所示,已知AC⊥BD于点O,△AOD、△AOB、△BOC、△COD 的面积分别为S 、S 、S 、S ,设AC=m,BD=n,则下式中正确的是( ).
6.如图11-4-5 所示,在△ABC 中,E 为BC 的中点,AD⊥BC 于点 D,以下结论:①ADS△ACE; 其中正确的命 题为 .
7.如图11-4-6所示,在△ABC中,AD、BE相交于点O, 若 求:((1)S△BOC :S△AOC : S△AOB|的值.(2)求S△ABC.
8.图11-4-7 所示是某个公园ABCDEF,M为AB 的中点,N 为CD 的中点,P为DE 的中点,Q 为FA 的中点,其中游览区 APEQ 与BNDM 的面积和是900平方米,中间的湖水 AMDP 的面积为361平方米,其余的部分是草地,求草地的总面积.
9.认真阅读,并回答下面问题:
如图11-4-8所示,AD为△ABC的中线,S△ABD与S△ADC相等吗
【解】过 A 点作BC 边上的高h,
∵AD为△ABC的中线
∴BD=DC.
(1)用一句简洁的文字表示上面这段内容的结论: .
(2)利用上面所得的结论,用不同的分割方法分别把下面两个三角形面积4等分(只要割线不同就算一种).
(3)已知:AD为△ABC的中线,点E为AD 边上的中点,若△ABC的面积为20,BD=4,求点E到BC边的距离为多少
能力提升
10.如图11-4-9 所示,三边均不相等的. 若在此三角形内找一点O,使得 的面积均相等.判断下列作法正确的是( ).
A.作中线 AD,再取 AD的中点O
B.分别作中线 AD、BE,再取此两中线的交点O
C.分别作AB、BC的中垂线,再取此两中垂线的交点O
D.分别作 的角平分线,再取此两角平分线的交点O
11.如图11-4-10所示,在正方形 ABCD中,AB=2,∠DCE 是正方形 ABCD 的外角,P 是∠DCE的角平分线CF 上任意一点,则△PBD的面积等于( )
A.1 B.1.5
C.2 D.2.5
12.如图11-4-11 所示,△ABC的面积为 18cm ,点 D、E、F 分别位于 AB、BC、CA上,DE∥AC,且AD=4cm,DB=5cm,则△ABE的面积是( ).
A.8 B.9 C.10 D.12
13.如图11-4-12 所示,在△ABC中,点M是BC 边上任意一点,D、E、F分别是AM、BD、CE 的中点,且S△ABC=1,则 S△DEF=( ).
A B C D
14.如图11-4-13所示,在长方形ABCD中,E 是AD 的中点,F 是CE 的中点.三角形 BDF的面积是6cm ,则长方形ABCD 的面积为 .
15.如图11-4-14所示,面积为16的△ABC中两中线AD⊥BE,若AD:BE=2:3,则 BE 的长为 .
16.探索
在图11-4-15(a)至图 11-4-15(c)中,△ABC的面积为a.
(1)如图(a)所示,延长△ABC的边BC 到点D,使CD=BC,连接DA.若△ACD的面积为S ,则S 「それ (用含 a的代数式表示);
(2)如图(b)所示,延长△ABC的边BC到点D,延长边CA到点 E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S ,则. (用含a的代数式表示),并写出理由;
(3)在图(b)的基础上延长AB到点F,使BF=AB,连接FD、FE,得到△DEF(如图(c)所示).若阴影部分的面积为S ,则S = (用含a的代数式表示).
发现
像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到 (如图(c)所示),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF 的面积是原来△ABC 面积的 倍.
应用
去年在面积为 的 空地上栽种了某种花卉.今年准备扩大种植规模,把 向外进行两次扩展,第一次由 扩展成 第二次由 扩展成 (如图(d)所示).求这两次扩展的区域(即阴影部分)面积共为多少平方米
17.已知,如图11-4-16 所示, ,交 AD的延长线于点E,求证:
18.(1)①问题1:如图11-4-17(a) 所示,已知△ABC,请你过点 A 画一条直线,把 分成面积相等的两部分(在图(a)中画出来,简要写出作法).
②问题2:如图11-4-17(b)所示,已知l ∥l ,点 A、D在l 上,点 B、C 在l 上,试说明△ABO与△DCO 面积相等.
(2)应用:如图 11-4-17(c)所示,在△ABC中,点M在AB 边上,过点 M画一条直线,将△ABC的面积二等分(保留作图痕迹,不写作法).
(3)拓展:如图11-4-17(d)所示,四边形ABCD是一块土地的示意图,过点 D 修一条直路,直路修好后,要保持直路两边的面积相等,请你确定出这条直路(不计直路的占地面积).
①简要写出设计方案,并在图(d)中画出相应的图形.
②说明方案的设计理由.
19.如图11-4-18所示,在△ABC中,AB=AC,AC边上的高BD=10cm.
(1)如图(a)所示,求 AB 边上的高CE 的长.
(2)如图(b)所示,若点 P 为BC 边上任意一点,PM⊥AB于点M,PN⊥AC 于点 N,求 PM+PN的值.
(3)如图(c)所示,若点 P为 BC延长线上任意一点,PM⊥AB 于点 M,PN⊥AC于点 N,在①PM+PN.②PM-PN中有一个是定值,判断出来并求值.
20.阅读理解
如图11-4-19(a)所示,在△ABC中,D是BC的中点.如果用S△ABC表示△ABC的面积,则由等底同高的三角形的面积相等,可得
同理,如图(b)所示,在△ABC 中,D、E 是BC 的三等分点,可得
结论应用
已知:△ABC的面积为1,请利用上面的结论解决下列问题:
(1)如图11-4-20(a)所示,若 D、E 分别是AB、AC 的中点,CD与BE 交于点 F,则△DBF 的面积为 ;
类比推广
(2)如图11-4-20(b)所示,△ABC的面积为1,D、E为AC 的三等分点,F、G为BC 的三等分点,四边形 PECF 的面积.
21.如图11-4-21所示,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C的个数是( ).
A.2 B.3
C.4 D.5
22.如图11-4-22所示,在△ABC中,E是BC上的一点,EC=2BE,点D 是AC 的中点,设△ABC、△ADF、△BEF的面积分别为S△ABC、S△ADF 、SBEF,且S△ABC=12,则S△ADF—S△BEF =( )
A.1 B.2
C.3 D.4
巅峰突破
23.如图11-4-23所示,在矩形ABCD中, E、H、G 在同一条直线上,则阴影部分的面积等于( ).
A.8 B.12
C.16 D.20
24.如图11-4-24 所示,三角形 ABC 内的线段 BD、CE 相交于点 O,已知( OC=2OE,设△BOE、△BOC、△COD 和四边形AEOD 的面积分别为.
(1)求 S : S 的值;
(2)如果 求 S 的值.
直角三角形的三条边长分别为3cm、4cm、5cm,在三角形内部有一点 P,已知点 P 到三角形其中两条边的距离分别为3.2cm和0.5cm,求点 P 到三条边的距离.
基础演练
1. A;2. A; 3. D;4. D; 5. A; 6.①②④.
7.(1)∵BD:CD=3:2,AE:CE=2:1,
∴S△BOC: S△AOC :S△AOB=3:4:6.
(2)∵BD:CD=3:2,S△COD=2,
8.连接AE、AD、BD.
因为 M为AB 的中点,N为CD 的中点,P 为DE 的中点,Q为 FA 的中点,
根据一个三角形的中线平分这个三角形的面积,
所以设S△EFQ=S△AQE=a,S△AEP=S△APD=b,
由题意得:a+b+c+d=900平方米,b+c=361平方米.所以a+d=900-361=539平方米.
即草地的总面积 平方米.
9.(1)三角形中线平分三角形的面积;
(2)如下图所示:
(3)2.5.
能力提升
10. B; 11. C; 12. C
13. D; 14.48cm ; 15.6.
(2)如右图所示,连接AD,
由(1)可知,S△ABC=a.
∵AC=AE,∴S△DEC=2S△ACD=2a.
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
应用:480m
17.连接AC、BE,
∵DC∥AB,∴S△BCD=S△ACD.①
同理:S△BCD=S△BED.②
∵△DCE与△ACD同高,△BED与△ABD同高,
把①,②代入③得:
18.(1)①取 BC中点 D,作直线 AD.
②∵l ∥l ,∴△ABC与△DBC同底等高.
即 S△ABO=S△DCO.
(2)如下图所示,取 BC 中点 D,连接 MD,过点 A 作AN∥MD交BC 于点 N,作直线 MN,则直线MN即为所求.
(3)①如下图所示,连接 DB,过点 A 作 AE//DB交CB的延长线于点E,连接DE,取EC的中点F,连接DF,则 DF即为所求.
②理由:∵AE∥BD,∴S△EBD=S△ABD.
即
∴S△AGD+S四边形GBCD=S△EBG+S四边形GBCD.
∴S△DEC=S四边形ABCD.∵EF=FC,
即S△DFC=S△EDF=S四边形ABFD S四边形ABCD
且AB=AC,∴CE=BD=10cm.
(2)如下图所示,连接AP,过点 B作 BD⊥AC,垂足为 D,
又∵AB=AC,∴PM+PN=BD=10cm.
(3)结论:PM-PN为定值,值为10cm如下图所示,连接AP,
且
又∵AB=AC,∴PM-PN=BD=10cm.
20.
(2)如下图所示,连接CP,设S△PCF=x,S△PCE=y.
则
两式联立可得 即
中考链接
21. C; 22. B
巅峰突破
23. B.
24.(1)根据高相等的三角形的面积之比等于底边之比,
如上图所示,连接OA,设
则
∵S△AOC=2S△AOE,∴x+1+2=2x.
解得.x=3,x+1=4,∴S =3+4=7.
25.如图(a):设AC=4cm,BC=3cm,AB=5cm.
过点 C 作 CD⊥AB 于点 D,连接 PA、PB、PC 过点 P 分别作 PE⊥AC、PF⊥BC、PG⊥AB,如图(b)
∵BC=3<3.2,CD=2.4<3.2
∴点 P 到边 BC的距离是3.2cm.即 PF=3.2cm.
①当PE=0.5cm时,
②当PG=0.5cm时,
显然不成立.
∴点 P 到三条边的距离为3.2cm、0.5cm、0.08cm.
一、课标导航
课标内容 课标要求 目标层次
图形面积 掌握基本图形面积的计算公式 ★
计算面积或利用图形面积解决数学问题
二、核心纲要
1.一些常用图形的面积公式
正方形面积=边长×边长; 长方形(矩形)面积=长×宽; 平行四边形面积=底×高;
三角形面积 底×高; 梯形面积 (上底+下底)×高.
2.计算图形的面积有以下常用方法
(1)和差法:把图形面积用常见图形面积的和或差表示,通过常规图形面积公式计算.
(2)割补法:有时直接求图形面积有困难,我们可以通过分割或补形,把图形转化为容易观察或解决的形状求解.
(3)等积变换法:对某些图形,找出与所求图形面积相等或有关联的特殊图形,通过代换转化易求图形的面积.
(4)等比法:将面积比转化为线段比.
3.在两个三角形中
(1)同(等)高时,面积之比等于底之比.(2)同(等)底时,面积之比等于高之比.
4.等分三角形面积
三角形一边中线平分三角形面积.
5.常见的基本模型
若 AD∥BC,则 S△AOB=S△COD,S△ABC=S△BCD
中小学教育资源及组卷应用平台
平行四边形ABCD
本节重点讲解:图形面积的计算和证明.
三、全能突破
基础演练
1.如图11-4-1所示,在△ABC 中,点 D、E、F 分别为BC、AD、AC 的中点,且S△ABc=16,则.S△DEFI的面积为( ).
A.2 B.8
C.4 D.1
2.如图11-4-2 所示,在△ABC 中,AB=1,BC=2,则△ABC 的高AD:CE为( )
A.1:2 B.2: 1
C.1:4 D.4: 1
3.已知△ABC的面积为3,边 BC长为2,以点B 为原点,BC所在的直线为x轴建立平面直角坐标系,则点 A的纵坐标为( )
A.3 B. -3
C.6 D.±3
4.图11-4-3(a)、(b)为两个相同的矩形,若图(a)阴影区域的面积为10,则图(b)的阴影面积等于( )
A.40 B.30
C.20 D.10
5.如图11-4-4所示,已知AC⊥BD于点O,△AOD、△AOB、△BOC、△COD 的面积分别为S 、S 、S 、S ,设AC=m,BD=n,则下式中正确的是( ).
6.如图11-4-5 所示,在△ABC 中,E 为BC 的中点,AD⊥BC 于点 D,以下结论:①AD
7.如图11-4-6所示,在△ABC中,AD、BE相交于点O, 若 求:((1)S△BOC :S△AOC : S△AOB|的值.(2)求S△ABC.
8.图11-4-7 所示是某个公园ABCDEF,M为AB 的中点,N 为CD 的中点,P为DE 的中点,Q 为FA 的中点,其中游览区 APEQ 与BNDM 的面积和是900平方米,中间的湖水 AMDP 的面积为361平方米,其余的部分是草地,求草地的总面积.
9.认真阅读,并回答下面问题:
如图11-4-8所示,AD为△ABC的中线,S△ABD与S△ADC相等吗
【解】过 A 点作BC 边上的高h,
∵AD为△ABC的中线
∴BD=DC.
(1)用一句简洁的文字表示上面这段内容的结论: .
(2)利用上面所得的结论,用不同的分割方法分别把下面两个三角形面积4等分(只要割线不同就算一种).
(3)已知:AD为△ABC的中线,点E为AD 边上的中点,若△ABC的面积为20,BD=4,求点E到BC边的距离为多少
能力提升
10.如图11-4-9 所示,三边均不相等的. 若在此三角形内找一点O,使得 的面积均相等.判断下列作法正确的是( ).
A.作中线 AD,再取 AD的中点O
B.分别作中线 AD、BE,再取此两中线的交点O
C.分别作AB、BC的中垂线,再取此两中垂线的交点O
D.分别作 的角平分线,再取此两角平分线的交点O
11.如图11-4-10所示,在正方形 ABCD中,AB=2,∠DCE 是正方形 ABCD 的外角,P 是∠DCE的角平分线CF 上任意一点,则△PBD的面积等于( )
A.1 B.1.5
C.2 D.2.5
12.如图11-4-11 所示,△ABC的面积为 18cm ,点 D、E、F 分别位于 AB、BC、CA上,DE∥AC,且AD=4cm,DB=5cm,则△ABE的面积是( ).
A.8 B.9 C.10 D.12
13.如图11-4-12 所示,在△ABC中,点M是BC 边上任意一点,D、E、F分别是AM、BD、CE 的中点,且S△ABC=1,则 S△DEF=( ).
A B C D
14.如图11-4-13所示,在长方形ABCD中,E 是AD 的中点,F 是CE 的中点.三角形 BDF的面积是6cm ,则长方形ABCD 的面积为 .
15.如图11-4-14所示,面积为16的△ABC中两中线AD⊥BE,若AD:BE=2:3,则 BE 的长为 .
16.探索
在图11-4-15(a)至图 11-4-15(c)中,△ABC的面积为a.
(1)如图(a)所示,延长△ABC的边BC 到点D,使CD=BC,连接DA.若△ACD的面积为S ,则S 「それ (用含 a的代数式表示);
(2)如图(b)所示,延长△ABC的边BC到点D,延长边CA到点 E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S ,则. (用含a的代数式表示),并写出理由;
(3)在图(b)的基础上延长AB到点F,使BF=AB,连接FD、FE,得到△DEF(如图(c)所示).若阴影部分的面积为S ,则S = (用含a的代数式表示).
发现
像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到 (如图(c)所示),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF 的面积是原来△ABC 面积的 倍.
应用
去年在面积为 的 空地上栽种了某种花卉.今年准备扩大种植规模,把 向外进行两次扩展,第一次由 扩展成 第二次由 扩展成 (如图(d)所示).求这两次扩展的区域(即阴影部分)面积共为多少平方米
17.已知,如图11-4-16 所示, ,交 AD的延长线于点E,求证:
18.(1)①问题1:如图11-4-17(a) 所示,已知△ABC,请你过点 A 画一条直线,把 分成面积相等的两部分(在图(a)中画出来,简要写出作法).
②问题2:如图11-4-17(b)所示,已知l ∥l ,点 A、D在l 上,点 B、C 在l 上,试说明△ABO与△DCO 面积相等.
(2)应用:如图 11-4-17(c)所示,在△ABC中,点M在AB 边上,过点 M画一条直线,将△ABC的面积二等分(保留作图痕迹,不写作法).
(3)拓展:如图11-4-17(d)所示,四边形ABCD是一块土地的示意图,过点 D 修一条直路,直路修好后,要保持直路两边的面积相等,请你确定出这条直路(不计直路的占地面积).
①简要写出设计方案,并在图(d)中画出相应的图形.
②说明方案的设计理由.
19.如图11-4-18所示,在△ABC中,AB=AC,AC边上的高BD=10cm.
(1)如图(a)所示,求 AB 边上的高CE 的长.
(2)如图(b)所示,若点 P 为BC 边上任意一点,PM⊥AB于点M,PN⊥AC 于点 N,求 PM+PN的值.
(3)如图(c)所示,若点 P为 BC延长线上任意一点,PM⊥AB 于点 M,PN⊥AC于点 N,在①PM+PN.②PM-PN中有一个是定值,判断出来并求值.
20.阅读理解
如图11-4-19(a)所示,在△ABC中,D是BC的中点.如果用S△ABC表示△ABC的面积,则由等底同高的三角形的面积相等,可得
同理,如图(b)所示,在△ABC 中,D、E 是BC 的三等分点,可得
结论应用
已知:△ABC的面积为1,请利用上面的结论解决下列问题:
(1)如图11-4-20(a)所示,若 D、E 分别是AB、AC 的中点,CD与BE 交于点 F,则△DBF 的面积为 ;
类比推广
(2)如图11-4-20(b)所示,△ABC的面积为1,D、E为AC 的三等分点,F、G为BC 的三等分点,四边形 PECF 的面积.
21.如图11-4-21所示,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C的个数是( ).
A.2 B.3
C.4 D.5
22.如图11-4-22所示,在△ABC中,E是BC上的一点,EC=2BE,点D 是AC 的中点,设△ABC、△ADF、△BEF的面积分别为S△ABC、S△ADF 、SBEF,且S△ABC=12,则S△ADF—S△BEF =( )
A.1 B.2
C.3 D.4
巅峰突破
23.如图11-4-23所示,在矩形ABCD中, E、H、G 在同一条直线上,则阴影部分的面积等于( ).
A.8 B.12
C.16 D.20
24.如图11-4-24 所示,三角形 ABC 内的线段 BD、CE 相交于点 O,已知( OC=2OE,设△BOE、△BOC、△COD 和四边形AEOD 的面积分别为.
(1)求 S : S 的值;
(2)如果 求 S 的值.
直角三角形的三条边长分别为3cm、4cm、5cm,在三角形内部有一点 P,已知点 P 到三角形其中两条边的距离分别为3.2cm和0.5cm,求点 P 到三条边的距离.
基础演练
1. A;2. A; 3. D;4. D; 5. A; 6.①②④.
7.(1)∵BD:CD=3:2,AE:CE=2:1,
∴S△BOC: S△AOC :S△AOB=3:4:6.
(2)∵BD:CD=3:2,S△COD=2,
8.连接AE、AD、BD.
因为 M为AB 的中点,N为CD 的中点,P 为DE 的中点,Q为 FA 的中点,
根据一个三角形的中线平分这个三角形的面积,
所以设S△EFQ=S△AQE=a,S△AEP=S△APD=b,
由题意得:a+b+c+d=900平方米,b+c=361平方米.所以a+d=900-361=539平方米.
即草地的总面积 平方米.
9.(1)三角形中线平分三角形的面积;
(2)如下图所示:
(3)2.5.
能力提升
10. B; 11. C; 12. C
13. D; 14.48cm ; 15.6.
(2)如右图所示,连接AD,
由(1)可知,S△ABC=a.
∵AC=AE,∴S△DEC=2S△ACD=2a.
∴扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
应用:480m
17.连接AC、BE,
∵DC∥AB,∴S△BCD=S△ACD.①
同理:S△BCD=S△BED.②
∵△DCE与△ACD同高,△BED与△ABD同高,
把①,②代入③得:
18.(1)①取 BC中点 D,作直线 AD.
②∵l ∥l ,∴△ABC与△DBC同底等高.
即 S△ABO=S△DCO.
(2)如下图所示,取 BC 中点 D,连接 MD,过点 A 作AN∥MD交BC 于点 N,作直线 MN,则直线MN即为所求.
(3)①如下图所示,连接 DB,过点 A 作 AE//DB交CB的延长线于点E,连接DE,取EC的中点F,连接DF,则 DF即为所求.
②理由:∵AE∥BD,∴S△EBD=S△ABD.
即
∴S△AGD+S四边形GBCD=S△EBG+S四边形GBCD.
∴S△DEC=S四边形ABCD.∵EF=FC,
即S△DFC=S△EDF=S四边形ABFD S四边形ABCD
且AB=AC,∴CE=BD=10cm.
(2)如下图所示,连接AP,过点 B作 BD⊥AC,垂足为 D,
又∵AB=AC,∴PM+PN=BD=10cm.
(3)结论:PM-PN为定值,值为10cm如下图所示,连接AP,
且
又∵AB=AC,∴PM-PN=BD=10cm.
20.
(2)如下图所示,连接CP,设S△PCF=x,S△PCE=y.
则
两式联立可得 即
中考链接
21. C; 22. B
巅峰突破
23. B.
24.(1)根据高相等的三角形的面积之比等于底边之比,
如上图所示,连接OA,设
则
∵S△AOC=2S△AOE,∴x+1+2=2x.
解得.x=3,x+1=4,∴S =3+4=7.
25.如图(a):设AC=4cm,BC=3cm,AB=5cm.
过点 C 作 CD⊥AB 于点 D,连接 PA、PB、PC 过点 P 分别作 PE⊥AC、PF⊥BC、PG⊥AB,如图(b)
∵BC=3<3.2,CD=2.4<3.2
∴点 P 到边 BC的距离是3.2cm.即 PF=3.2cm.
①当PE=0.5cm时,
②当PG=0.5cm时,
显然不成立.
∴点 P 到三条边的距离为3.2cm、0.5cm、0.08cm.
