11.3 多边形及其内角和 培优训练(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 11.3 多边形及其内角和 培优训练(含答案)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 646.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 07:06:54 | ||
图片预览



文档简介
11.3 多边形及其内角和
一、课标导航
课标内容 课标要求 目标层次
多边形 理解多边形及正多边形的概念.掌握多边形的内角和及其外角和的计算公式 ★
会用多边形的内角和与外角和公式解决计算问题 ★★
镶嵌 知道用任意一个三角形、四边形或正六边形可以镶嵌 ★
能用正三角形、正方形、正六边形进行简单的镶嵌设计
二、核心纲要
1.多边形的有关概念
(1)多边形:在平面内,由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形.
(2)多边形的内角和外角:多边形相邻的两边组成的角叫做多边形的内角;多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
(3)多边形的对角线:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
(4)正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
(5)凸、凹多边形:画出多边形的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的图形叫做凸多边形,否则称为凹多边形.
注:没有特殊说明的情况下,我们所说的多边形都是凸多边形.
2.多边形的内角和
n边形的内角和公式:(n-2)·180°.
3.多边形的外角和
n边形的外角和等于 360°.
注:多边形的外角和与边数无关.
4.多边形的对角线的条数
多边形的对角线的条数为:
5.镶嵌
(1)定义:用形状相同或不同的封闭的平面图形进行拼接,彼此之间不留空隙,不重叠地拼接在一起,这类问题叫做平面镶嵌.
(2)镶嵌的条件:拼在同一顶点的几个多边形的内角和恰好为360°.
注:①用同一种多边形进行镶嵌的图形有:三角形、四边形、正六边形.(其中三角形和四边形是任意的)
②用两种正多边形进行镶嵌的图形常用的有:常用的有正三角形和正四边形;正三角形和正六边形;正四边形和正八边形;还有正三角形和正十二边形;正五边形和正十边形.
中小学教育资源及组卷应用平台
本节重点讲解:一个条件(镶嵌的条件),两个概念(多边形的有关概念和镶嵌),两个定理(多边形的内角和及外角和定理).
三、全能突破
基础演练
1.如果一个多边形的内角和等于它的外角和的两倍,则这个多边形是( ).
A.四边形 B.五边形 C.六边形 D.七边形
2.某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°”;乙说:“多边形的边数每增加1,则外角和增加 180°”;丙说:“多边形的内角和不小于其外角和”;丁说:“只要是多边形,外角和都是360°”.你认为正确的是( )
A.甲和丁 B.乙和丙 C.丙和丁 D.以上都不对
3.小华家装修房屋,用同边长的几种不同的正多边形砖铺地,顶点连着顶点,为铺满地面而不重叠,瓷砖的形状可能有( )
A.正三角形、正六边形 B.正三角形、正五边形、正八边形
C.正六边形、正五边形 D.正八边形、正三角形
4.如图11-3-1所示,在锐角△ABC中,BD、CE 分别是AC、AB边上的高,且BD,CE 交于点F,若∠A=52°,则∠BFC的度数是( ).
A.108° B.128° C.138° D.158°
5.如图11-3-2所示,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为( ).
A.π/2 B.π/3 C.π/4 D.2π
6.如图11-3-3所示,小林从 P 点向西直走 12 米后,向左转,转动的角度为α,再走 12米,如此重复,小林共走了 108米回到点 P,则α= .
7.如图11-3-4所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
8.(1)已知,∠AOB=65°,P是平面上的任意一点,过点 P作PE⊥OA,PF⊥OB,垂足分别为点 E、F,求∠EPF 的度数.
(2)探究∠EPF 与∠AOB有什么关系 (直接写出结论)
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系
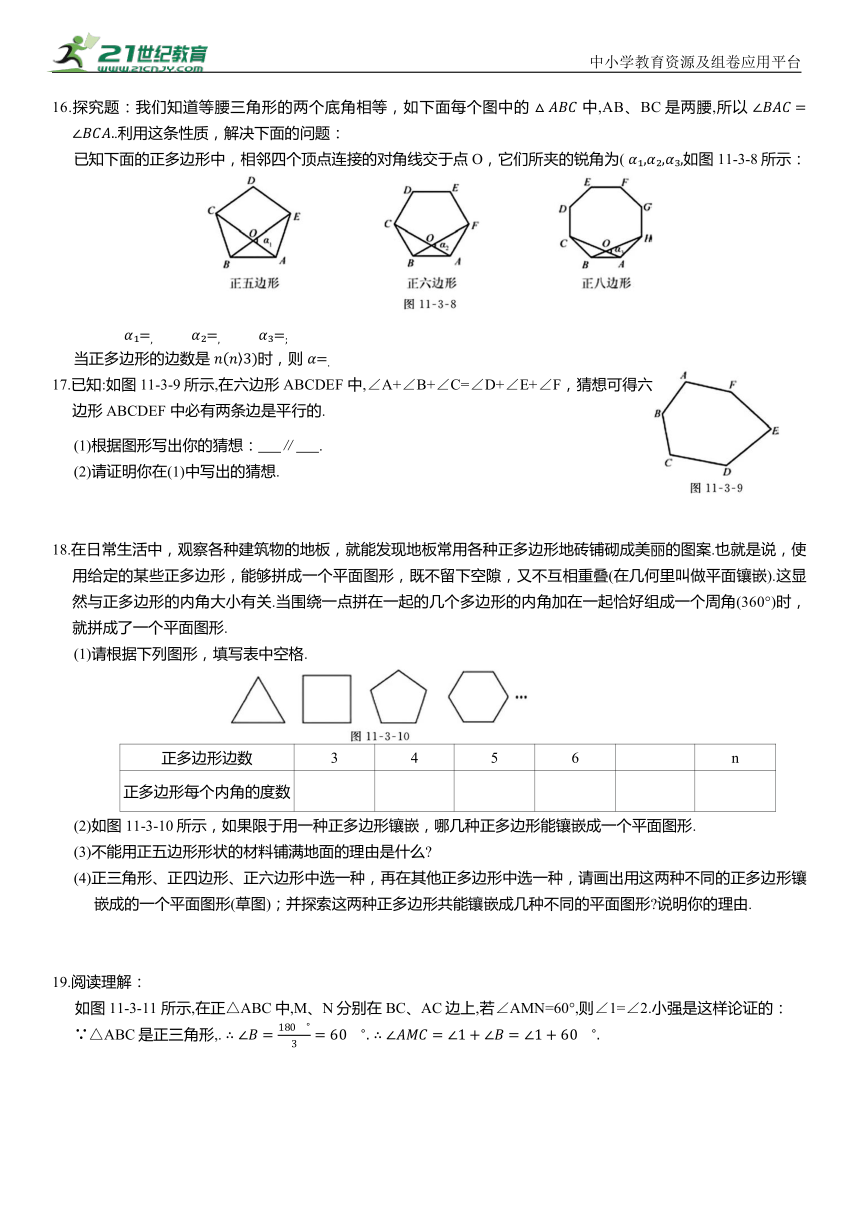
16.探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的 中,AB、BC是两腰,所以 .利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O,它们所夹的锐角为( 如图11-3-8所示:
当正多边形的边数是 时,则
17.已知:如图11-3-9所示,在六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可得六边形ABCDEF 中必有两条边是平行的.
(1)根据图形写出你的猜想: ∥ .
(2)请证明你在(1)中写出的猜想.
18.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请根据下列图形,填写表中空格.
正多边形边数 3 4 5 6 n
正多边形每个内角的度数
(2)如图11-3-10所示,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形.
(3)不能用正五边形形状的材料铺满地面的理由是什么
(4)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形 说明你的理由.
19.阅读理解:
如图11-3-11 所示,在正△ABC中,M、N分别在BC、AC边上,若∠AMN=60°,则∠1=∠2.小强是这样论证的:
∵△ABC是正三角形,.
又∠AMC=∠2+∠AMN,∠AMN=60°,∴∠AMC=∠2+60°.∴∠1=∠2.
(1)类比应用:如图11-3-12所示,将阅读理解中的正三角形换成正四边形 ABCD,M、N分别为BC、CD 上的点,类似地:若 则 .请你用小强的证明方法论证.
(2)拓展延伸:请你将上述命题推广到一般,如图11-3-13所示,ABCDEF…是正n边形.
写出命题: .
20.如图11-3-14 所示,在四边形 ABCD 中,∠ABC的角平分线及外角∠DCE的平分线所在的直线相交于点F,若∠A=α,∠D=β;
(1)如图(a)所示,α+β>180°,试用α,β表示∠F,直接写出结论;
(2)如图(b)所示,α+β<180°,请在图(b)中画出∠F,并试用α,β表示∠F;
(3)一定存在∠F 吗 如有,写出∠F 的值,如不一定,直接写出α,β满足什么条件时,不存在∠F.
21.正十边形的每个外角等于( ).
A.18° B.36° C.45° D.60°
22.已知一个多边形的内角和是外角和 ,则这个多边形是
23.用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图11-3-15(a)所示,用n个全等的正六边形按这种方式拼接,如图11-3-15(b)所示,若围成一圈后中间也形成一个正多边形,则n的值为 .
巅峰突破
24.凸n边形中有且仅有两个内角为钝角,则n的最大值是( ).
A.4 B.5 C.6 D.7
25.在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的 边数是 .
26.如图11-3-16所示,六边形 ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11,FA-CD=3,求BC+DE的值.
基础演练
C; 2. A; 3. A; 4. B; 5. D; 6.40°
7.∵∠EHC是△GHC的一个外角,
∴∠EHC=∠CGH+∠C.
同理可证:∠CGH=∠D+∠E.
∴∠EHC=∠E+∠D+∠C.
∵∠EHC=∠BHF,∠A+∠B+∠BHF+∠F=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
8.(1)①若点 P 在∠AOB的内部,如图(a)所示四边形OEPF中,∠AOB=65°,
∵PE⊥OA,PF⊥OB,
∴∠OEP+∠PFO=180°.
∠AOB+∠OEP+∠EPF+∠PFO=360°,
②若点 P 在∠AOB的外部,如图(b)所示
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠PFO=90°.
又∵∠1=∠2,∴∠EPF=∠AOB=65°.
(2)∠EPF+∠AOB=180°或∠EPF=∠AOB.
(3)如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补.
9.(1)结论:AE∥FC.如图(c)所示,
∵∠B=∠D=90°,∴∠BAD+∠BCD=180°.
又∵AE、CF分别是∠BAD、∠DCB的角平分线,
∵∠1+∠5=90°,∴∠3=∠5,∴AE∥FC.
(2)结论:AE∥CF.
(3)结论:AE⊥CF.如图(d)所示,CF 与AE 相交于点 M,
又∵∠B=∠D=90°,
∴∠BAD+∠DCB=180°,
∵∠DCB+∠BCE=180°,
∴∠BAD=∠BCE,
∵AE、CF 分别是∠BAD和∠BCE的角平分线,
∵∠3=∠4,∴∠CMA=∠B=90°.∴AE⊥CF.
能力提升
10. C; 11C. 12.900°. 13.125.
14.(1)18;130°.(2)10、11、12.(3)4 或5.
15.72°或144°.
16.72°,60°,45° .(提示:可从外角考虑
17.(1)猜想:AF∥CD;
(2)证法一:如下左图所示,连接AD.
∵在六边形ABCDEF中,
∠BAF+∠B+∠C+∠CDE+∠E+∠F
∠BAF+∠B+∠C=∠CDE+∠E+∠F,
即∠1+∠2+∠B+∠C=360°.
∵在四边形ABCD中,∠1+∠B+∠C+∠3=360°,
∴∠2=∠3.∴AF∥CD.
证法二:如上右图所示,连接AC.证明过程略.
18.(1)60°,90°,108°,120°,…,(n—2)n·180°;
(2)正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形.
(3)因为正五边形的每一个内角是 108°,它不是 360°的约数.所以不能.
(4)如:正方形和正八边形(如下图所示),设在一个顶点周围有m个正方形的角,n个正八边形的角,那么m,n应是方程m·90+n·135=360的正整数解.即2m+3n=8的正整数解,只有 组,∴符合条件的图形只有一种.
理由:∵四边形 ABCD是正四边形,
∴∠AMC=∠1+∠B=∠1+90°.
又∠AMC=∠2+∠AMN,∠AMN=90°,
∴∠AMC=∠2+90°,∴∠1=∠2.
(2)已知,正n边形ABCDEF…中,M、N分别为BC、CD上的点,若 则∠1=∠2.
(2)如下图所示,
,且∠A=α,
∠D=β,
∵BG平分∠ABC,CH平分∠DCE,
∴∠ABC=2∠GBC,∠DCE=2∠ECH.
∵∠GBC是△BCF 的一个外角,
∴∠GBC=∠F+∠BCF.
∴2∠GBC=2∠F+2∠BCF.
∵∠BCF=∠ECH,
∴2∠GBC=2∠F+2∠ECH.
∴∠ABC=2∠F+∠DCE.
∵∠DCE+∠DCB=180°,
(3)α+β=180°时,不存在∠F.
中考链接
21. B; 22.五; 23.6
巅峰突破
24. B
25.14或15.
26.如下图所示,将六边形 ABCDEF的三边AB,CD,EF双向延长,得△HGM.
∵六边形内角和是720°,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°.
∴该六边形各外角均为60°.
∴△AFH、△GBC、△DME、△HGM均为等边三角形.
∴BC+DE=GC+DM=GM-CD=HG-CD=AH+AB+GB-CD=AB+BC+FA-CD=11+3=14.
一、课标导航
课标内容 课标要求 目标层次
多边形 理解多边形及正多边形的概念.掌握多边形的内角和及其外角和的计算公式 ★
会用多边形的内角和与外角和公式解决计算问题 ★★
镶嵌 知道用任意一个三角形、四边形或正六边形可以镶嵌 ★
能用正三角形、正方形、正六边形进行简单的镶嵌设计
二、核心纲要
1.多边形的有关概念
(1)多边形:在平面内,由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形.
(2)多边形的内角和外角:多边形相邻的两边组成的角叫做多边形的内角;多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
(3)多边形的对角线:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
(4)正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
(5)凸、凹多边形:画出多边形的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的图形叫做凸多边形,否则称为凹多边形.
注:没有特殊说明的情况下,我们所说的多边形都是凸多边形.
2.多边形的内角和
n边形的内角和公式:(n-2)·180°.
3.多边形的外角和
n边形的外角和等于 360°.
注:多边形的外角和与边数无关.
4.多边形的对角线的条数
多边形的对角线的条数为:
5.镶嵌
(1)定义:用形状相同或不同的封闭的平面图形进行拼接,彼此之间不留空隙,不重叠地拼接在一起,这类问题叫做平面镶嵌.
(2)镶嵌的条件:拼在同一顶点的几个多边形的内角和恰好为360°.
注:①用同一种多边形进行镶嵌的图形有:三角形、四边形、正六边形.(其中三角形和四边形是任意的)
②用两种正多边形进行镶嵌的图形常用的有:常用的有正三角形和正四边形;正三角形和正六边形;正四边形和正八边形;还有正三角形和正十二边形;正五边形和正十边形.
中小学教育资源及组卷应用平台
本节重点讲解:一个条件(镶嵌的条件),两个概念(多边形的有关概念和镶嵌),两个定理(多边形的内角和及外角和定理).
三、全能突破
基础演练
1.如果一个多边形的内角和等于它的外角和的两倍,则这个多边形是( ).
A.四边形 B.五边形 C.六边形 D.七边形
2.某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°”;乙说:“多边形的边数每增加1,则外角和增加 180°”;丙说:“多边形的内角和不小于其外角和”;丁说:“只要是多边形,外角和都是360°”.你认为正确的是( )
A.甲和丁 B.乙和丙 C.丙和丁 D.以上都不对
3.小华家装修房屋,用同边长的几种不同的正多边形砖铺地,顶点连着顶点,为铺满地面而不重叠,瓷砖的形状可能有( )
A.正三角形、正六边形 B.正三角形、正五边形、正八边形
C.正六边形、正五边形 D.正八边形、正三角形
4.如图11-3-1所示,在锐角△ABC中,BD、CE 分别是AC、AB边上的高,且BD,CE 交于点F,若∠A=52°,则∠BFC的度数是( ).
A.108° B.128° C.138° D.158°
5.如图11-3-2所示,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为( ).
A.π/2 B.π/3 C.π/4 D.2π
6.如图11-3-3所示,小林从 P 点向西直走 12 米后,向左转,转动的角度为α,再走 12米,如此重复,小林共走了 108米回到点 P,则α= .
7.如图11-3-4所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
8.(1)已知,∠AOB=65°,P是平面上的任意一点,过点 P作PE⊥OA,PF⊥OB,垂足分别为点 E、F,求∠EPF 的度数.
(2)探究∠EPF 与∠AOB有什么关系 (直接写出结论)
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系
16.探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的 中,AB、BC是两腰,所以 .利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O,它们所夹的锐角为( 如图11-3-8所示:
当正多边形的边数是 时,则
17.已知:如图11-3-9所示,在六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可得六边形ABCDEF 中必有两条边是平行的.
(1)根据图形写出你的猜想: ∥ .
(2)请证明你在(1)中写出的猜想.
18.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请根据下列图形,填写表中空格.
正多边形边数 3 4 5 6 n
正多边形每个内角的度数
(2)如图11-3-10所示,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形.
(3)不能用正五边形形状的材料铺满地面的理由是什么
(4)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形 说明你的理由.
19.阅读理解:
如图11-3-11 所示,在正△ABC中,M、N分别在BC、AC边上,若∠AMN=60°,则∠1=∠2.小强是这样论证的:
∵△ABC是正三角形,.
又∠AMC=∠2+∠AMN,∠AMN=60°,∴∠AMC=∠2+60°.∴∠1=∠2.
(1)类比应用:如图11-3-12所示,将阅读理解中的正三角形换成正四边形 ABCD,M、N分别为BC、CD 上的点,类似地:若 则 .请你用小强的证明方法论证.
(2)拓展延伸:请你将上述命题推广到一般,如图11-3-13所示,ABCDEF…是正n边形.
写出命题: .
20.如图11-3-14 所示,在四边形 ABCD 中,∠ABC的角平分线及外角∠DCE的平分线所在的直线相交于点F,若∠A=α,∠D=β;
(1)如图(a)所示,α+β>180°,试用α,β表示∠F,直接写出结论;
(2)如图(b)所示,α+β<180°,请在图(b)中画出∠F,并试用α,β表示∠F;
(3)一定存在∠F 吗 如有,写出∠F 的值,如不一定,直接写出α,β满足什么条件时,不存在∠F.
21.正十边形的每个外角等于( ).
A.18° B.36° C.45° D.60°
22.已知一个多边形的内角和是外角和 ,则这个多边形是
23.用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图11-3-15(a)所示,用n个全等的正六边形按这种方式拼接,如图11-3-15(b)所示,若围成一圈后中间也形成一个正多边形,则n的值为 .
巅峰突破
24.凸n边形中有且仅有两个内角为钝角,则n的最大值是( ).
A.4 B.5 C.6 D.7
25.在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的 边数是 .
26.如图11-3-16所示,六边形 ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11,FA-CD=3,求BC+DE的值.
基础演练
C; 2. A; 3. A; 4. B; 5. D; 6.40°
7.∵∠EHC是△GHC的一个外角,
∴∠EHC=∠CGH+∠C.
同理可证:∠CGH=∠D+∠E.
∴∠EHC=∠E+∠D+∠C.
∵∠EHC=∠BHF,∠A+∠B+∠BHF+∠F=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
8.(1)①若点 P 在∠AOB的内部,如图(a)所示四边形OEPF中,∠AOB=65°,
∵PE⊥OA,PF⊥OB,
∴∠OEP+∠PFO=180°.
∠AOB+∠OEP+∠EPF+∠PFO=360°,
②若点 P 在∠AOB的外部,如图(b)所示
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠PFO=90°.
又∵∠1=∠2,∴∠EPF=∠AOB=65°.
(2)∠EPF+∠AOB=180°或∠EPF=∠AOB.
(3)如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补.
9.(1)结论:AE∥FC.如图(c)所示,
∵∠B=∠D=90°,∴∠BAD+∠BCD=180°.
又∵AE、CF分别是∠BAD、∠DCB的角平分线,
∵∠1+∠5=90°,∴∠3=∠5,∴AE∥FC.
(2)结论:AE∥CF.
(3)结论:AE⊥CF.如图(d)所示,CF 与AE 相交于点 M,
又∵∠B=∠D=90°,
∴∠BAD+∠DCB=180°,
∵∠DCB+∠BCE=180°,
∴∠BAD=∠BCE,
∵AE、CF 分别是∠BAD和∠BCE的角平分线,
∵∠3=∠4,∴∠CMA=∠B=90°.∴AE⊥CF.
能力提升
10. C; 11C. 12.900°. 13.125.
14.(1)18;130°.(2)10、11、12.(3)4 或5.
15.72°或144°.
16.72°,60°,45° .(提示:可从外角考虑
17.(1)猜想:AF∥CD;
(2)证法一:如下左图所示,连接AD.
∵在六边形ABCDEF中,
∠BAF+∠B+∠C+∠CDE+∠E+∠F
∠BAF+∠B+∠C=∠CDE+∠E+∠F,
即∠1+∠2+∠B+∠C=360°.
∵在四边形ABCD中,∠1+∠B+∠C+∠3=360°,
∴∠2=∠3.∴AF∥CD.
证法二:如上右图所示,连接AC.证明过程略.
18.(1)60°,90°,108°,120°,…,(n—2)n·180°;
(2)正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形.
(3)因为正五边形的每一个内角是 108°,它不是 360°的约数.所以不能.
(4)如:正方形和正八边形(如下图所示),设在一个顶点周围有m个正方形的角,n个正八边形的角,那么m,n应是方程m·90+n·135=360的正整数解.即2m+3n=8的正整数解,只有 组,∴符合条件的图形只有一种.
理由:∵四边形 ABCD是正四边形,
∴∠AMC=∠1+∠B=∠1+90°.
又∠AMC=∠2+∠AMN,∠AMN=90°,
∴∠AMC=∠2+90°,∴∠1=∠2.
(2)已知,正n边形ABCDEF…中,M、N分别为BC、CD上的点,若 则∠1=∠2.
(2)如下图所示,
,且∠A=α,
∠D=β,
∵BG平分∠ABC,CH平分∠DCE,
∴∠ABC=2∠GBC,∠DCE=2∠ECH.
∵∠GBC是△BCF 的一个外角,
∴∠GBC=∠F+∠BCF.
∴2∠GBC=2∠F+2∠BCF.
∵∠BCF=∠ECH,
∴2∠GBC=2∠F+2∠ECH.
∴∠ABC=2∠F+∠DCE.
∵∠DCE+∠DCB=180°,
(3)α+β=180°时,不存在∠F.
中考链接
21. B; 22.五; 23.6
巅峰突破
24. B
25.14或15.
26.如下图所示,将六边形 ABCDEF的三边AB,CD,EF双向延长,得△HGM.
∵六边形内角和是720°,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°.
∴该六边形各外角均为60°.
∴△AFH、△GBC、△DME、△HGM均为等边三角形.
∴BC+DE=GC+DM=GM-CD=HG-CD=AH+AB+GB-CD=AB+BC+FA-CD=11+3=14.
