全等的构造——巧添辅助线 培优训练(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 全等的构造——巧添辅助线 培优训练(含答案)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 07:10:19 | ||
图片预览


文档简介
全等的构造——巧添辅助线
一、课标导航
课标内容 课标要求 目标层次
全等的构造 全等三角形的常见辅助线的添加方法 ★
掌握全等三角形的辅助线的添加方法,并提高解决实际问题的能力
二、核心纲要
1.添加辅助线的方法和语言表述
(1)作线段:连接…….
(2)作平行线:过点……作……//……
(3)作垂线(作高):过点……作……⊥……,垂足为…
(4)作中线:取……中点……,连接…….
(5)延长并截取线段:延长……使……等于…
(6)截取等长线段:在······上截取······,使······等于······.
(7)作角平分线:作……平分……作角……等于已知角……
(8)作一个角等于已知角:作角……等于……
2.全等三角形中的基本图形的构造与运用
常用的辅助线的添加方法:
(1)倍长中线(或类中线)法:若遇到三角形的中线或类中线(与中点有关的线段),通常考虑倍长中线或类中线(与中点有关的线段),构造全等三角形.
(2)截长补短法:若遇到证明线段的和、差、倍、分关系时,通常考虑截长补短法,构造全等三角形.
①截长:在较长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;
②补短:将一条较短线段延长,延长部分等于另一条较短线段,然后证明新线段等于较长线段;或延长一条较短线段等于较长线段,然后证明延长部分等于另一条较短线段.
(3)有的题目需要根据几何图形的特殊性或题目中的条件和结论考虑添加辅助线.
3.基本模型
中小学教育资源及组卷应用平台
本节重点讲解:辅助线的作法及应用.
三、全能突破
基础演练
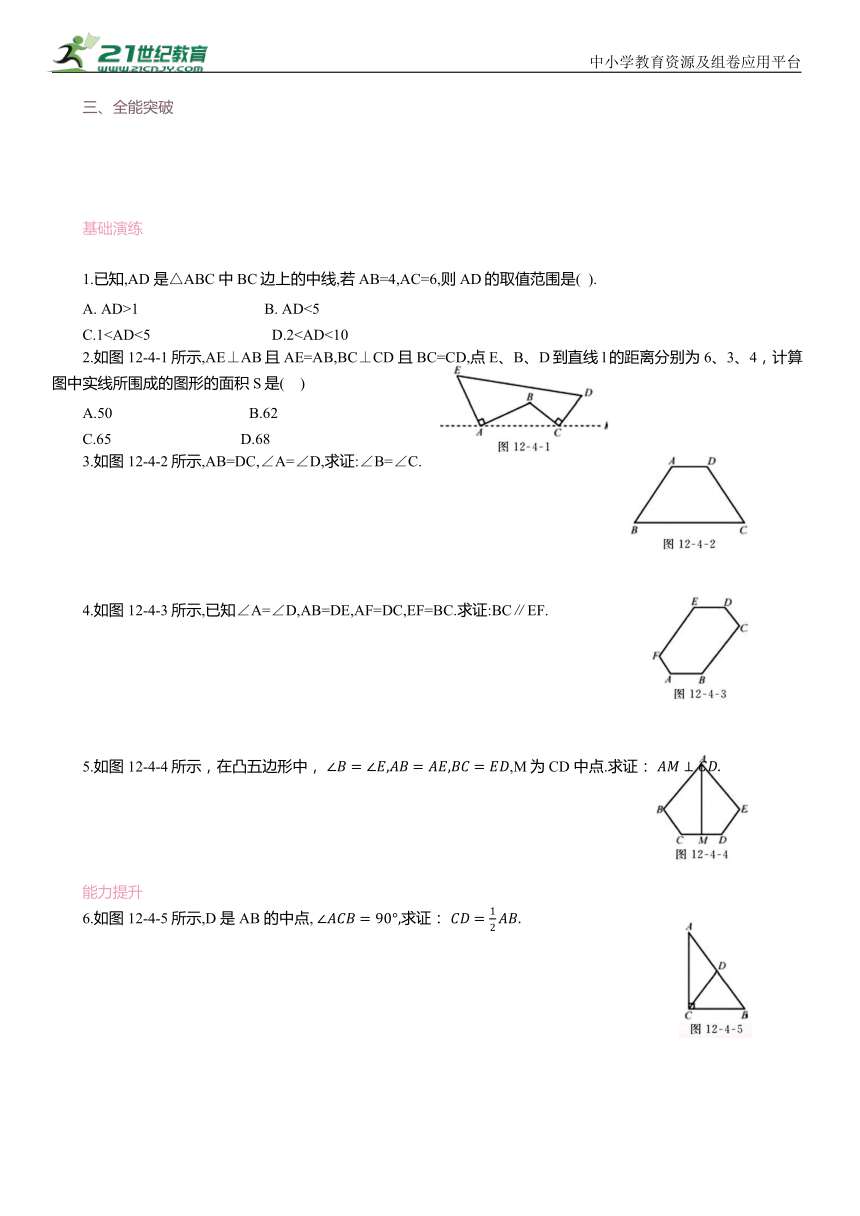
1.已知,AD 是△ABC中BC边上的中线,若AB=4,AC=6,则AD的取值范围是( ).
A. AD>1 B. AD<5
C.12.如图12-4-1所示,AE⊥AB且AE=AB,BC⊥CD 且BC=CD,点E、B、D到直线l的距离分别为6、3、4,计算图中实线所围成的图形的面积S是( )
A.50 B.62
C.65 D.68
3.如图12-4-2所示,AB=DC,∠A=∠D,求证:∠B=∠C.
4.如图12-4-3所示,已知∠A=∠D,AB=DE,AF=DC,EF=BC.求证:BC∥EF.
5.如图12-4-4所示,在凸五边形中, ,M为CD 中点.求证:
能力提升
6.如图12-4-5所示,D 是AB 的中点, 求证:
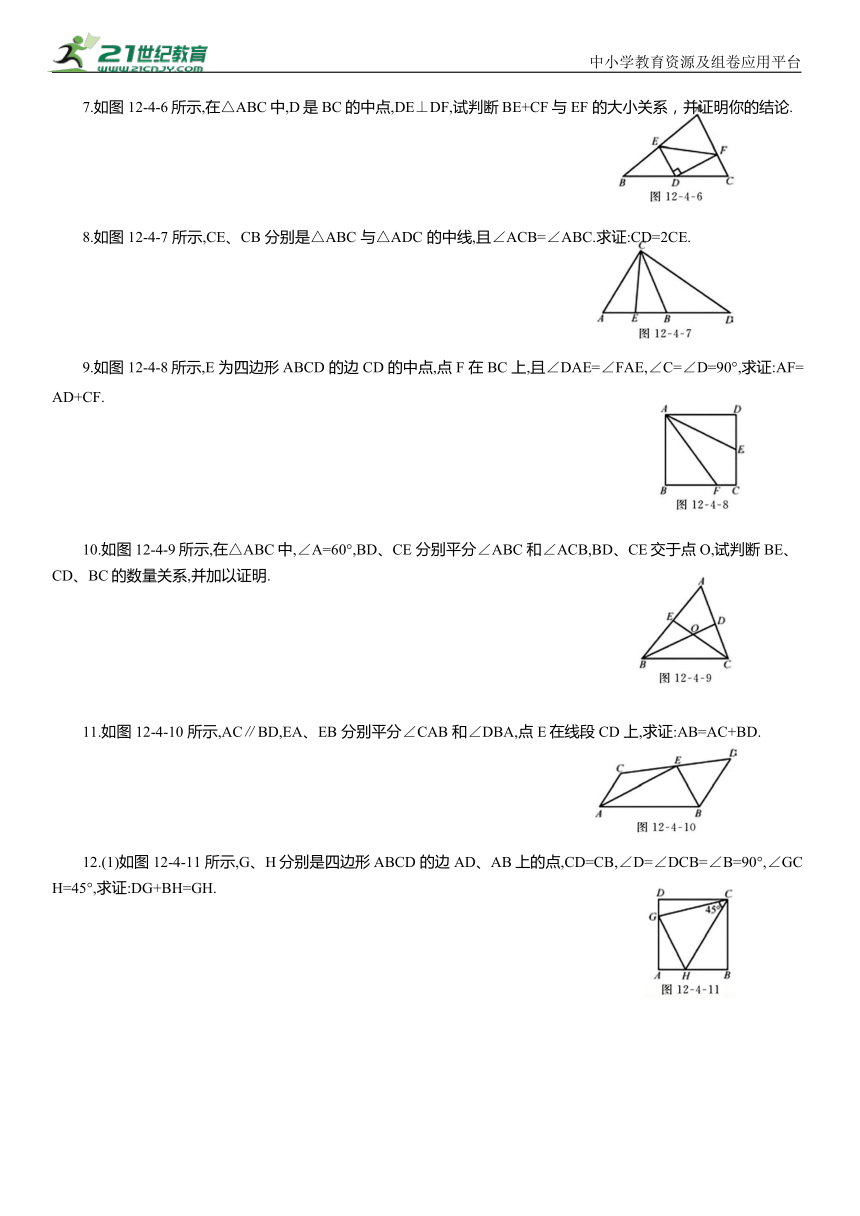
7.如图12-4-6所示,在△ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF 的大小关系,并证明你的结论.
8.如图12-4-7 所示,CE、CB 分别是△ABC 与△ADC 的中线,且∠ACB=∠ABC.求证:CD=2CE.
9.如图12-4-8所示,E 为四边形ABCD 的边CD 的中点,点 F 在 BC 上,且∠DAE=∠FAE,∠C=∠D=90°,求证:AF=AD+CF.
10.如图12-4-9所示,在△ABC中,∠A=60°,BD、CE 分别平分∠ABC 和∠ACB,BD、CE交于点O,试判断 BE、CD、BC的数量关系,并加以证明.
11.如图 12-4-10 所示,AC∥BD,EA、EB 分别平分∠CAB 和∠DBA,点 E在线段CD 上,求证:AB=AC+BD.
12.(1)如图12-4-11 所示,G、H分别是四边形ABCD 的边AD、AB上的点,CD=CB,∠D=∠DCB=∠B=90°,∠GCH=45°,求证:DG+BH=GH.
(2)如图12-4-12所示,G、H分别是四边形ABCD 的边AD、AB上的点,( ∠ C.
试探究:①GH、DG 和BH 之间的关系;
②求∠GCH的度数.
13.如图12-4-13所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD平分∠CDE.
14.如图12-4-14所示,AB=AE=CD=BC+DE=2,∠ABC=∠AED=90°,求五边形 ABCDE的面积.
15.如图12-4-15 所示,在平面直角坐标系中,将直角三角形的直角顶点放在 P(5,5)处,两条直角边与坐标轴分别交于点 A 和点B,
(1)如图12-4-15(a)所示,点A、点 B分别在x轴、y轴正半轴上运动时,试探究OA+OB 的值或取值范围.
(2)如图12-4-15(b)所示,点 A 在x 轴正半轴上运动,点 B 在y轴的负半轴时,试探究OA-OB的值或取值范围,直接写出结果.
16.如图12-4-16所示, D 为OA 的中点, 于点 F,交 AB 于点 E,( 且a、b满足 求证:
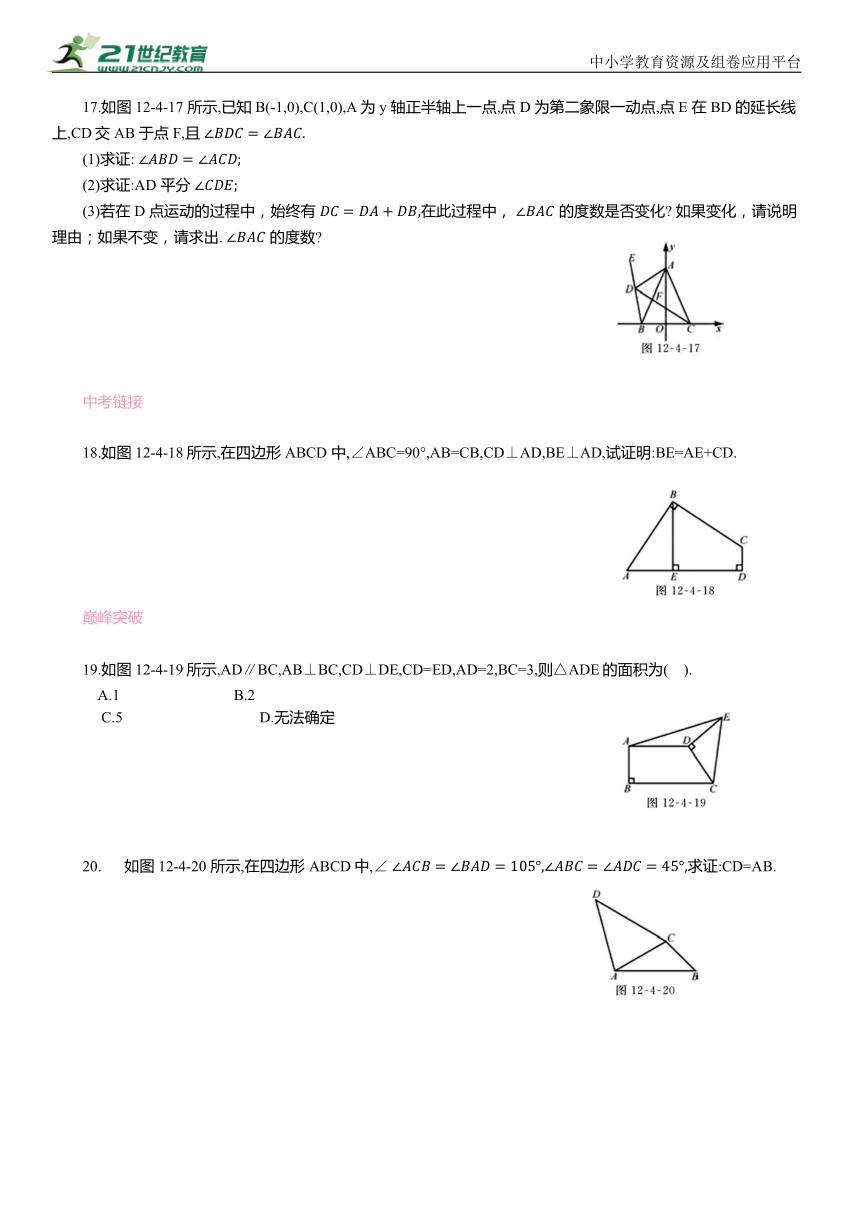
17.如图12-4-17 所示,已知B(-1,0),C(1,0),A为y 轴正半轴上一点,点 D 为第二象限一动点,点E 在 BD 的延长线上,CD交AB 于点F,且
(1)求证:
(2)求证:AD 平分
(3)若在 D 点运动的过程中,始终有 在此过程中, 的度数是否变化 如果变化,请说明理由;如果不变,请求出. 的度数
中考链接
18.如图12-4-18所示,在四边形ABCD 中,∠ABC=90°,AB=CB,CD⊥AD,BE⊥AD,试证明:BE=AE+CD.
巅峰突破
19.如图12-4-19所示,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( ).
A.1 B.2
C.5 D.无法确定
如图 12-4-20 所示,在四边形 ABCD中,∠ 求证:CD=AB.
基础演练
1. C; 2. A
3.如下图所示,连接AC、BD,
先证:△ABD≌△DCA.∴DB=AC.
再证:△ACB≌△DBC.∴∠ABC=∠DCB.
即∠B=∠C.
4.如下图所示,连接CE、BF、EB,
先证:△ABF≌△DEC.∴FB=CE.
再证:△BFE≌△ECB.
∴∠FEB=∠CBE.∴BC∥EF.
5.如下图所示,连接AC、AD,
先证:△ABC≌△AED.∴AC=AD.
∵M为CD中点,∴CM=DM.
再证:△ACM≌△ADM.∴∠AMC=∠AMD.
∵∠AMC+∠AMD=180°,
∴∠AMC=∠AMD=90°.∴AM⊥CD.
能力提升
6.如下图所示,延长CD至点E,使DE=CD,连接AE,∵D是AB的中点,∴BD=AD.
先证:△CDB≌△EDA.
∴∠DCB=∠E,BC=EA.
∴AE∥CB.∴∠BCA+∠EAC=180°.
∵∠ACB=90°,∴∠BCA=∠EAC=90°.
再证:△BCA≌△EAC.∴AB=CE.
7. BE+CF>EF.
证明:如下图所示,延长 FD 至点G,使 DG=DF,连结BG、EG,
∵D是BC中点,∴BD=CD.
又∵DE⊥DF,∴∠EDG=∠EDF=90°.
先证:△EDG≌△EDF.∴EG=EF.
再证:△FDC≌△GDB.∴CF=BG.
在△BGE中,BG+BE>EG.
∴BE+CF>EF.
8.如下图所示,延长CE至F 使EF=CE,连接BF.
∵CE为中线,∴AE=BE.
先证:△AEC≌△BEF.
∴AC=BF,∠A=∠FBE.
又∵∠ACB=∠ABC,∠DBC=∠ACB+∠A,∠FBC=∠ABC+∠EBF=∠ABC+∠A,
∴∠DBC=∠FBC.
∵AC=AB,∴AB=BF.
又∵BC为△ADC的中线,
∴AB=BD.即BF=BD.
再证:△FCB≌△DCB.
∴CF=CD.即CD=2CE.
9.如下图所示,过点 E作 EM⊥AF 于点M,连接EF.
∴∠EMA=90°.
∵∠D=90°,∴∠EMA=∠D.
先证:Rt△AME≌Rt△ADE.
∴AD=AM,DE=ME.
又∵E为CD 中点,∴DE=EC.∴ME=EC.
再证:Rt△EMF≌Rt△ECF.∴MF=FC.
又∵AF=AM+MF,∴AF=AD+FC.
10.(1)BE、CD、BC的数量关系为:BE+CD=BC.
【理由】如下图所示,在 BC上截取BF=BE,连结OF,
∵BD、CE分别平分∠ABC 和∠ACB,
∴∠1=∠2,∠3=∠4.
先证:△BEO≌△BFO.
∴EO=FO,∠EOB=∠FOB.
∵∠A+∠ABC+∠ACB=180°,
∠2+∠BOC+∠4=180°,∠A=60°,
∴∠BOC=120°.∴∠BOE=60°.
∴∠BOF=∠COF=60°.
∵∠BOE=∠COD,∴∠COD=60°.
再证:△COF≌△COD.∴CD=CF.
∵BC=BF+CF,∴BC=BE+CD.
11.如下图所示,在AB上截取AF=AC,连接EF,
∵EA平分∠CAB,∴∠1=∠2.
先证:△ACE≌△AFE.∴∠C=∠AFE.
∵AC∥BD,∴∠C+∠D=180°.
∵∠AFE+∠EFB=180°,∴∠D=∠EFB.
∵EB平分∠DBA,∴∠3=∠4.
再证:△EFB≌△EDB.∴BF=BD
∵AB=AF+BF,∴AB=AC+BD.
12.(1)如下图所示,延长AB至点 E,使BE=DG,连接CE,先证:△CDG≌△CBE.∴CG=CE,∠1=∠2.
∵∠DCB=90°,∠GCH=45°,
∴∠1+∠BCH=45°.∴∠2+∠BCH=45°.
∴∠GCH=∠ECH.
再证:△GCH≌△ECH.∴GH=EH.
∵EH=BH+BE,∴DG+BH=GH.
(2)①GH=DG+BH;②∠GCH=45°.
【证明】如下图所示,过点 C作CE⊥GH,E为垂足,
∴∠D=∠B=∠GEC=90°.
先证:△CDG≌△CEG.∴DG=EG,∠DCG=∠ECG.
再证:△CEH≌△CBH.
∴EH=BH,∠ECH=∠BCH.
①∵GH=GE+HE,∴GH=DG+BH.
②∵∠DCG+∠ECG+∠ECH+∠BCH=90°,
∴2(∠GCE+∠ECH)=90°.
∴∠GCE+∠ECH=45°.即∠GCH=45°.
13.如下图所示,延长DE 至点 F,使 EF=BC,连接AC、AF,
∵∠ABC+∠AED=180°,∠AEF+∠AED=180°,
∴∠ABC=∠AEF.
先证:△ABC≌△AEF.∴AC=AF.
∵BC+DE=CD,∴EF+DE=CD.
即 DC=DF.
再证:△ACD≌△AFD.
∴∠ADC=∠ADF.∴AD 平分∠CDE.
14.如下图所示,延长 DE 至点 H,使 EH=BC,连接AC、AD、AH.
先证:△ABC≌△AEH.∴AC=AH.
∵BC+DE=2,
∴DH=DE+EH=BC+DE=2.
∵CD=BC+DE,∴CD=DH.
再证:△ADC≌△ADH.
∴S五边形ABCDE=S四边形AHDC=2S△ADH
15.(1)如下图所示,过点 P 作 PM⊥OA,PN⊥OB 分别交x轴于点M,y轴于点 N,
∵P(5,5),
∴∠PNB=∠PMA,PN=PM=OM=ON=5.
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2.
证明△PNB≌△PMA.∴NB=MA.
∵OB=ON-NB,OA=OM+MA,
∴OA+OB=ON-NB+OM+MA=2OM=10.
∴OA+OB的值不变.
(2)OA-OB=10.
16.由题意可求:a=4,b=4.
∴OB=AO.
∵∠AOB=90°,∴∠OAB=∠OBA=45°.
如下图所示,过点 A作AG⊥OA交OE 的延长线于点 G,即∠OAG=90°.
∵OE⊥BD,∴∠BFO=90°.∴∠1+∠BOF=90°.
∵∠2+∠BOF=90°,∴∠1=∠2.
先证:△BOD≌△OAG.
∴∠BDO=∠G,OD=AG.
∵D为OA 的中点,∴OD=AD.∴AD=AG.
∵AG⊥OA,∠BAO=45°,∴∠EAO=∠EAG.
再证:△EAD≌△EAG.
∴∠EDA=∠G.∴∠BDO=∠EDA.
17.(1)∵∠BDC=∠BAC,∠BFD=∠AFC,∴∠ABD=∠ACD.
(2)如下图所示,过点 A 作AM⊥CD于点M,作 AN⊥BE于点 N.则∠AMC=∠ANB=90°.
∵OB=OC,∠AOB=∠AOC,AO=AO,
∴△AOB≌△AOC(SAS),∴AB=AC.
∵∠ABD=∠ACD,AB=AC,
∴△ACM≌△ABN(AAS).∴AM=AN.
∴AD平分∠CDE.
(3)∠BAC不变化.如下图所示,在CD上截CP=BD,连接AP,
∵CD=AD+BD,∴AD=PD,
∵AB=AC,∠ABD=∠ACD,BD=CP,
∴△ABD≌△ACP.∴AD=AP;∠BAD=∠CAP.
∴AD=AP=PD,
∴△ADP是等边三角形,∴∠DAP=60°,
∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.
中考链接
18.如下图所示,过点 B作BE⊥DC交 DC的延长线于点 F,
∴∠EBF+∠BED=180°,∠F+∠D=180°.
∵CD⊥AD,BE⊥AD,
∴∠BED=∠BEA=∠D=90°.
∴∠EBF=∠F=∠BEA=90°..
∴∠2+∠3=90°.
∵∠ABC=90°,∴∠1+∠3=90°.
∴∠1=∠2.
∵AB=CB,∴△ABE≌△CBF(AAS).
∴AE=CF.
∵BF∥ED,CD⊥AD,BE⊥AD,∴BE=DF.
∵DF=CF+CD,∴BE=AE+CD.
巅峰突破
19. A
20.如下图所示,过点 A 作AE⊥AB交 BC的延长线于点 E,
∴∠EAB=90°.
∵∠ABC=∠ADC=45°,∠ABC+∠E=90°,
∴∠ADC=∠E=45°.∴AE=AB.
∵∠ACB=105°,∠ACB+∠ECA=180°,
∴∠ECA=75°.
∵∠ABC=45°,∠CAB+∠ACB+∠ABC=180°,
∴∠CAB=30°.
∵∠BAD=105°,∴∠DAC=75°.
∴∠DAC=∠ECA.
∵AC=CA,∴△DAC≌△ECA(AAS).
∴AE=CD.
∵AE=AB,∴CD=AB.
一、课标导航
课标内容 课标要求 目标层次
全等的构造 全等三角形的常见辅助线的添加方法 ★
掌握全等三角形的辅助线的添加方法,并提高解决实际问题的能力
二、核心纲要
1.添加辅助线的方法和语言表述
(1)作线段:连接…….
(2)作平行线:过点……作……//……
(3)作垂线(作高):过点……作……⊥……,垂足为…
(4)作中线:取……中点……,连接…….
(5)延长并截取线段:延长……使……等于…
(6)截取等长线段:在······上截取······,使······等于······.
(7)作角平分线:作……平分……作角……等于已知角……
(8)作一个角等于已知角:作角……等于……
2.全等三角形中的基本图形的构造与运用
常用的辅助线的添加方法:
(1)倍长中线(或类中线)法:若遇到三角形的中线或类中线(与中点有关的线段),通常考虑倍长中线或类中线(与中点有关的线段),构造全等三角形.
(2)截长补短法:若遇到证明线段的和、差、倍、分关系时,通常考虑截长补短法,构造全等三角形.
①截长:在较长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;
②补短:将一条较短线段延长,延长部分等于另一条较短线段,然后证明新线段等于较长线段;或延长一条较短线段等于较长线段,然后证明延长部分等于另一条较短线段.
(3)有的题目需要根据几何图形的特殊性或题目中的条件和结论考虑添加辅助线.
3.基本模型
中小学教育资源及组卷应用平台
本节重点讲解:辅助线的作法及应用.
三、全能突破
基础演练
1.已知,AD 是△ABC中BC边上的中线,若AB=4,AC=6,则AD的取值范围是( ).
A. AD>1 B. AD<5
C.1
A.50 B.62
C.65 D.68
3.如图12-4-2所示,AB=DC,∠A=∠D,求证:∠B=∠C.
4.如图12-4-3所示,已知∠A=∠D,AB=DE,AF=DC,EF=BC.求证:BC∥EF.
5.如图12-4-4所示,在凸五边形中, ,M为CD 中点.求证:
能力提升
6.如图12-4-5所示,D 是AB 的中点, 求证:
7.如图12-4-6所示,在△ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF 的大小关系,并证明你的结论.
8.如图12-4-7 所示,CE、CB 分别是△ABC 与△ADC 的中线,且∠ACB=∠ABC.求证:CD=2CE.
9.如图12-4-8所示,E 为四边形ABCD 的边CD 的中点,点 F 在 BC 上,且∠DAE=∠FAE,∠C=∠D=90°,求证:AF=AD+CF.
10.如图12-4-9所示,在△ABC中,∠A=60°,BD、CE 分别平分∠ABC 和∠ACB,BD、CE交于点O,试判断 BE、CD、BC的数量关系,并加以证明.
11.如图 12-4-10 所示,AC∥BD,EA、EB 分别平分∠CAB 和∠DBA,点 E在线段CD 上,求证:AB=AC+BD.
12.(1)如图12-4-11 所示,G、H分别是四边形ABCD 的边AD、AB上的点,CD=CB,∠D=∠DCB=∠B=90°,∠GCH=45°,求证:DG+BH=GH.
(2)如图12-4-12所示,G、H分别是四边形ABCD 的边AD、AB上的点,( ∠ C.
试探究:①GH、DG 和BH 之间的关系;
②求∠GCH的度数.
13.如图12-4-13所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD平分∠CDE.
14.如图12-4-14所示,AB=AE=CD=BC+DE=2,∠ABC=∠AED=90°,求五边形 ABCDE的面积.
15.如图12-4-15 所示,在平面直角坐标系中,将直角三角形的直角顶点放在 P(5,5)处,两条直角边与坐标轴分别交于点 A 和点B,
(1)如图12-4-15(a)所示,点A、点 B分别在x轴、y轴正半轴上运动时,试探究OA+OB 的值或取值范围.
(2)如图12-4-15(b)所示,点 A 在x 轴正半轴上运动,点 B 在y轴的负半轴时,试探究OA-OB的值或取值范围,直接写出结果.
16.如图12-4-16所示, D 为OA 的中点, 于点 F,交 AB 于点 E,( 且a、b满足 求证:
17.如图12-4-17 所示,已知B(-1,0),C(1,0),A为y 轴正半轴上一点,点 D 为第二象限一动点,点E 在 BD 的延长线上,CD交AB 于点F,且
(1)求证:
(2)求证:AD 平分
(3)若在 D 点运动的过程中,始终有 在此过程中, 的度数是否变化 如果变化,请说明理由;如果不变,请求出. 的度数
中考链接
18.如图12-4-18所示,在四边形ABCD 中,∠ABC=90°,AB=CB,CD⊥AD,BE⊥AD,试证明:BE=AE+CD.
巅峰突破
19.如图12-4-19所示,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( ).
A.1 B.2
C.5 D.无法确定
如图 12-4-20 所示,在四边形 ABCD中,∠ 求证:CD=AB.
基础演练
1. C; 2. A
3.如下图所示,连接AC、BD,
先证:△ABD≌△DCA.∴DB=AC.
再证:△ACB≌△DBC.∴∠ABC=∠DCB.
即∠B=∠C.
4.如下图所示,连接CE、BF、EB,
先证:△ABF≌△DEC.∴FB=CE.
再证:△BFE≌△ECB.
∴∠FEB=∠CBE.∴BC∥EF.
5.如下图所示,连接AC、AD,
先证:△ABC≌△AED.∴AC=AD.
∵M为CD中点,∴CM=DM.
再证:△ACM≌△ADM.∴∠AMC=∠AMD.
∵∠AMC+∠AMD=180°,
∴∠AMC=∠AMD=90°.∴AM⊥CD.
能力提升
6.如下图所示,延长CD至点E,使DE=CD,连接AE,∵D是AB的中点,∴BD=AD.
先证:△CDB≌△EDA.
∴∠DCB=∠E,BC=EA.
∴AE∥CB.∴∠BCA+∠EAC=180°.
∵∠ACB=90°,∴∠BCA=∠EAC=90°.
再证:△BCA≌△EAC.∴AB=CE.
7. BE+CF>EF.
证明:如下图所示,延长 FD 至点G,使 DG=DF,连结BG、EG,
∵D是BC中点,∴BD=CD.
又∵DE⊥DF,∴∠EDG=∠EDF=90°.
先证:△EDG≌△EDF.∴EG=EF.
再证:△FDC≌△GDB.∴CF=BG.
在△BGE中,BG+BE>EG.
∴BE+CF>EF.
8.如下图所示,延长CE至F 使EF=CE,连接BF.
∵CE为中线,∴AE=BE.
先证:△AEC≌△BEF.
∴AC=BF,∠A=∠FBE.
又∵∠ACB=∠ABC,∠DBC=∠ACB+∠A,∠FBC=∠ABC+∠EBF=∠ABC+∠A,
∴∠DBC=∠FBC.
∵AC=AB,∴AB=BF.
又∵BC为△ADC的中线,
∴AB=BD.即BF=BD.
再证:△FCB≌△DCB.
∴CF=CD.即CD=2CE.
9.如下图所示,过点 E作 EM⊥AF 于点M,连接EF.
∴∠EMA=90°.
∵∠D=90°,∴∠EMA=∠D.
先证:Rt△AME≌Rt△ADE.
∴AD=AM,DE=ME.
又∵E为CD 中点,∴DE=EC.∴ME=EC.
再证:Rt△EMF≌Rt△ECF.∴MF=FC.
又∵AF=AM+MF,∴AF=AD+FC.
10.(1)BE、CD、BC的数量关系为:BE+CD=BC.
【理由】如下图所示,在 BC上截取BF=BE,连结OF,
∵BD、CE分别平分∠ABC 和∠ACB,
∴∠1=∠2,∠3=∠4.
先证:△BEO≌△BFO.
∴EO=FO,∠EOB=∠FOB.
∵∠A+∠ABC+∠ACB=180°,
∠2+∠BOC+∠4=180°,∠A=60°,
∴∠BOC=120°.∴∠BOE=60°.
∴∠BOF=∠COF=60°.
∵∠BOE=∠COD,∴∠COD=60°.
再证:△COF≌△COD.∴CD=CF.
∵BC=BF+CF,∴BC=BE+CD.
11.如下图所示,在AB上截取AF=AC,连接EF,
∵EA平分∠CAB,∴∠1=∠2.
先证:△ACE≌△AFE.∴∠C=∠AFE.
∵AC∥BD,∴∠C+∠D=180°.
∵∠AFE+∠EFB=180°,∴∠D=∠EFB.
∵EB平分∠DBA,∴∠3=∠4.
再证:△EFB≌△EDB.∴BF=BD
∵AB=AF+BF,∴AB=AC+BD.
12.(1)如下图所示,延长AB至点 E,使BE=DG,连接CE,先证:△CDG≌△CBE.∴CG=CE,∠1=∠2.
∵∠DCB=90°,∠GCH=45°,
∴∠1+∠BCH=45°.∴∠2+∠BCH=45°.
∴∠GCH=∠ECH.
再证:△GCH≌△ECH.∴GH=EH.
∵EH=BH+BE,∴DG+BH=GH.
(2)①GH=DG+BH;②∠GCH=45°.
【证明】如下图所示,过点 C作CE⊥GH,E为垂足,
∴∠D=∠B=∠GEC=90°.
先证:△CDG≌△CEG.∴DG=EG,∠DCG=∠ECG.
再证:△CEH≌△CBH.
∴EH=BH,∠ECH=∠BCH.
①∵GH=GE+HE,∴GH=DG+BH.
②∵∠DCG+∠ECG+∠ECH+∠BCH=90°,
∴2(∠GCE+∠ECH)=90°.
∴∠GCE+∠ECH=45°.即∠GCH=45°.
13.如下图所示,延长DE 至点 F,使 EF=BC,连接AC、AF,
∵∠ABC+∠AED=180°,∠AEF+∠AED=180°,
∴∠ABC=∠AEF.
先证:△ABC≌△AEF.∴AC=AF.
∵BC+DE=CD,∴EF+DE=CD.
即 DC=DF.
再证:△ACD≌△AFD.
∴∠ADC=∠ADF.∴AD 平分∠CDE.
14.如下图所示,延长 DE 至点 H,使 EH=BC,连接AC、AD、AH.
先证:△ABC≌△AEH.∴AC=AH.
∵BC+DE=2,
∴DH=DE+EH=BC+DE=2.
∵CD=BC+DE,∴CD=DH.
再证:△ADC≌△ADH.
∴S五边形ABCDE=S四边形AHDC=2S△ADH
15.(1)如下图所示,过点 P 作 PM⊥OA,PN⊥OB 分别交x轴于点M,y轴于点 N,
∵P(5,5),
∴∠PNB=∠PMA,PN=PM=OM=ON=5.
∵∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2.
证明△PNB≌△PMA.∴NB=MA.
∵OB=ON-NB,OA=OM+MA,
∴OA+OB=ON-NB+OM+MA=2OM=10.
∴OA+OB的值不变.
(2)OA-OB=10.
16.由题意可求:a=4,b=4.
∴OB=AO.
∵∠AOB=90°,∴∠OAB=∠OBA=45°.
如下图所示,过点 A作AG⊥OA交OE 的延长线于点 G,即∠OAG=90°.
∵OE⊥BD,∴∠BFO=90°.∴∠1+∠BOF=90°.
∵∠2+∠BOF=90°,∴∠1=∠2.
先证:△BOD≌△OAG.
∴∠BDO=∠G,OD=AG.
∵D为OA 的中点,∴OD=AD.∴AD=AG.
∵AG⊥OA,∠BAO=45°,∴∠EAO=∠EAG.
再证:△EAD≌△EAG.
∴∠EDA=∠G.∴∠BDO=∠EDA.
17.(1)∵∠BDC=∠BAC,∠BFD=∠AFC,∴∠ABD=∠ACD.
(2)如下图所示,过点 A 作AM⊥CD于点M,作 AN⊥BE于点 N.则∠AMC=∠ANB=90°.
∵OB=OC,∠AOB=∠AOC,AO=AO,
∴△AOB≌△AOC(SAS),∴AB=AC.
∵∠ABD=∠ACD,AB=AC,
∴△ACM≌△ABN(AAS).∴AM=AN.
∴AD平分∠CDE.
(3)∠BAC不变化.如下图所示,在CD上截CP=BD,连接AP,
∵CD=AD+BD,∴AD=PD,
∵AB=AC,∠ABD=∠ACD,BD=CP,
∴△ABD≌△ACP.∴AD=AP;∠BAD=∠CAP.
∴AD=AP=PD,
∴△ADP是等边三角形,∴∠DAP=60°,
∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.
中考链接
18.如下图所示,过点 B作BE⊥DC交 DC的延长线于点 F,
∴∠EBF+∠BED=180°,∠F+∠D=180°.
∵CD⊥AD,BE⊥AD,
∴∠BED=∠BEA=∠D=90°.
∴∠EBF=∠F=∠BEA=90°..
∴∠2+∠3=90°.
∵∠ABC=90°,∴∠1+∠3=90°.
∴∠1=∠2.
∵AB=CB,∴△ABE≌△CBF(AAS).
∴AE=CF.
∵BF∥ED,CD⊥AD,BE⊥AD,∴BE=DF.
∵DF=CF+CD,∴BE=AE+CD.
巅峰突破
19. A
20.如下图所示,过点 A 作AE⊥AB交 BC的延长线于点 E,
∴∠EAB=90°.
∵∠ABC=∠ADC=45°,∠ABC+∠E=90°,
∴∠ADC=∠E=45°.∴AE=AB.
∵∠ACB=105°,∠ACB+∠ECA=180°,
∴∠ECA=75°.
∵∠ABC=45°,∠CAB+∠ACB+∠ABC=180°,
∴∠CAB=30°.
∵∠BAD=105°,∴∠DAC=75°.
∴∠DAC=∠ECA.
∵AC=CA,∴△DAC≌△ECA(AAS).
∴AE=CD.
∵AE=AB,∴CD=AB.
