11.2 与三角形有关的角 培优训练(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 11.2 与三角形有关的角 培优训练(含答案)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 827.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览



文档简介
11.2 与三角形有关的角
一、课标导航
课标内容 课标要求 目标层次
三角形的内角 理解三角形的内角的概念 ★
掌握三角形的内角和定理,并进行简单的推理和计算 ★★
三角形的外角 理解三角形的外角的概念 ★
掌握三角形的外角的性质,并进行简单的推理和计算 7
二、核心纲要
1.三角形内角和定理及其应用
(1)三角形内角和定理:三角形三个内角的和是
(2)三角形内角和定理的应用
①在三角形中已知两角可求第三角,或已知各角之间关系,求各角;
②证明角之间的关系.
2.三角形的外角
(1)定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角.
(2)性质:三角形的一个外角等于与它不相邻的两个内角之和.
三角形的一个外角大于与它不相邻的任何一个内角.
(3)三角形外角和定理:三角形外角和是
(4)三角形外角的性质的应用
①已知外角和与它不相邻两个内角中的一个可求“另一个”;
②可证一个角等于另两个角的和;
③利用它作为中间关系式证明两个角相等;
④利用它证明角的不等关系.
3.思想方法
(1)分类讨论.
(2)方程思想.
本节重点讲解:一个性质(外角的性质),两大定理(三角形内、外角和定理),两个思想,四个模型(“小旗”模型,“飞镖”模型,“8”字模型和角平分线相关模型).
三、全能突破
基础演练
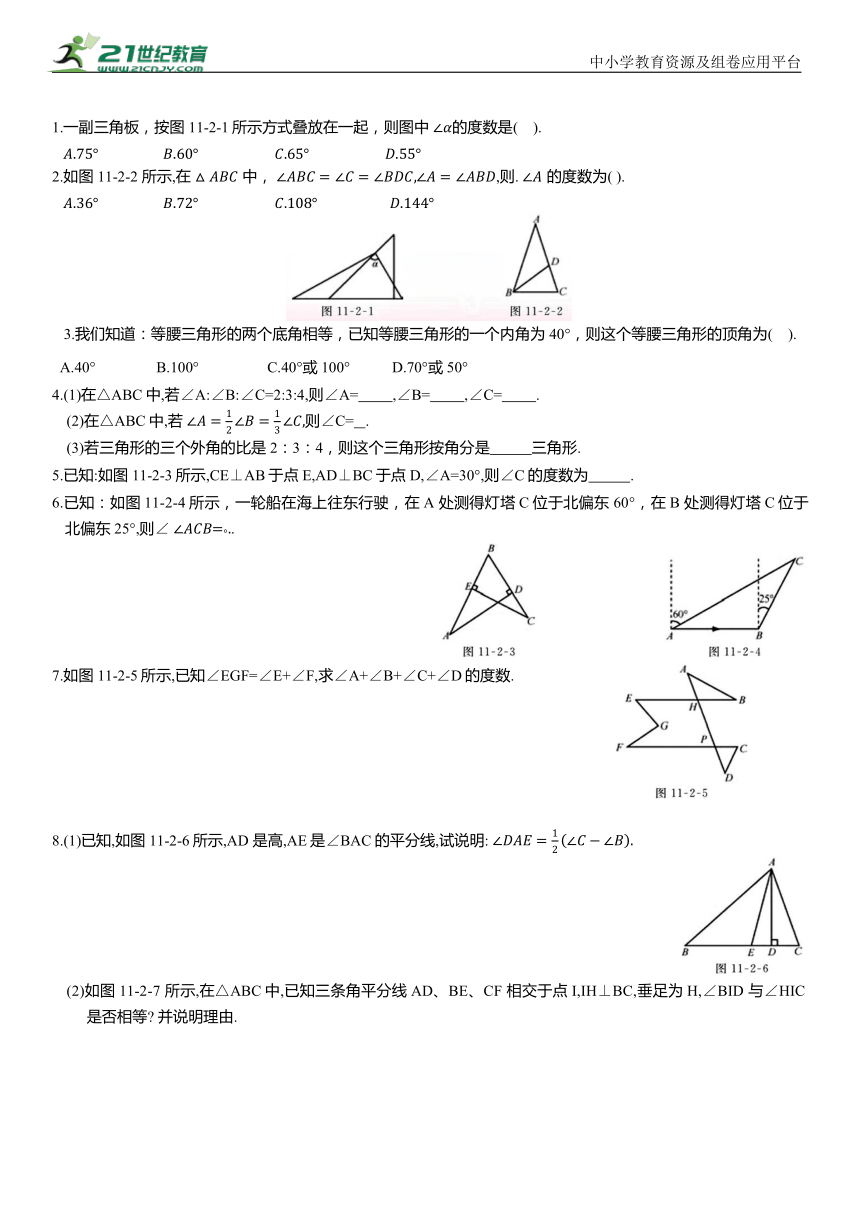
1.一副三角板,按图11-2-1所示方式叠放在一起,则图中 的度数是( ).
2.如图11-2-2 所示,在 中, ,则. 的度数为( ).
3.我们知道:等腰三角形的两个底角相等,已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( ).
A.40° B.100° C.40°或100° D.70°或50°
4.(1)在△ABC中,若∠A:∠B:∠C=2:3:4,则∠A= ,∠B= ,∠C= .
(2)在△ABC中,若 则∠C= .
(3)若三角形的三个外角的比是2:3:4,则这个三角形按角分是 三角形.
5.已知:如图11-2-3所示,CE⊥AB于点E,AD⊥BC于点D,∠A=30°,则∠C的度数为 .
6.已知:如图11-2-4所示,一轮船在海上往东行驶,在A 处测得灯塔C位于北偏东 60°,在B 处测得灯塔C位于北偏东 25°,则∠ .
7.如图11-2-5所示,已知∠EGF=∠E+∠F,求∠A+∠B+∠C+∠D的度数.
8.(1)已知,如图11-2-6所示,AD 是高,AE是∠BAC的平分线,试说明:
(2)如图11-2-7 所示,在△ABC中,已知三条角平分线AD、BE、CF 相交于点I,IH⊥BC,垂足为H,∠BID 与∠HIC 是否相等 并说明理由.
能力提升
9.在三角形中,最大角α的取值范围是( ).
中小学教育资源及组卷应用平台
A.0°<α<90° B.60°<α<180° C.60°≤α<90° D.60°≤α<180°
10.直角三角形中两锐角平分线所成的角的度数是( ).
A.45° B.135° 或 D.都不对
11.如图11-2-8所示,把△ABC纸片沿DE 折叠,当点 A 落在四边形BCDE 内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,那么,你发现的规律是( ).
A.∠A=∠1+∠2
12.已知△ABC的三个内角为∠A、∠B、∠C,且α C则α,β,γ中,锐角的个数最多为( ).
A.0 B.1 C.2 D.3
13.在△ABC中,BC边不动,点A 竖直向上运动,∠A 越来越小, 越来越大,若 减少α,∠B增加β,∠C增加γ,则α,β,γ三者之间的关系是 .
14.在△ABC 中,高BD、CE 所在的直线相交于点H,且点 H 与点B、C 不重合,∠A=50°,则∠BHC= .
15.已知等腰三角形一腰上的高与另一腰成20°角,则这个三角形的顶角是 .
16.如图11-2-9 所示,在△ABC中,A B平分∠ABC,A C平分∠ACD,A B平分∠A BD,A C平分∠A CD,A B 平分. 平分∠A CD,若∠A=64°,则. 依此类推,若
17.(a)如图11-2-10 所示,在△ABC中,∠ABC的n等分线与∠ACB的n等分线分别相交于( G ,…,G ,试猜想: 与∠A的关系.(其中n是不小于2的整数).首先得到:当n=2时,如图(a)所示, 当n=3时,如图(b)所示, 如图(c)所示,猜想
(2)如图(d)所示,在四边形ABCD 中,BP、CP 仍然是 的角平分线,则∠P 与∠A,∠D之间的数量关系为 .
18.如图11-2-11 所示,在△ABC中,AD⊥BC,AE平分. CG是△ABC的外角∠ACF 的平分线,若∠G--∠DAE=60°,则∠ACB = .
19.阅读材料:如图11-2-12所示,AD与CB 相交于O 点,在 和 中, 180°,∠C+∠D+∠COD=180°,∠AOB=∠COD,所以, 图形类似于数字“8”,所以我们称之为“8”字形.
根据上述材料解决下列问题:
如图11-2-13所示,BE平分∠ABC,DE平分. ,BE 与AD 相交于点G,BC 与DE 相交于点 H.
(1)仔细观察图 11-2-13 中有 个“8”字形.
(2)求 的度数.
(3)试探究 之间的关系.(直接写出结论)
20.如图11-2-14 所示,已知射线OM与射线ON 互相垂直,B、A分别为OM、ON上一动点,
(1)若 的平分线交于点C.问:点B、A在OM、ON上运动过程中,∠C 的度数是否改变 若不改变,直接写出结论;若改变,说明理由.
(2)如图11-2-15所示,若∠ABO、∠BAN的平分线所在的直线相交于点C,其他条件不变,(1)中的结论是否成立 若成立,求出其值;若不成立,说明理由.
21.如图11-2-16所示,在△ADE和△ABC中,∠EAD=∠AED=∠BAC=∠BCA=45°,∠BAD=∠BCF.
(1)求∠ECF+∠DAC+∠ECA的度数;
(2)判断ED与FC 的位置关系,并对你的结论加以证明.
22.如图11-2-17(a)所示,在平面直角坐标系中,△DEQ的一个顶点在x轴的负半轴上,边DQ交x 轴于点C,且CE 平分∠DEQ,过点 D 作直线交x 轴于点 B,交 y 轴于点 A,使∠ADE=∠BDC,已知C(m,0),E(n,0),其中m,n满足|
(1)求点 C、E的坐标.
(2)若∠ABC=30°,求∠Q的度数.
(3)如图11-2-17(b)所示,在平面直角坐标系中,若直线AB绕点 D 旋转,过 D 作DH⊥AB,交x轴于点G,交y轴于点 H.直线AB绕点D 转动时,下列结论:①∠Q的大小不变; 的值不变.选择一个正确的结论,求其值,并证明你的结论.
23.将一副常规的三角尺按图11-2-18所示方式放置,则图中 的度数为( ).
A.75° B.95°
24.一副三角板叠在一起,按图11-2-19所示方式放置,最小锐角的顶点 D 恰好放在等腰直角三角板的斜边AB上,BC 与DE 交于点M.如果 ,那么. 的度数为 .
巅峰突破
25. 如图 11-2-20 所示, 在 中, 则射线 AF 与BG( ).
A.平行 B.延长后相交
C.反向延长后相交 D.可能平行也可能相交
如图 11-2-21所示,DC平分∠ADB,EC平分∠AEB,若 则∠C= .(用α、β表示)
基础演练
1. A; 2. A; 3. C 4.(1)40°,60°,80°;
(2)90°;(3)钝角
5.30°; 6.35°
7.如下图所示,过点G作GM∥BE,
∴∠1=∠E.
∵∠EGF=∠E+∠F=∠1+∠2,
∴∠F=∠2.∴BE∥MG∥FC.
∴∠BHP+∠CPH=180°.
∵∠BHD是△ABH的一个外角,
∴∠BHD=∠A+∠B.
同理可证:∠CPA=∠C+∠D.
∴∠A+∠B+∠C+∠D=180°.
8.(1)∵AE平分∠BAC,
∵∠BAC+∠B+∠C=180°,
∵AD⊥BC,∴∠DAC=90°-∠C.
(2)∠BID=∠HIC.
【理由】∵AD、BE、CF为△ABC的角平分线,
∵∠BID 是△ABI的一个外角,
∵IH⊥BC,∴∠IHC=90°.
∴∠BID=∠HIC.
能力提升
9. D; 10. C; 11. B; 12. B; 13.α=β+γ.
14.130°或50°. 15.70°或110°. 16.8°;2
18.如下图所示,延长 BA,可证 AG 平分∠CAH,利用模型(5)可得:
又可证: 进而求出∠ACB=60°.
19.(1)6个.
(2)由材料可得:∠A+∠ABE=∠E+∠EDG.①
∠E+∠EBC=∠C+∠CDE.②
①+②得:∠A+∠ABE+∠C+∠CDE=∠E+∠EDG+∠E+∠EBC.
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC,∠CDE=∠EDG.
∴∠A+∠C=2∠E.
∵∠A=48°,∠C=46°,∴∠E=47°,
(3)由(2)可得:∠A+∠C=2∠E.
20.(1)∠C的度数不会改变,且∠C=45°.
(2)成立.
∵∠DAB是∠CAB的一个外角,
∴∠DAB=∠C+∠CBA.
∴2∠DAB=2∠C+2∠CBA.
∵∠NAB是△AOB的一个外角,
∴∠NAB=∠O+∠ABO.
∵AD平分∠NAB,BC平分∠ABO,
∴∠NAB=2∠DAB,∠ABO=2∠CBA.
∴2∠DAB=∠O+2∠CBA
21.(1)∵∠ECF=∠ECB+∠BCF,∠BCF=∠BAD,
∴∠ECF=∠BAD+∠ECB.
∴∠ECF+∠DAC+∠ECA
=(∠ECB+∠BAD)+∠DAC+∠ECA
=(∠ECB+∠ECA)+(∠DAC+∠BAD)
=∠BCA+∠BAC.
∵∠BAC=∠BCA=45°,
∴∠ECF+∠DAC+∠ECA=90°.
(2)ED∥FC.理由如下:
如下图所示,延长AD、CF交于点G,由(1)可证:∠G=90°,
∵∠EAD=∠AED=45°,∴∠EDA=90°.
∴∠EDG=90°.
∴∠EDG=∠G.∴DE∥CF.
22.(1)C(3,0),E(-4,0)
(2)如下图所示,延长ED至点F,则∠ADE=∠BDF.
又∵∠ADE=∠BDC,∴∠BDF=∠BDC.
∵CE平分∠DEQ,∴∠DEB=∠QEB.
∴2∠BDF=2∠ABC+∠DEQ,
即∠FDQ=2∠ABC+∠DEQ.
∵∠FDQ=∠Q+∠DEQ,
∴∠Q=2∠ABC=2×30°=60°.
(3)②正确.
理由:在直线 AB 绕点 D 旋转的过程中,CE 仍平分∠DEQ,BD 仍是△EDQ的外角平分线,
由(2)可知:∠Q=2∠ABC.
∵DH⊥AB,∴∠HDB=∠HOG=90°.
∵∠OGH=∠DGB,∴∠OHD=∠ABC.
中考链接
23. C; 24.85°
巅峰突破
25. A; 26.α+β
一、课标导航
课标内容 课标要求 目标层次
三角形的内角 理解三角形的内角的概念 ★
掌握三角形的内角和定理,并进行简单的推理和计算 ★★
三角形的外角 理解三角形的外角的概念 ★
掌握三角形的外角的性质,并进行简单的推理和计算 7
二、核心纲要
1.三角形内角和定理及其应用
(1)三角形内角和定理:三角形三个内角的和是
(2)三角形内角和定理的应用
①在三角形中已知两角可求第三角,或已知各角之间关系,求各角;
②证明角之间的关系.
2.三角形的外角
(1)定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角.
(2)性质:三角形的一个外角等于与它不相邻的两个内角之和.
三角形的一个外角大于与它不相邻的任何一个内角.
(3)三角形外角和定理:三角形外角和是
(4)三角形外角的性质的应用
①已知外角和与它不相邻两个内角中的一个可求“另一个”;
②可证一个角等于另两个角的和;
③利用它作为中间关系式证明两个角相等;
④利用它证明角的不等关系.
3.思想方法
(1)分类讨论.
(2)方程思想.
本节重点讲解:一个性质(外角的性质),两大定理(三角形内、外角和定理),两个思想,四个模型(“小旗”模型,“飞镖”模型,“8”字模型和角平分线相关模型).
三、全能突破
基础演练
1.一副三角板,按图11-2-1所示方式叠放在一起,则图中 的度数是( ).
2.如图11-2-2 所示,在 中, ,则. 的度数为( ).
3.我们知道:等腰三角形的两个底角相等,已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( ).
A.40° B.100° C.40°或100° D.70°或50°
4.(1)在△ABC中,若∠A:∠B:∠C=2:3:4,则∠A= ,∠B= ,∠C= .
(2)在△ABC中,若 则∠C= .
(3)若三角形的三个外角的比是2:3:4,则这个三角形按角分是 三角形.
5.已知:如图11-2-3所示,CE⊥AB于点E,AD⊥BC于点D,∠A=30°,则∠C的度数为 .
6.已知:如图11-2-4所示,一轮船在海上往东行驶,在A 处测得灯塔C位于北偏东 60°,在B 处测得灯塔C位于北偏东 25°,则∠ .
7.如图11-2-5所示,已知∠EGF=∠E+∠F,求∠A+∠B+∠C+∠D的度数.
8.(1)已知,如图11-2-6所示,AD 是高,AE是∠BAC的平分线,试说明:
(2)如图11-2-7 所示,在△ABC中,已知三条角平分线AD、BE、CF 相交于点I,IH⊥BC,垂足为H,∠BID 与∠HIC 是否相等 并说明理由.
能力提升
9.在三角形中,最大角α的取值范围是( ).
中小学教育资源及组卷应用平台
A.0°<α<90° B.60°<α<180° C.60°≤α<90° D.60°≤α<180°
10.直角三角形中两锐角平分线所成的角的度数是( ).
A.45° B.135° 或 D.都不对
11.如图11-2-8所示,把△ABC纸片沿DE 折叠,当点 A 落在四边形BCDE 内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,那么,你发现的规律是( ).
A.∠A=∠1+∠2
12.已知△ABC的三个内角为∠A、∠B、∠C,且α C则α,β,γ中,锐角的个数最多为( ).
A.0 B.1 C.2 D.3
13.在△ABC中,BC边不动,点A 竖直向上运动,∠A 越来越小, 越来越大,若 减少α,∠B增加β,∠C增加γ,则α,β,γ三者之间的关系是 .
14.在△ABC 中,高BD、CE 所在的直线相交于点H,且点 H 与点B、C 不重合,∠A=50°,则∠BHC= .
15.已知等腰三角形一腰上的高与另一腰成20°角,则这个三角形的顶角是 .
16.如图11-2-9 所示,在△ABC中,A B平分∠ABC,A C平分∠ACD,A B平分∠A BD,A C平分∠A CD,A B 平分. 平分∠A CD,若∠A=64°,则. 依此类推,若
17.(a)如图11-2-10 所示,在△ABC中,∠ABC的n等分线与∠ACB的n等分线分别相交于( G ,…,G ,试猜想: 与∠A的关系.(其中n是不小于2的整数).首先得到:当n=2时,如图(a)所示, 当n=3时,如图(b)所示, 如图(c)所示,猜想
(2)如图(d)所示,在四边形ABCD 中,BP、CP 仍然是 的角平分线,则∠P 与∠A,∠D之间的数量关系为 .
18.如图11-2-11 所示,在△ABC中,AD⊥BC,AE平分. CG是△ABC的外角∠ACF 的平分线,若∠G--∠DAE=60°,则∠ACB = .
19.阅读材料:如图11-2-12所示,AD与CB 相交于O 点,在 和 中, 180°,∠C+∠D+∠COD=180°,∠AOB=∠COD,所以, 图形类似于数字“8”,所以我们称之为“8”字形.
根据上述材料解决下列问题:
如图11-2-13所示,BE平分∠ABC,DE平分. ,BE 与AD 相交于点G,BC 与DE 相交于点 H.
(1)仔细观察图 11-2-13 中有 个“8”字形.
(2)求 的度数.
(3)试探究 之间的关系.(直接写出结论)
20.如图11-2-14 所示,已知射线OM与射线ON 互相垂直,B、A分别为OM、ON上一动点,
(1)若 的平分线交于点C.问:点B、A在OM、ON上运动过程中,∠C 的度数是否改变 若不改变,直接写出结论;若改变,说明理由.
(2)如图11-2-15所示,若∠ABO、∠BAN的平分线所在的直线相交于点C,其他条件不变,(1)中的结论是否成立 若成立,求出其值;若不成立,说明理由.
21.如图11-2-16所示,在△ADE和△ABC中,∠EAD=∠AED=∠BAC=∠BCA=45°,∠BAD=∠BCF.
(1)求∠ECF+∠DAC+∠ECA的度数;
(2)判断ED与FC 的位置关系,并对你的结论加以证明.
22.如图11-2-17(a)所示,在平面直角坐标系中,△DEQ的一个顶点在x轴的负半轴上,边DQ交x 轴于点C,且CE 平分∠DEQ,过点 D 作直线交x 轴于点 B,交 y 轴于点 A,使∠ADE=∠BDC,已知C(m,0),E(n,0),其中m,n满足|
(1)求点 C、E的坐标.
(2)若∠ABC=30°,求∠Q的度数.
(3)如图11-2-17(b)所示,在平面直角坐标系中,若直线AB绕点 D 旋转,过 D 作DH⊥AB,交x轴于点G,交y轴于点 H.直线AB绕点D 转动时,下列结论:①∠Q的大小不变; 的值不变.选择一个正确的结论,求其值,并证明你的结论.
23.将一副常规的三角尺按图11-2-18所示方式放置,则图中 的度数为( ).
A.75° B.95°
24.一副三角板叠在一起,按图11-2-19所示方式放置,最小锐角的顶点 D 恰好放在等腰直角三角板的斜边AB上,BC 与DE 交于点M.如果 ,那么. 的度数为 .
巅峰突破
25. 如图 11-2-20 所示, 在 中, 则射线 AF 与BG( ).
A.平行 B.延长后相交
C.反向延长后相交 D.可能平行也可能相交
如图 11-2-21所示,DC平分∠ADB,EC平分∠AEB,若 则∠C= .(用α、β表示)
基础演练
1. A; 2. A; 3. C 4.(1)40°,60°,80°;
(2)90°;(3)钝角
5.30°; 6.35°
7.如下图所示,过点G作GM∥BE,
∴∠1=∠E.
∵∠EGF=∠E+∠F=∠1+∠2,
∴∠F=∠2.∴BE∥MG∥FC.
∴∠BHP+∠CPH=180°.
∵∠BHD是△ABH的一个外角,
∴∠BHD=∠A+∠B.
同理可证:∠CPA=∠C+∠D.
∴∠A+∠B+∠C+∠D=180°.
8.(1)∵AE平分∠BAC,
∵∠BAC+∠B+∠C=180°,
∵AD⊥BC,∴∠DAC=90°-∠C.
(2)∠BID=∠HIC.
【理由】∵AD、BE、CF为△ABC的角平分线,
∵∠BID 是△ABI的一个外角,
∵IH⊥BC,∴∠IHC=90°.
∴∠BID=∠HIC.
能力提升
9. D; 10. C; 11. B; 12. B; 13.α=β+γ.
14.130°或50°. 15.70°或110°. 16.8°;2
18.如下图所示,延长 BA,可证 AG 平分∠CAH,利用模型(5)可得:
又可证: 进而求出∠ACB=60°.
19.(1)6个.
(2)由材料可得:∠A+∠ABE=∠E+∠EDG.①
∠E+∠EBC=∠C+∠CDE.②
①+②得:∠A+∠ABE+∠C+∠CDE=∠E+∠EDG+∠E+∠EBC.
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC,∠CDE=∠EDG.
∴∠A+∠C=2∠E.
∵∠A=48°,∠C=46°,∴∠E=47°,
(3)由(2)可得:∠A+∠C=2∠E.
20.(1)∠C的度数不会改变,且∠C=45°.
(2)成立.
∵∠DAB是∠CAB的一个外角,
∴∠DAB=∠C+∠CBA.
∴2∠DAB=2∠C+2∠CBA.
∵∠NAB是△AOB的一个外角,
∴∠NAB=∠O+∠ABO.
∵AD平分∠NAB,BC平分∠ABO,
∴∠NAB=2∠DAB,∠ABO=2∠CBA.
∴2∠DAB=∠O+2∠CBA
21.(1)∵∠ECF=∠ECB+∠BCF,∠BCF=∠BAD,
∴∠ECF=∠BAD+∠ECB.
∴∠ECF+∠DAC+∠ECA
=(∠ECB+∠BAD)+∠DAC+∠ECA
=(∠ECB+∠ECA)+(∠DAC+∠BAD)
=∠BCA+∠BAC.
∵∠BAC=∠BCA=45°,
∴∠ECF+∠DAC+∠ECA=90°.
(2)ED∥FC.理由如下:
如下图所示,延长AD、CF交于点G,由(1)可证:∠G=90°,
∵∠EAD=∠AED=45°,∴∠EDA=90°.
∴∠EDG=90°.
∴∠EDG=∠G.∴DE∥CF.
22.(1)C(3,0),E(-4,0)
(2)如下图所示,延长ED至点F,则∠ADE=∠BDF.
又∵∠ADE=∠BDC,∴∠BDF=∠BDC.
∵CE平分∠DEQ,∴∠DEB=∠QEB.
∴2∠BDF=2∠ABC+∠DEQ,
即∠FDQ=2∠ABC+∠DEQ.
∵∠FDQ=∠Q+∠DEQ,
∴∠Q=2∠ABC=2×30°=60°.
(3)②正确.
理由:在直线 AB 绕点 D 旋转的过程中,CE 仍平分∠DEQ,BD 仍是△EDQ的外角平分线,
由(2)可知:∠Q=2∠ABC.
∵DH⊥AB,∴∠HDB=∠HOG=90°.
∵∠OGH=∠DGB,∴∠OHD=∠ABC.
中考链接
23. C; 24.85°
巅峰突破
25. A; 26.α+β
