13.1轴对称与轴对称图形 培优训练(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 13.1轴对称与轴对称图形 培优训练(含答案)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 07:26:44 | ||
图片预览



文档简介
13.1轴对称与轴对称图形
一、课标导航
课标内容 课标要求 目标层次
轴对称 了解图形的轴对称,理解对应点所连的线段被对称轴垂直平分的性质 ★
了解物体的镜面对称 ★
能按要求作出简单平面图形经过一次或两次轴对称后的图形 ★★
掌握简单图形之间的轴对称关系,并能指出对称轴 ★★
掌握基本图形的轴对称性及其相关性质 ★★
能运用轴对称的知识解决简单问题 ★★★
二、核心纲要
1.线段的垂直平分线(中垂线)
(1)定义:经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线.
(2)性质:线段垂直平分线上的点到线段两个端点的距离相等.
(3)判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(4)画法:分别以线段AB两个端点为圆心,大于 长为半径画弧,两弧交于两点 C、D,作直线CD,则直线CD是线段AB 的垂直平分线(如右图所示).
2.轴对称
(1)轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形.这条直线是对称轴.
注:①轴对称图形指的是一个图形,它被对称轴分成的两部分互相重合;
②一个轴对称图形的对称轴不一定只有一条;
③对称轴是一条直线.
(2)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,就说这两个图形关于这条直线对称,这条直线是对称轴,折叠后重合的点是对应点,叫做对称点.
(3)轴对称、轴对称图形的性质
①关于某条直线对称的两个图形是全等形;
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上;
注:轴对称图形一定是全等形,全等的图形不一定成轴对称.
(4)轴对称作图
①画图形的对称轴:找出轴对称图形的任意一组对称点,连接对称点,得到一条线段,作这条线段的垂直平分线即可.
②画某点关于某直线的对称点
过已知点作已知直线(对称轴)的垂线,标出垂足,在这条直线的另一侧从垂足出发在垂线上截取与已知点到垂足的距离相等的线段,截点就是这点关于该直线的对称点.
③画已知图形关于某直线的对称图形
画出图形的某些特殊点关于这条直线的对称点,把这些对称点顺次连接起来,就形成了一个符合条件的对称图形.
(5)图形对称轴的作法:要作两个图形的对称轴,只要找到这两个图形的一对对应点,然后连接它们,得到一条线段,再作出这条线段的垂直平分线,这条垂直平分线就是这两个图形的对称轴.
3.常见的轴对称图形
(1)线段:两条对称轴,对称轴是线段的垂直平分线和线段本身所在直线.
(2)角:一条对称轴,对称轴是角平分线所在直线.
(3)圆:无数条对称轴,对称轴是经过圆心的直线.
(4)正方形:四条对称轴,对角线所在直线及对边中点连线所在直线.
(5)矩形:两条对称轴,对边中点连线所在直线.
(6)菱形:两条对称轴,对角线所在直线.
(7)等腰三角形:一条对称轴,底边中线(底边高线或顶角平分线)所在直线.
(8)等边三形:三条对称轴,三边中线(高线或内角平分线)所在直线.
本节重点讲解:两个性质(线段垂直平分线的性质,轴对称及轴对称图形的性质),三个定义(线段垂直平分线的定义,轴对称及轴对称图形).
三、全能突破
基础演练
1.图13-1-1所示的四个图案中,轴对称图形的个数是( ).
A.1 B.2 C.3 D.4
2.如图13-1-2 所示, 和 关于直线l 对称,下列结论中:(
=∠B'AC;③l垂直平分CC';④直线BC和B'C'的交点不一定在直线l上,正确的有( ).
A.4个 B.3个
C.2个 D.1 个
3.下列说法:①若直线 PE 是线段AB 的垂直平分线,则EA=EB,PA=PB;②若 PA=PB,EA=EB,则直线PE是线段AB 垂直平分线;③若PA=PB,EA=EB,则AB垂直平分PE;④若PA=PB,则点 P 必是线段AB 的垂直平分线上的点;⑤若EA=EB,则过点 E的直线垂直平分线段AB.其中正确的个数有( ).
A.1个 B.2个
C.3个 D.4 个
4.图13-1-3所示是某时刻在镜子中看到准确时钟的情况,则实际时间是
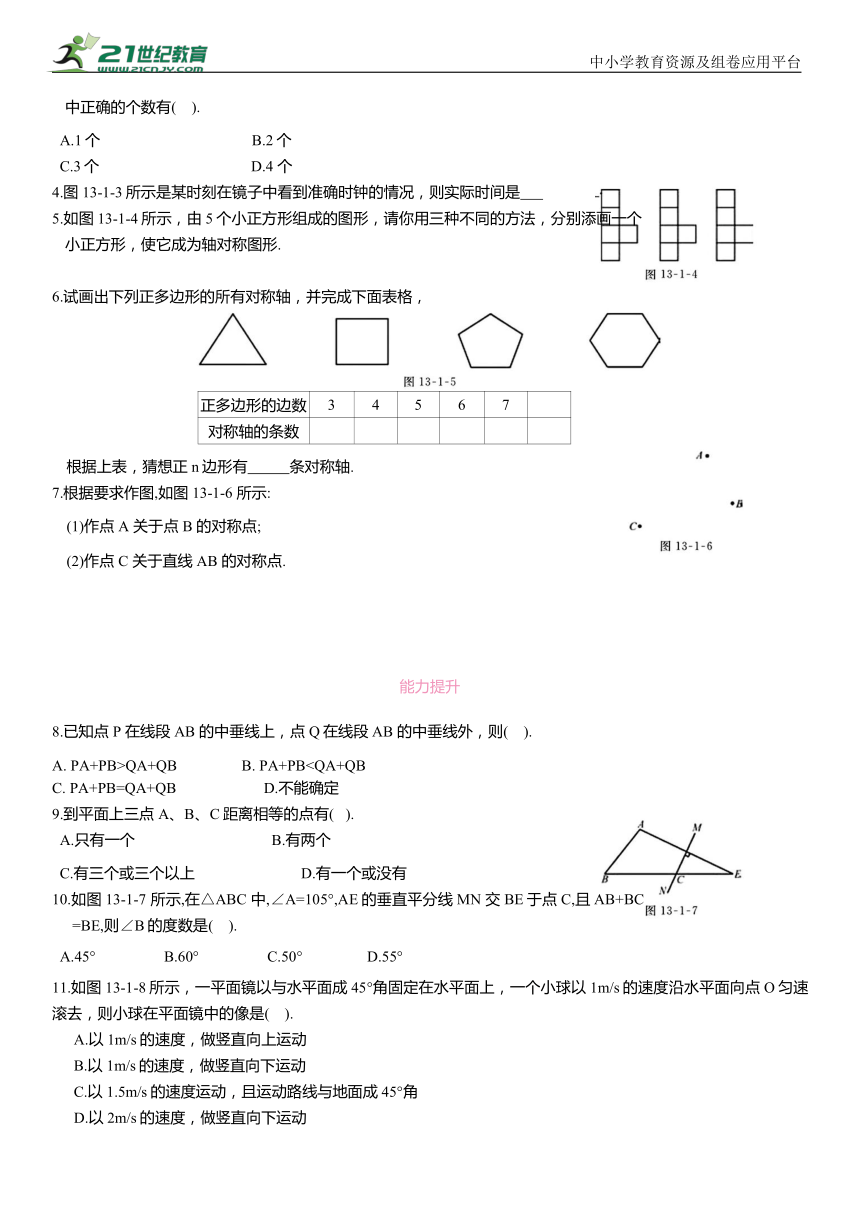
5.如图13-1-4所示,由5个小正方形组成的图形,请你用三种不同的方法,分别添画一个小正方形,使它成为轴对称图形.
6.试画出下列正多边形的所有对称轴,并完成下面表格,
正多边形的边数 3 4 5 6 7
对称轴的条数
根据上表,猜想正n边形有 条对称轴.
7.根据要求作图,如图13-1-6 所示:
(1)作点 A 关于点 B 的对称点;
(2)作点 C 关于直线AB 的对称点.
能力提升
8.已知点 P 在线段AB 的中垂线上,点Q在线段AB 的中垂线外,则( ).
A. PA+PB>QA+QB B. PA+PBC. PA+PB=QA+QB D.不能确定
9.到平面上三点 A、B、C距离相等的点有( ).
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
10.如图13-1-7 所示,在△ABC 中,∠A=105°,AE的垂直平分线MN 交BE于点C,且AB+BC=BE,则∠B的度数是( ).
A.45° B.60° C.50° D.55°
11.如图13-1-8所示,一平面镜以与水平面成45°角固定在水平面上,一个小球以1m/s的速度沿水平面向点 O匀速滚去,则小球在平面镜中的像是( ).
A.以1m/s的速度,做竖直向上运动
B.以1m/s的速度,做竖直向下运动
C.以1.5m/s的速度运动,且运动路线与地面成45°角
D.以2m/s的速度,做竖直向下运动
12.如图13-1-9 所示,D是线段AB、BC垂直平分线的交点,若∠ABC=150°,则∠ADC的大小是( ).
A.60° B.70° C.75° D.80°
13.在△ABC中,AB、AC的垂直平分线分别交BC 于点E、F,若∠BAC=115°,则∠EAF= .
14.如图13-1-10所示,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF 垂直平分AD,交 BC的延长线于 F,则∠CAF= .
15.图13-1-11 所示是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子放在棋盘内,沿着棋子对称跳行,跳行一次称为一步.已知点 A为一方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为 步.
16.小强用火柴棒在桌上摆了一个不正确的等式,如图13-1-12 所示,你有没有什么办法,在不移动火柴棒的情况下,使桌面出现一个正确的等式
图 13-1-12
17.(1)如图13-1-13 所示,已知∠AOB和C、D两点,求作一点 P,使 PC=PD,且 P 到∠AOB 两边的距离相等.
(2)有一张矩形纸片 ABCD,如图13-1-14 所示,上面画有一个角的两边 m、n,但是这个角的顶点 P在纸片的外部,试在纸片上作出∠P 的平分线来.
中小学教育资源及组卷应用平台
18.如图13-1-15 所示,在△ABC中,DE 是 AC 的垂直平分线, 的周长为 13cm,求△ABC的周长.
19.如图13-1-16所示,在△ABC中,AB>AC,AD⊥BC,垂足为点 D,P为AD 上任一点,求证:PB-PC>AB-AC.
20.如图13-1-17 所示,在不等边△ABC中,AB=2,AC=3,AB 的垂直平分线交BC 边于点E,AC的垂直平分线交 BC 边于点 N.
(1)若 BC边长为整数,则△AEN的周长为 .
(2)①若∠BAC=70°,则∠EAN的度数为 ;
②若∠BAC=100°,则∠EAN的度数为 ;
③若∠BAC≠90°,请直接写出∠BAC与∠EAN 之间的数量关系,并画出相应的图形.
21.如图13-1-18所示,AD∥BC,CD=2AD,过点 D 作DE∥AB,交∠BCD 的平分线于点E,连接 BE,延长 DE 交BC 于F,CD=2CF.
(1)求证:BC=CD.
(2)将△BCE绕点 C 顺时针旋转 90°得到△DCG,连接 EG.求证:CD 垂直平分 EG.
(3)延长BE 交CD 于点P,求证:P 是CD 的中点.
22.(1)如图13-1-19所示,在矩形ABCD中,AB=10,BC=5,点E、F 分别在AB、CD上,将矩形ABCD 沿EF 折叠,使点A、D分别落在长方形ABCD 外部的点 A 、D 处,则阴影部分图形的周长为( ).
A.15 B.20 C.25 D.30
(2))图13-1-20(a)所示的长方形 ABCD 中,E点在AD 上,且BE=2AE.分别以 BE、CE 为折线,将点 A、D向BC的方向折过去,图13-1-20(b)为对折后 A、B、C、D、E五点均在同一平面上的位置图.若图13-1-20(b)中, 则 的度数为何 ( )
A.30°
23.图13-1-21所示是一台球桌面示意图,图中小正方形的边长均相等,黑球放在图中所示位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.① B.②
C.⑤ D.⑥
巅峰突破
24.如果直线 l 、l 相交成30°的角,交点为O,P为平面上任意一点,若作点 P 关于l 的对称点 P 是第1次,再作点 P 关于l 的对称点 P 是第2次,以后继续轮流作关于 l 、l 的对称点.那么经过 次后,能回到点 P.
25.如图13-1-22所示,在2×2的正方形格纸中,有一个以格点为顶点的 ,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有 个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
26.某台球桌面为图 13-1-23 所示的长方形ABCD,小球从 A 沿 角击出,恰好经过5次碰撞到 B处,则.
A.1 : 2 B.2: 3
C.2:5 D.3:5
基础演练
1. C; 2. B; 3. C; 4.4点40分
5.图略;6.3,4,5,6,7;n;7.图略
能力提升
8. D; 9. D; 10. C; 11. B; 12. A;
13.50°; 14.45°; 15.3
16.沿着镜面反射即可,如下图所示.152-20=132
17.(1)如下图所示,点P是角平分线与垂直平分线的交点.
(2)作法:如下图所示,①在矩形内部作直线h⊥m,作n关于h 的对称直线EP'交m 于P',
②作∠P'的角平分线 P'F;
③作 P'F 关于直线h 的对称直线 FG.
FG 所在直线就是∠P 的平分线所在直线.
18.19cm
19.如下图所示,作C点关于AD的对称点 F,连接AF、PF
∴PC=PF,AC=AF.
∵AF+PB>PF+AB
∴AC+PB>AB+PC
∴PB-PC>AB-AC.
20.(1)4
(2)①40°; ②20°;
③如下图所示,若∠BAC 为钝 B角,则∠EAN=2∠BAC-180°;若∠BAC为锐角,则∠EAN
21.(1)如下图所示,连接BD.
∵AD∥BC,AB∥DF,
∴∠ABD=∠BDF,∠ADB=∠DBF,
∵BD=DB,∴△BAD≌△FDB,
∴AD=BF.∵CD=2AD,∴CD=2BF.
∵CD=2CF∴BF=CF.
即 BC=CD.
(2)∵CE平分∠BCD,∴∠BCE=∠DCE.
由(1)知 BC=CD,
∵CE=CE,∴△BCE≌△DCE.∴BE=DE.由图形旋转的性质知CE=CG,BE=DG,
∴DE=DG.∴C、D都在 EG的垂直平分线上,
∴CD 垂直平分 EG.
(3)由(2)知BE=DE,∴∠DBE=∠BDE.
∵AB∥DE.∴∠ABD=∠BDE.
∴∠DBE=∠ABD.
∵AD∥BC,∴∠ADB=∠DBC.
由(1)知BC=CD.∴∠DBC=∠BDC,
∴∠ADB=∠BDP.
又∵BD=BD,∴△BAD≌△BPD.
∴DP=AD.
∴P是CD 的中点.
中考链接
22.(1)D;(2)D. 23. A
巅峰突破
24.12
25.5,如下图所示:
26. C
一、课标导航
课标内容 课标要求 目标层次
轴对称 了解图形的轴对称,理解对应点所连的线段被对称轴垂直平分的性质 ★
了解物体的镜面对称 ★
能按要求作出简单平面图形经过一次或两次轴对称后的图形 ★★
掌握简单图形之间的轴对称关系,并能指出对称轴 ★★
掌握基本图形的轴对称性及其相关性质 ★★
能运用轴对称的知识解决简单问题 ★★★
二、核心纲要
1.线段的垂直平分线(中垂线)
(1)定义:经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线.
(2)性质:线段垂直平分线上的点到线段两个端点的距离相等.
(3)判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(4)画法:分别以线段AB两个端点为圆心,大于 长为半径画弧,两弧交于两点 C、D,作直线CD,则直线CD是线段AB 的垂直平分线(如右图所示).
2.轴对称
(1)轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形.这条直线是对称轴.
注:①轴对称图形指的是一个图形,它被对称轴分成的两部分互相重合;
②一个轴对称图形的对称轴不一定只有一条;
③对称轴是一条直线.
(2)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,就说这两个图形关于这条直线对称,这条直线是对称轴,折叠后重合的点是对应点,叫做对称点.
(3)轴对称、轴对称图形的性质
①关于某条直线对称的两个图形是全等形;
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上;
注:轴对称图形一定是全等形,全等的图形不一定成轴对称.
(4)轴对称作图
①画图形的对称轴:找出轴对称图形的任意一组对称点,连接对称点,得到一条线段,作这条线段的垂直平分线即可.
②画某点关于某直线的对称点
过已知点作已知直线(对称轴)的垂线,标出垂足,在这条直线的另一侧从垂足出发在垂线上截取与已知点到垂足的距离相等的线段,截点就是这点关于该直线的对称点.
③画已知图形关于某直线的对称图形
画出图形的某些特殊点关于这条直线的对称点,把这些对称点顺次连接起来,就形成了一个符合条件的对称图形.
(5)图形对称轴的作法:要作两个图形的对称轴,只要找到这两个图形的一对对应点,然后连接它们,得到一条线段,再作出这条线段的垂直平分线,这条垂直平分线就是这两个图形的对称轴.
3.常见的轴对称图形
(1)线段:两条对称轴,对称轴是线段的垂直平分线和线段本身所在直线.
(2)角:一条对称轴,对称轴是角平分线所在直线.
(3)圆:无数条对称轴,对称轴是经过圆心的直线.
(4)正方形:四条对称轴,对角线所在直线及对边中点连线所在直线.
(5)矩形:两条对称轴,对边中点连线所在直线.
(6)菱形:两条对称轴,对角线所在直线.
(7)等腰三角形:一条对称轴,底边中线(底边高线或顶角平分线)所在直线.
(8)等边三形:三条对称轴,三边中线(高线或内角平分线)所在直线.
本节重点讲解:两个性质(线段垂直平分线的性质,轴对称及轴对称图形的性质),三个定义(线段垂直平分线的定义,轴对称及轴对称图形).
三、全能突破
基础演练
1.图13-1-1所示的四个图案中,轴对称图形的个数是( ).
A.1 B.2 C.3 D.4
2.如图13-1-2 所示, 和 关于直线l 对称,下列结论中:(
=∠B'AC;③l垂直平分CC';④直线BC和B'C'的交点不一定在直线l上,正确的有( ).
A.4个 B.3个
C.2个 D.1 个
3.下列说法:①若直线 PE 是线段AB 的垂直平分线,则EA=EB,PA=PB;②若 PA=PB,EA=EB,则直线PE是线段AB 垂直平分线;③若PA=PB,EA=EB,则AB垂直平分PE;④若PA=PB,则点 P 必是线段AB 的垂直平分线上的点;⑤若EA=EB,则过点 E的直线垂直平分线段AB.其中正确的个数有( ).
A.1个 B.2个
C.3个 D.4 个
4.图13-1-3所示是某时刻在镜子中看到准确时钟的情况,则实际时间是
5.如图13-1-4所示,由5个小正方形组成的图形,请你用三种不同的方法,分别添画一个小正方形,使它成为轴对称图形.
6.试画出下列正多边形的所有对称轴,并完成下面表格,
正多边形的边数 3 4 5 6 7
对称轴的条数
根据上表,猜想正n边形有 条对称轴.
7.根据要求作图,如图13-1-6 所示:
(1)作点 A 关于点 B 的对称点;
(2)作点 C 关于直线AB 的对称点.
能力提升
8.已知点 P 在线段AB 的中垂线上,点Q在线段AB 的中垂线外,则( ).
A. PA+PB>QA+QB B. PA+PB
9.到平面上三点 A、B、C距离相等的点有( ).
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
10.如图13-1-7 所示,在△ABC 中,∠A=105°,AE的垂直平分线MN 交BE于点C,且AB+BC=BE,则∠B的度数是( ).
A.45° B.60° C.50° D.55°
11.如图13-1-8所示,一平面镜以与水平面成45°角固定在水平面上,一个小球以1m/s的速度沿水平面向点 O匀速滚去,则小球在平面镜中的像是( ).
A.以1m/s的速度,做竖直向上运动
B.以1m/s的速度,做竖直向下运动
C.以1.5m/s的速度运动,且运动路线与地面成45°角
D.以2m/s的速度,做竖直向下运动
12.如图13-1-9 所示,D是线段AB、BC垂直平分线的交点,若∠ABC=150°,则∠ADC的大小是( ).
A.60° B.70° C.75° D.80°
13.在△ABC中,AB、AC的垂直平分线分别交BC 于点E、F,若∠BAC=115°,则∠EAF= .
14.如图13-1-10所示,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF 垂直平分AD,交 BC的延长线于 F,则∠CAF= .
15.图13-1-11 所示是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子放在棋盘内,沿着棋子对称跳行,跳行一次称为一步.已知点 A为一方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为 步.
16.小强用火柴棒在桌上摆了一个不正确的等式,如图13-1-12 所示,你有没有什么办法,在不移动火柴棒的情况下,使桌面出现一个正确的等式
图 13-1-12
17.(1)如图13-1-13 所示,已知∠AOB和C、D两点,求作一点 P,使 PC=PD,且 P 到∠AOB 两边的距离相等.
(2)有一张矩形纸片 ABCD,如图13-1-14 所示,上面画有一个角的两边 m、n,但是这个角的顶点 P在纸片的外部,试在纸片上作出∠P 的平分线来.
中小学教育资源及组卷应用平台
18.如图13-1-15 所示,在△ABC中,DE 是 AC 的垂直平分线, 的周长为 13cm,求△ABC的周长.
19.如图13-1-16所示,在△ABC中,AB>AC,AD⊥BC,垂足为点 D,P为AD 上任一点,求证:PB-PC>AB-AC.
20.如图13-1-17 所示,在不等边△ABC中,AB=2,AC=3,AB 的垂直平分线交BC 边于点E,AC的垂直平分线交 BC 边于点 N.
(1)若 BC边长为整数,则△AEN的周长为 .
(2)①若∠BAC=70°,则∠EAN的度数为 ;
②若∠BAC=100°,则∠EAN的度数为 ;
③若∠BAC≠90°,请直接写出∠BAC与∠EAN 之间的数量关系,并画出相应的图形.
21.如图13-1-18所示,AD∥BC,CD=2AD,过点 D 作DE∥AB,交∠BCD 的平分线于点E,连接 BE,延长 DE 交BC 于F,CD=2CF.
(1)求证:BC=CD.
(2)将△BCE绕点 C 顺时针旋转 90°得到△DCG,连接 EG.求证:CD 垂直平分 EG.
(3)延长BE 交CD 于点P,求证:P 是CD 的中点.
22.(1)如图13-1-19所示,在矩形ABCD中,AB=10,BC=5,点E、F 分别在AB、CD上,将矩形ABCD 沿EF 折叠,使点A、D分别落在长方形ABCD 外部的点 A 、D 处,则阴影部分图形的周长为( ).
A.15 B.20 C.25 D.30
(2))图13-1-20(a)所示的长方形 ABCD 中,E点在AD 上,且BE=2AE.分别以 BE、CE 为折线,将点 A、D向BC的方向折过去,图13-1-20(b)为对折后 A、B、C、D、E五点均在同一平面上的位置图.若图13-1-20(b)中, 则 的度数为何 ( )
A.30°
23.图13-1-21所示是一台球桌面示意图,图中小正方形的边长均相等,黑球放在图中所示位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.① B.②
C.⑤ D.⑥
巅峰突破
24.如果直线 l 、l 相交成30°的角,交点为O,P为平面上任意一点,若作点 P 关于l 的对称点 P 是第1次,再作点 P 关于l 的对称点 P 是第2次,以后继续轮流作关于 l 、l 的对称点.那么经过 次后,能回到点 P.
25.如图13-1-22所示,在2×2的正方形格纸中,有一个以格点为顶点的 ,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有 个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
26.某台球桌面为图 13-1-23 所示的长方形ABCD,小球从 A 沿 角击出,恰好经过5次碰撞到 B处,则.
A.1 : 2 B.2: 3
C.2:5 D.3:5
基础演练
1. C; 2. B; 3. C; 4.4点40分
5.图略;6.3,4,5,6,7;n;7.图略
能力提升
8. D; 9. D; 10. C; 11. B; 12. A;
13.50°; 14.45°; 15.3
16.沿着镜面反射即可,如下图所示.152-20=132
17.(1)如下图所示,点P是角平分线与垂直平分线的交点.
(2)作法:如下图所示,①在矩形内部作直线h⊥m,作n关于h 的对称直线EP'交m 于P',
②作∠P'的角平分线 P'F;
③作 P'F 关于直线h 的对称直线 FG.
FG 所在直线就是∠P 的平分线所在直线.
18.19cm
19.如下图所示,作C点关于AD的对称点 F,连接AF、PF
∴PC=PF,AC=AF.
∵AF+PB>PF+AB
∴AC+PB>AB+PC
∴PB-PC>AB-AC.
20.(1)4
(2)①40°; ②20°;
③如下图所示,若∠BAC 为钝 B角,则∠EAN=2∠BAC-180°;若∠BAC为锐角,则∠EAN
21.(1)如下图所示,连接BD.
∵AD∥BC,AB∥DF,
∴∠ABD=∠BDF,∠ADB=∠DBF,
∵BD=DB,∴△BAD≌△FDB,
∴AD=BF.∵CD=2AD,∴CD=2BF.
∵CD=2CF∴BF=CF.
即 BC=CD.
(2)∵CE平分∠BCD,∴∠BCE=∠DCE.
由(1)知 BC=CD,
∵CE=CE,∴△BCE≌△DCE.∴BE=DE.由图形旋转的性质知CE=CG,BE=DG,
∴DE=DG.∴C、D都在 EG的垂直平分线上,
∴CD 垂直平分 EG.
(3)由(2)知BE=DE,∴∠DBE=∠BDE.
∵AB∥DE.∴∠ABD=∠BDE.
∴∠DBE=∠ABD.
∵AD∥BC,∴∠ADB=∠DBC.
由(1)知BC=CD.∴∠DBC=∠BDC,
∴∠ADB=∠BDP.
又∵BD=BD,∴△BAD≌△BPD.
∴DP=AD.
∴P是CD 的中点.
中考链接
22.(1)D;(2)D. 23. A
巅峰突破
24.12
25.5,如下图所示:
26. C
