13.3 等腰三角形 培优训练(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 13.3 等腰三角形 培优训练(含答案)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览




文档简介
13.3 等腰三角形
一、课标导航
课标内容 课标要求 目标层次
等腰三角形 了解等腰三角形、等边三角形、直角三角形的概念,会识别这三种图形 ★
理解等腰三角形、等边三角形、直角三角形的性质和判定 ★
能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题 ★★
会运用等腰三角形、等边三角形、直角三角形的知识解决相关问题 ★★★
二、核心纲要
1.等腰三角形
(1)定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
(2)性质
①两腰相等.②两底角相等(简称为等边对等角).
③等腰三角形顶角平分线、底边上的中线、底边上的高线互相重合(简称为“三线合一”).
④等腰三角形是轴对称图形,其顶角平分线、底边上的中线、底边上的高线所在直线是对称轴.
注:若AB=AC,则∠B=∠C,AD是. 的中线、角平分线、高线.
证明题目中的写法:
①已知高线
②已知中线
∵AB=AC,BD=CD,∴AD⊥BC,∠BAD=∠CAD.
③已知角平分线
∵AB=AC,∠BAD=∠CAD,∴AD⊥BC,BD=CD.
(3)判定
①有两条边相等的三角形是等腰三角形.
②有两个角相等的三角形是等腰三角形(简称“等角对等边”).
2.等边三角形
(1)定义:有三条边相等的三角形叫做等边三角形.
(2)性质:三边都相等,三个角都相等,每一个角都等于
(3)判定
①三条边都相等的三角形是等边三角形;②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
3.直角三角形
中小学教育资源及组卷应用平台
(1)定义:有一个角是直角的三角形是直角三角形.
(2)性质
①有一个角是 ;②两锐角互余;③如果一个锐角等于 ,那么它所对的直角边等于斜边的一半.
(3)判定:有一个角是直角的三角形是直角三角形.
4.等腰直角三角形
(1)定义:顶角为 的等腰三角形叫做等腰直角三角形.
(2)性质
①顶角等于 底角等于 ;②两直角边相等;③轴对称图形;④三线合一.
(3)判定
①顶角为( 的等腰三角形.②底角为 的等腰三角形.
5.等腰三角形的构造
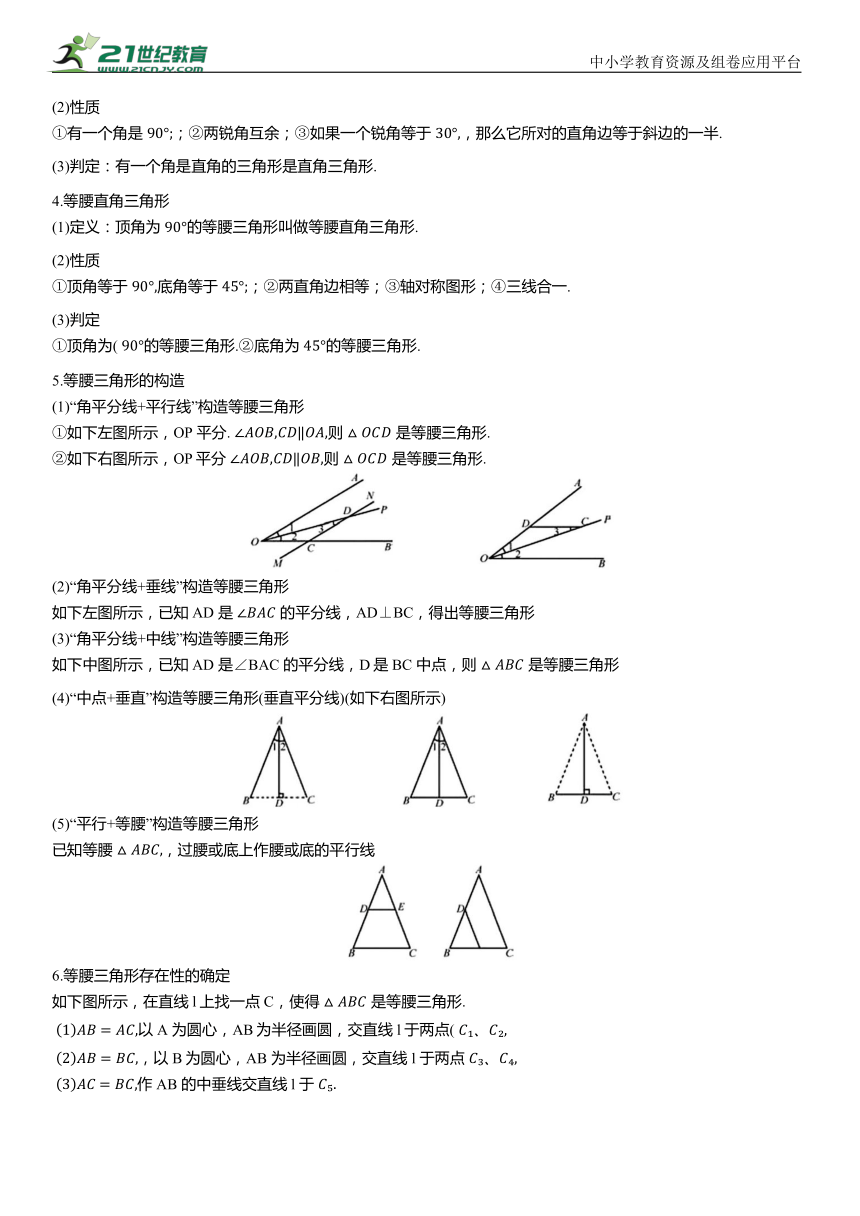
(1)“角平分线+平行线”构造等腰三角形
①如下左图所示,OP 平分. 则 是等腰三角形.
②如下右图所示,OP平分 则 是等腰三角形.
(2)“角平分线+垂线”构造等腰三角形
如下左图所示,已知AD 是 的平分线,AD⊥BC,得出等腰三角形
(3)“角平分线+中线”构造等腰三角形
如下中图所示,已知AD 是∠BAC 的平分线,D是BC 中点,则 是等腰三角形
(4)“中点+垂直”构造等腰三角形(垂直平分线)(如下右图所示)
(5)“平行+等腰”构造等腰三角形
已知等腰 ,过腰或底上作腰或底的平行线
6.等腰三角形存在性的确定
如下图所示,在直线l上找一点C,使得 是等腰三角形.
以 A 为圆心,AB为半径画圆,交直线 l于两点(
,以B为圆心,AB 为半径画圆,交直线 l 于两点
作 AB 的中垂线交直线l 于
本节重点讲解:一个构造,一个确定,四个概念、性质和判定.
三、全能突破
基础演练
1.等腰三角形是轴对称图形,它的对称轴是( ).
A.过顶点的直线 B.底边上的高
C.底边的中线 D.顶角平分线所在的直线
2.等腰三角形的一个内角是50°,则另外两个角的度数分别为( ).
A.65°,65° B.50°,80° C.65°,65°或50°,80° D.50°,50°
3.(1)要使得△ABC是等腰三角形,则需要满足下列条件中的( ).
A.∠A=50°,∠B=60° B.∠A=50°,∠B=100°
C.∠A+∠B=90°
(2)下列条件能证明△ABC为等腰三角形的是( )
①AD⊥BC,且AD平分BC;②AD⊥BC 于点 D,且∠BAD=∠CAD;③AD平分BC 边于点 D,且AD平分∠BAC.
A.只有① B.只有② C.只有③ D.①②③均可
(3)如图13-2-1所示,在△ABC中,D、E分别是AC、AB上的点,BD 与CE 相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( ).
A.2种 B.3种 C.4种 D.6种
4.等腰三角形顶角为30°,腰长是4cm,则三角形的面积为 .
5.(1)已知∠AOB=30°,点 P在OA 上,且OP=2,点 P 关于直线OB 的对称点是Q,则.
(2)已知∠AOB=30°,点 P在∠AOB 的内部,OP=3,点 P 和点 P 关于OA 对称,点 P 和点 P 关于OB 对称,则P 、O、P 三点构成的三角形是 三角形,其周长为 .
6.(1)如图13-2-2所示,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点 E作 交 AB于点M,交 AC于点 N,若BM+CN=9,则线段MN的长为 .
(2)如图13-2-3所示,已知 BC=3,∠ABC 和∠ACB的平分线相交于点O,( ,则△OEF 的周长为 .
7.如图13-2-4所示,AB=AC=4cm,DB=DC,若∠ABC为( ,则 BE 的长为 .
8.如图13-2-5 所示,在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,求∠CDE的度数.
能力提升
9.如图13-2-6所示,C 为线段AE 上一动点(不与点 A、E重合),在 AE 同侧分别作正三角形 ABC 和正三角形CDE,AD与BE 交于点O,AD与BC 交于点 P,BE与CD 交于点Q,连接PQ,下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是( )
A.①②③④ B.②③④⑤ C.①③④⑤ D.①②③⑤
10.连接正五边形A 、A 、A 、A 、A ,对角线交出一个正五边形 B B B B B .则以图13-2-7 中线段为边的三角形中,共有等腰三角形( )个.
A.25 B.30 C.35 D.40
11.如图13-2-8所示,在等边三角形ABC中,BD=CE,AD与BE 相交于点 P,则∠APE的度数是( ).
A.45° B.55° C.60° D.75°
12.(1)如图13-2-9所示,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,则符合条件的点C 有( )个.
A.3 B.5 C.8 D.10
(2)等边△ABC,在平面内找一点 P,使△PBC、△PAB、△PAC均为等腰三角形,具备这样条件的 P点有( )个.
A.1 个 B.4 个 C.7 个 D.10 个
13.(1)如图13-2-10所示,四边形ABCD中,AB=BD=DA=AC,则四边形 ABCD中,最大的内角的度数是( ).
A.90° B.120° C.135° D.150°
(2)如图13-2-11 所示,已知O是四边形ABCD 内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( ).
A.70° B.110°
14.(1)等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的底边长为 .
(2)已知等腰三角形的两条边为10、16,那么它的周长等于 .
15.(1)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为 .
(2)已知△ABC的周长为24,AB=AC,AD⊥BC于点D,若△ABD的周长为20,则AD的长为 .
(3)已知等腰三角形的周长为24,腰长为x,则x的取值范围是 .
16.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为 .
17.如图13-2-12 所示,在△ABC 中,AB=AC,AD 是BC 边上的高,点 E、F 是AD 的三等分点,若△ABC的面积为12cm ,则图中阴影部分的面积为 cm .
18.如图13-2-13所示,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF 交AC 于点E,交 BC 于点F.求证:BF=2CF.
19.如图13-2-14所示,在△ABC中,AB=AC,AD=AE.求证:BD=CE.
20.如图13-2-15 所示,已知△ABC 是等腰直角三角形, BE 是 的平分线,DE⊥BC,垂足为 D.
(1)请你写出图中所有的等腰三角形.
(2)请你判断AD 与BE 垂直吗 并说明理由.
(3)如果 BC=10,求AB+AE的长.
21.两个全等的含 角的三角板 ADE 和三角板ABC 按图13-2-16 所示方式放置,E、A、C 三点在一条直线上,连接 BD,取 BD 的中点M,连接 ME、MC.试判断 的形状,并说明理由.
22.如图13-2-17 所示,在△ABC 中, ,BE 平分. 于点D,且AF⊥BC于点 F,交 BE 于点 H.
(1)求证:
(2)探究 BH 与CD 的大小关系,并证明.
23.(1)如图13-2-18所示,在Rt△ABC中,∠ACB=90°,AB 的垂直平分线DE 交于 BC的延长线于点 F,若∠F=30°,DE=1,则 EF 的长是( ).
A.3 B.2 C D.1
(2)如图 13-2-19 所示,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若 EC=1,则EF= .
24.如图13-2-20所示,△ABC是等边三角形,D是AB 边上的一点,以 CD 为边作等边三角形CDE,使点 E、A 在直线DC 的同侧,连接AE.求证:AE∥BC.
巅峰突破
25.如图13-2-21所示,过边长为3的等边三角形ABC的边AB 上一点P,作PE⊥AC 于点E,Q为BC 延长线上一点,当PA=CQ时,连接PQ 交边AC 于点D,则 DE 的长为 .
26.数学课上,李老师出示了如下框中的题目.
在等边三角形 ABC 中,点 E 在AB上,点 D 在CB的延长线上,且ED=EC,如图 13-2-22 所示.试确定线段 AE 与DB 的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况·探索结论
当点 E 为 AB 的中点时,如图 13-2-23(a)所示,确定线段 AE 与 DB 的大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).
(2)特例启发,解答題目
解:题目中,AE与DB 的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图13-2-23(b)所示,过点E作EF∥BC,交 AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点 D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求 CD的长(请你直接写出结果).
27.(1)操作发现:如图 13-2-24(a)所示,D 是等边三角形 ABC 边 BA 上一动点(点 D 与点 B 不重合),连接 DC,以 DC 为边在BC 上方作等边三角形DCF,连接AF.你能发现线段 AF 与BD之间的数量关系吗 并证明你发现的结论.
(2)类比猜想:如图13-2-24(b)所示,当动点 D运动至等边三角形ABC 边BA 的延长线上时,其他作法与(1)相同,猜想AF 与BD 在(1)中的结论是否仍然成立 (直接写出结论)
(3)深入探究
①如图 13-2-24(c)所示,当动点 D 在等边三角形ABC 边BA 上运动时(点 D 与点 B 不重合)连接DC,以 DC 为边在BC 上方、下方分别作等边三角形 DCF 和等边三角形DCF',连接AF、BF',探究 AF、BF'与AB 有何数量关系 并证明你探究的结论.
②如图13-2-24(d)所示,当动点 D 在等边三角形边BA 的延长线上运动时,其他作法与图13-2-24(c)相同,①中的结论是否成立 若不成立,是否有新的结论 并证明你得出的结论.
基础演练
1. D; 2. C; 3.(1)D;(2)D;(3)C
4.4 5.(1)2;(2)等边;9
6.(1)9;(2)3 7.2cm
8.∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
∵∠BAD=40°,∴∠CAD=40°.
∵AD=AE,∴∠ADE=∠AED.
∵∠ADE+∠AED+∠CAD=180°.
∴∠ADE=70°.∵∠ADC=90°,∴∠CDE=20°.
能力提升
9. D;10. C;11. C;12.(1)C;(2)D
13.(1)D;(2)D 14.(1)3cm;(2)42或36
15.(1)4cm或8cm;(2)8;(3)616.30°或150° 17.6
18.连接AF,
∵AB=AC,∠BAC=120°,AC的垂直平分线EF 交AC于点E,∴∠B=∠C=30°,AF=CF.
∴∠C=∠FAC=30°,∠BAF=90°.
∴BF=2AF=2CF.
19.过点A作AF⊥BC,垂足为点 F,
∵AB=AC,AF⊥BC,∴BF=CF.
∵AD=AE,AF⊥BC,∴DF=EF.
∴BF-DF=CF-EF.即 BD=CE.
20.(1)△ABD、△AED、△ABC、△DEC.
(2)垂直
证明:∵△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,
∴AE=DE,AB=AC
∵AE=DE,BE=BE.
∴Rt△ABE≌Rt△DBE.
∴AB=BD,∴AD⊥BE.
(3)AB+AE=BD+DE=BD+DC=BC=10.
21.连接MA,
∵∠EAD=30°,∠BAC=60°,∴∠DAB=90°,
∵△EDA≌△CAB,∴DA=AB,ED=AC.
∴△DAB是等腰直角三角形,又 M为BD的中点,
∴∠MDA=∠MBA=45°,AM⊥BD.
∴△DAM与△MAB是等腰直角三角形.
∴AM BD=MD.∴∠EDM=∠MAC=105°
∵ED=AC,∠MDE=∠MAC,MD=AM,
∴△MDE≌△MAC.
∴∠DME=∠AMC,ME=MC,
又∵∠DMA=90°,
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°.
∴△EMC是等腰直角三角形.
22.(1)延长 BA交CD 延长线于点M.
∵∠MBD=∠CBD,BD⊥CD,BD=BD,
∴△BCD≌△BMD.∴CD=DM CM
∵∠MCA+∠M=90°,∠DBA+∠M=90°,
∴∠MCA=∠DBA.
又∵AC=AB,∠MAC=∠EAB=90°,
∴△MCA≌△EBA.∴CM=BE.
∵CM=2CD,∴BE=2CD.即
(2)连接CH,Rt△CDH中,CH>CD,BH=CH,∴BH>CD.
中考链接
23.(1)B;(2)2
24.∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠ABC=∠BCA=∠ECD=60°,
∴∠BCA-∠DCA=∠ECD-∠DCA.
即∠BCD=∠ACE,∴△ACE≌△BCD.
∴∠EAC=∠DBC=60°=∠ACB.∴AE∥BC.
巅峰突破
25
26.(1)=.(2)=.
证明:在等边△ABC中,
∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,∴∠AEF=∠AFE=60°=∠BAC,
∴AE=AF=EF.
∴AB-AE=AC-AF.即BE=CF.
∵∠ABC=∠EDB+∠BED=60°,∠ACB=∠ECB+∠FCE=60°,
∵ED=EC,∴∠EDB=∠ECB.
∴∠BED=∠FCE.
∵EB=FC,∴△DBE≌△EFC.
∴DB=EF.∴AE=BD.
(3)如下图所示:
27.(1)AF=BD;
证明如下:∵△ABC是等边三角形,
∴BC=AC,∠BCA=60°;
同理可得:DC=CF,∠DCF=60°;
∴∠BCA-∠DCA=∠DCF-∠DCA.
即∠BCD=∠ACF.
∴△BCD≌△ACF.∴BD=AF.
(2)AF=BD.
证明:由(1)知,△BCD≌△ACF.∴BD=AF.
同理△BCF'≌△ACD.
② ①中的结论不成立.新的结论是AF=AB+BF';
∵BC=AC,∠BCF'=∠ACD,F'C=DC,
∴△BCF'≌△ACD.∴BF'=AD.
又由(2)知,AF=BD.
∴AF=BD=AB+AD=AB+BF'.
即AF=AB+BF'.
一、课标导航
课标内容 课标要求 目标层次
等腰三角形 了解等腰三角形、等边三角形、直角三角形的概念,会识别这三种图形 ★
理解等腰三角形、等边三角形、直角三角形的性质和判定 ★
能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题 ★★
会运用等腰三角形、等边三角形、直角三角形的知识解决相关问题 ★★★
二、核心纲要
1.等腰三角形
(1)定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
(2)性质
①两腰相等.②两底角相等(简称为等边对等角).
③等腰三角形顶角平分线、底边上的中线、底边上的高线互相重合(简称为“三线合一”).
④等腰三角形是轴对称图形,其顶角平分线、底边上的中线、底边上的高线所在直线是对称轴.
注:若AB=AC,则∠B=∠C,AD是. 的中线、角平分线、高线.
证明题目中的写法:
①已知高线
②已知中线
∵AB=AC,BD=CD,∴AD⊥BC,∠BAD=∠CAD.
③已知角平分线
∵AB=AC,∠BAD=∠CAD,∴AD⊥BC,BD=CD.
(3)判定
①有两条边相等的三角形是等腰三角形.
②有两个角相等的三角形是等腰三角形(简称“等角对等边”).
2.等边三角形
(1)定义:有三条边相等的三角形叫做等边三角形.
(2)性质:三边都相等,三个角都相等,每一个角都等于
(3)判定
①三条边都相等的三角形是等边三角形;②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
3.直角三角形
中小学教育资源及组卷应用平台
(1)定义:有一个角是直角的三角形是直角三角形.
(2)性质
①有一个角是 ;②两锐角互余;③如果一个锐角等于 ,那么它所对的直角边等于斜边的一半.
(3)判定:有一个角是直角的三角形是直角三角形.
4.等腰直角三角形
(1)定义:顶角为 的等腰三角形叫做等腰直角三角形.
(2)性质
①顶角等于 底角等于 ;②两直角边相等;③轴对称图形;④三线合一.
(3)判定
①顶角为( 的等腰三角形.②底角为 的等腰三角形.
5.等腰三角形的构造
(1)“角平分线+平行线”构造等腰三角形
①如下左图所示,OP 平分. 则 是等腰三角形.
②如下右图所示,OP平分 则 是等腰三角形.
(2)“角平分线+垂线”构造等腰三角形
如下左图所示,已知AD 是 的平分线,AD⊥BC,得出等腰三角形
(3)“角平分线+中线”构造等腰三角形
如下中图所示,已知AD 是∠BAC 的平分线,D是BC 中点,则 是等腰三角形
(4)“中点+垂直”构造等腰三角形(垂直平分线)(如下右图所示)
(5)“平行+等腰”构造等腰三角形
已知等腰 ,过腰或底上作腰或底的平行线
6.等腰三角形存在性的确定
如下图所示,在直线l上找一点C,使得 是等腰三角形.
以 A 为圆心,AB为半径画圆,交直线 l于两点(
,以B为圆心,AB 为半径画圆,交直线 l 于两点
作 AB 的中垂线交直线l 于
本节重点讲解:一个构造,一个确定,四个概念、性质和判定.
三、全能突破
基础演练
1.等腰三角形是轴对称图形,它的对称轴是( ).
A.过顶点的直线 B.底边上的高
C.底边的中线 D.顶角平分线所在的直线
2.等腰三角形的一个内角是50°,则另外两个角的度数分别为( ).
A.65°,65° B.50°,80° C.65°,65°或50°,80° D.50°,50°
3.(1)要使得△ABC是等腰三角形,则需要满足下列条件中的( ).
A.∠A=50°,∠B=60° B.∠A=50°,∠B=100°
C.∠A+∠B=90°
(2)下列条件能证明△ABC为等腰三角形的是( )
①AD⊥BC,且AD平分BC;②AD⊥BC 于点 D,且∠BAD=∠CAD;③AD平分BC 边于点 D,且AD平分∠BAC.
A.只有① B.只有② C.只有③ D.①②③均可
(3)如图13-2-1所示,在△ABC中,D、E分别是AC、AB上的点,BD 与CE 相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( ).
A.2种 B.3种 C.4种 D.6种
4.等腰三角形顶角为30°,腰长是4cm,则三角形的面积为 .
5.(1)已知∠AOB=30°,点 P在OA 上,且OP=2,点 P 关于直线OB 的对称点是Q,则.
(2)已知∠AOB=30°,点 P在∠AOB 的内部,OP=3,点 P 和点 P 关于OA 对称,点 P 和点 P 关于OB 对称,则P 、O、P 三点构成的三角形是 三角形,其周长为 .
6.(1)如图13-2-2所示,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点 E作 交 AB于点M,交 AC于点 N,若BM+CN=9,则线段MN的长为 .
(2)如图13-2-3所示,已知 BC=3,∠ABC 和∠ACB的平分线相交于点O,( ,则△OEF 的周长为 .
7.如图13-2-4所示,AB=AC=4cm,DB=DC,若∠ABC为( ,则 BE 的长为 .
8.如图13-2-5 所示,在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,求∠CDE的度数.
能力提升
9.如图13-2-6所示,C 为线段AE 上一动点(不与点 A、E重合),在 AE 同侧分别作正三角形 ABC 和正三角形CDE,AD与BE 交于点O,AD与BC 交于点 P,BE与CD 交于点Q,连接PQ,下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是( )
A.①②③④ B.②③④⑤ C.①③④⑤ D.①②③⑤
10.连接正五边形A 、A 、A 、A 、A ,对角线交出一个正五边形 B B B B B .则以图13-2-7 中线段为边的三角形中,共有等腰三角形( )个.
A.25 B.30 C.35 D.40
11.如图13-2-8所示,在等边三角形ABC中,BD=CE,AD与BE 相交于点 P,则∠APE的度数是( ).
A.45° B.55° C.60° D.75°
12.(1)如图13-2-9所示,A、B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,则符合条件的点C 有( )个.
A.3 B.5 C.8 D.10
(2)等边△ABC,在平面内找一点 P,使△PBC、△PAB、△PAC均为等腰三角形,具备这样条件的 P点有( )个.
A.1 个 B.4 个 C.7 个 D.10 个
13.(1)如图13-2-10所示,四边形ABCD中,AB=BD=DA=AC,则四边形 ABCD中,最大的内角的度数是( ).
A.90° B.120° C.135° D.150°
(2)如图13-2-11 所示,已知O是四边形ABCD 内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( ).
A.70° B.110°
14.(1)等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的底边长为 .
(2)已知等腰三角形的两条边为10、16,那么它的周长等于 .
15.(1)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为 .
(2)已知△ABC的周长为24,AB=AC,AD⊥BC于点D,若△ABD的周长为20,则AD的长为 .
(3)已知等腰三角形的周长为24,腰长为x,则x的取值范围是 .
16.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为 .
17.如图13-2-12 所示,在△ABC 中,AB=AC,AD 是BC 边上的高,点 E、F 是AD 的三等分点,若△ABC的面积为12cm ,则图中阴影部分的面积为 cm .
18.如图13-2-13所示,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF 交AC 于点E,交 BC 于点F.求证:BF=2CF.
19.如图13-2-14所示,在△ABC中,AB=AC,AD=AE.求证:BD=CE.
20.如图13-2-15 所示,已知△ABC 是等腰直角三角形, BE 是 的平分线,DE⊥BC,垂足为 D.
(1)请你写出图中所有的等腰三角形.
(2)请你判断AD 与BE 垂直吗 并说明理由.
(3)如果 BC=10,求AB+AE的长.
21.两个全等的含 角的三角板 ADE 和三角板ABC 按图13-2-16 所示方式放置,E、A、C 三点在一条直线上,连接 BD,取 BD 的中点M,连接 ME、MC.试判断 的形状,并说明理由.
22.如图13-2-17 所示,在△ABC 中, ,BE 平分. 于点D,且AF⊥BC于点 F,交 BE 于点 H.
(1)求证:
(2)探究 BH 与CD 的大小关系,并证明.
23.(1)如图13-2-18所示,在Rt△ABC中,∠ACB=90°,AB 的垂直平分线DE 交于 BC的延长线于点 F,若∠F=30°,DE=1,则 EF 的长是( ).
A.3 B.2 C D.1
(2)如图 13-2-19 所示,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若 EC=1,则EF= .
24.如图13-2-20所示,△ABC是等边三角形,D是AB 边上的一点,以 CD 为边作等边三角形CDE,使点 E、A 在直线DC 的同侧,连接AE.求证:AE∥BC.
巅峰突破
25.如图13-2-21所示,过边长为3的等边三角形ABC的边AB 上一点P,作PE⊥AC 于点E,Q为BC 延长线上一点,当PA=CQ时,连接PQ 交边AC 于点D,则 DE 的长为 .
26.数学课上,李老师出示了如下框中的题目.
在等边三角形 ABC 中,点 E 在AB上,点 D 在CB的延长线上,且ED=EC,如图 13-2-22 所示.试确定线段 AE 与DB 的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况·探索结论
当点 E 为 AB 的中点时,如图 13-2-23(a)所示,确定线段 AE 与 DB 的大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).
(2)特例启发,解答題目
解:题目中,AE与DB 的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图13-2-23(b)所示,过点E作EF∥BC,交 AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点 D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求 CD的长(请你直接写出结果).
27.(1)操作发现:如图 13-2-24(a)所示,D 是等边三角形 ABC 边 BA 上一动点(点 D 与点 B 不重合),连接 DC,以 DC 为边在BC 上方作等边三角形DCF,连接AF.你能发现线段 AF 与BD之间的数量关系吗 并证明你发现的结论.
(2)类比猜想:如图13-2-24(b)所示,当动点 D运动至等边三角形ABC 边BA 的延长线上时,其他作法与(1)相同,猜想AF 与BD 在(1)中的结论是否仍然成立 (直接写出结论)
(3)深入探究
①如图 13-2-24(c)所示,当动点 D 在等边三角形ABC 边BA 上运动时(点 D 与点 B 不重合)连接DC,以 DC 为边在BC 上方、下方分别作等边三角形 DCF 和等边三角形DCF',连接AF、BF',探究 AF、BF'与AB 有何数量关系 并证明你探究的结论.
②如图13-2-24(d)所示,当动点 D 在等边三角形边BA 的延长线上运动时,其他作法与图13-2-24(c)相同,①中的结论是否成立 若不成立,是否有新的结论 并证明你得出的结论.
基础演练
1. D; 2. C; 3.(1)D;(2)D;(3)C
4.4 5.(1)2;(2)等边;9
6.(1)9;(2)3 7.2cm
8.∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
∵∠BAD=40°,∴∠CAD=40°.
∵AD=AE,∴∠ADE=∠AED.
∵∠ADE+∠AED+∠CAD=180°.
∴∠ADE=70°.∵∠ADC=90°,∴∠CDE=20°.
能力提升
9. D;10. C;11. C;12.(1)C;(2)D
13.(1)D;(2)D 14.(1)3cm;(2)42或36
15.(1)4cm或8cm;(2)8;(3)6
18.连接AF,
∵AB=AC,∠BAC=120°,AC的垂直平分线EF 交AC于点E,∴∠B=∠C=30°,AF=CF.
∴∠C=∠FAC=30°,∠BAF=90°.
∴BF=2AF=2CF.
19.过点A作AF⊥BC,垂足为点 F,
∵AB=AC,AF⊥BC,∴BF=CF.
∵AD=AE,AF⊥BC,∴DF=EF.
∴BF-DF=CF-EF.即 BD=CE.
20.(1)△ABD、△AED、△ABC、△DEC.
(2)垂直
证明:∵△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,
∴AE=DE,AB=AC
∵AE=DE,BE=BE.
∴Rt△ABE≌Rt△DBE.
∴AB=BD,∴AD⊥BE.
(3)AB+AE=BD+DE=BD+DC=BC=10.
21.连接MA,
∵∠EAD=30°,∠BAC=60°,∴∠DAB=90°,
∵△EDA≌△CAB,∴DA=AB,ED=AC.
∴△DAB是等腰直角三角形,又 M为BD的中点,
∴∠MDA=∠MBA=45°,AM⊥BD.
∴△DAM与△MAB是等腰直角三角形.
∴AM BD=MD.∴∠EDM=∠MAC=105°
∵ED=AC,∠MDE=∠MAC,MD=AM,
∴△MDE≌△MAC.
∴∠DME=∠AMC,ME=MC,
又∵∠DMA=90°,
∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°.
∴△EMC是等腰直角三角形.
22.(1)延长 BA交CD 延长线于点M.
∵∠MBD=∠CBD,BD⊥CD,BD=BD,
∴△BCD≌△BMD.∴CD=DM CM
∵∠MCA+∠M=90°,∠DBA+∠M=90°,
∴∠MCA=∠DBA.
又∵AC=AB,∠MAC=∠EAB=90°,
∴△MCA≌△EBA.∴CM=BE.
∵CM=2CD,∴BE=2CD.即
(2)连接CH,Rt△CDH中,CH>CD,BH=CH,∴BH>CD.
中考链接
23.(1)B;(2)2
24.∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠ABC=∠BCA=∠ECD=60°,
∴∠BCA-∠DCA=∠ECD-∠DCA.
即∠BCD=∠ACE,∴△ACE≌△BCD.
∴∠EAC=∠DBC=60°=∠ACB.∴AE∥BC.
巅峰突破
25
26.(1)=.(2)=.
证明:在等边△ABC中,
∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,∴∠AEF=∠AFE=60°=∠BAC,
∴AE=AF=EF.
∴AB-AE=AC-AF.即BE=CF.
∵∠ABC=∠EDB+∠BED=60°,∠ACB=∠ECB+∠FCE=60°,
∵ED=EC,∴∠EDB=∠ECB.
∴∠BED=∠FCE.
∵EB=FC,∴△DBE≌△EFC.
∴DB=EF.∴AE=BD.
(3)如下图所示:
27.(1)AF=BD;
证明如下:∵△ABC是等边三角形,
∴BC=AC,∠BCA=60°;
同理可得:DC=CF,∠DCF=60°;
∴∠BCA-∠DCA=∠DCF-∠DCA.
即∠BCD=∠ACF.
∴△BCD≌△ACF.∴BD=AF.
(2)AF=BD.
证明:由(1)知,△BCD≌△ACF.∴BD=AF.
同理△BCF'≌△ACD.
② ①中的结论不成立.新的结论是AF=AB+BF';
∵BC=AC,∠BCF'=∠ACD,F'C=DC,
∴△BCF'≌△ACD.∴BF'=AD.
又由(2)知,AF=BD.
∴AF=BD=AB+AD=AB+BF'.
即AF=AB+BF'.
