第十三章轴对称 综合测试题 (含答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章轴对称 综合测试题 (含答案) 2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 763.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览


文档简介
第十三章轴对称 综合测试题
(满分 100分,时间 90 分钟)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)
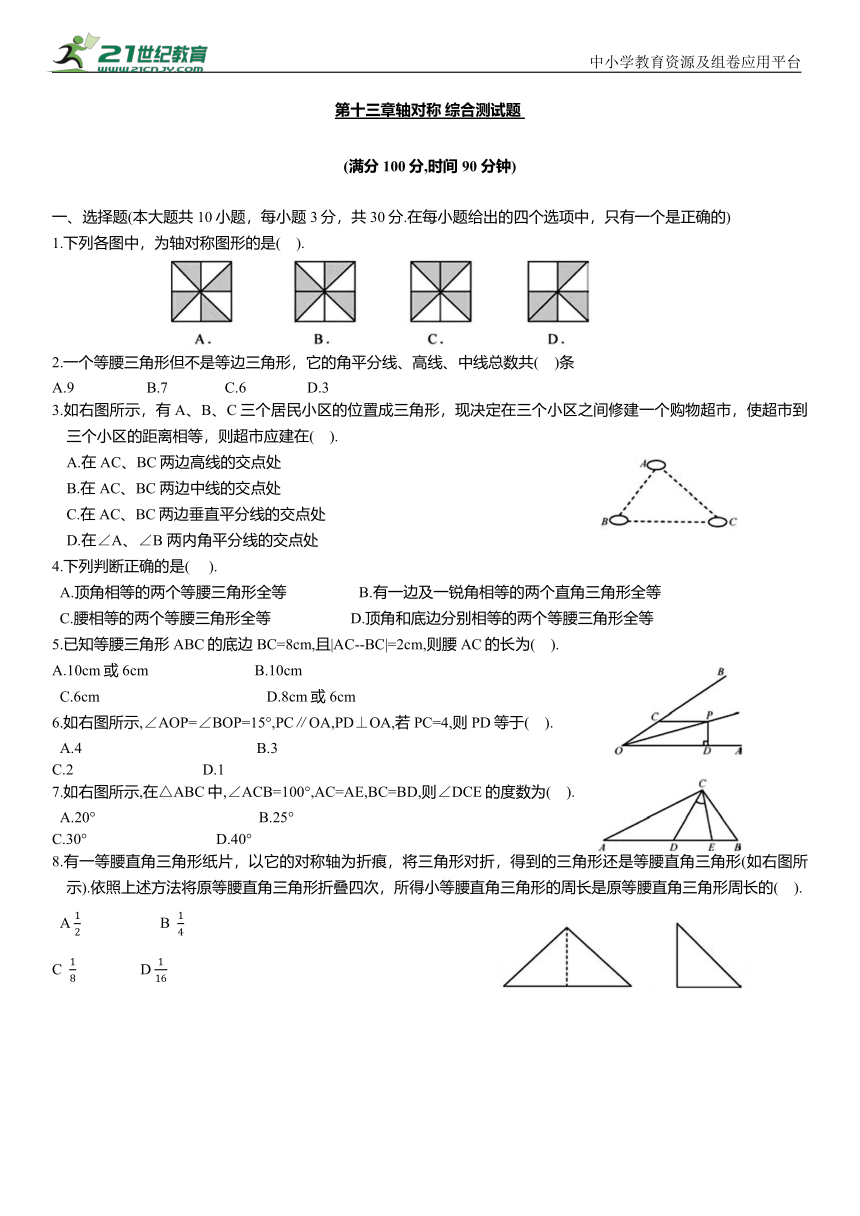
1.下列各图中,为轴对称图形的是( ).
2.一个等腰三角形但不是等边三角形,它的角平分线、高线、中线总数共( )条
A.9 B.7 C.6 D.3
3.如右图所示,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
A.在 AC、BC两边高线的交点处
B.在 AC、BC 两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在∠A、∠B 两内角平分线的交点处
4.下列判断正确的是( ).
A.顶角相等的两个等腰三角形全等 B.有一边及一锐角相等的两个直角三角形全等
C.腰相等的两个等腰三角形全等 D.顶角和底边分别相等的两个等腰三角形全等
5.已知等腰三角形ABC的底边BC=8cm,且|AC--BC|=2cm,则腰AC的长为( ).
A.10cm或6cm B.10cm
C.6cm D.8cm或 6cm
6.如右图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则 PD等于( ).
A.4 B.3
C.2 D.1
7.如右图所示,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为( ).
A.20° B.25°
C.30° D.40°
8.有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如右图所示).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的( ).
A B
中小学教育资源及组卷应用平台
C D
9.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如右图所示),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( ).
A.1 个 B.2个
C.3个 D.4个
10.在平面直角坐标系中,已知A(-3,3),在y轴上确定一点 P,使△AOP 为等腰三角形,则符合条件的点 P 共有( ).
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共10小题,每小题2分,共20分)
11. 如右图所示,在△ABC 中,∠B= 80°,DE 是 AC 的垂直平分线,且∠BAD:∠BAC=1:3,则∠C= 度.
12.等腰三角形ABC中,AB=AC=10,∠A=30°,则腰AB上的高等于 .
13.有一个内角为 60°的等腰三角形,腰长为 6cm,那么这个三角形的周长为 cm.
14.等腰三角形两腰上的高相交所成的钝角为 100°,则顶角的度数为 ,底角的度数为 .
15.如下左图所示,已知在等腰三角形ABC中,AB=AC,AE∥BC.∠BAC=40°,∠DAE= °.
16.如下中图所示,BD垂直平分线段AC,AE⊥BC,垂足为 E,交 BD 于 P 点,PE=3cm,则 P 点到直线AB 的距离是 cm.
17.如下右图所示,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有 个.
18.如右图所示,在Rt△ABC中,CD 是斜边AB 上的高,角平分线 AE 交CD于点H,EF⊥AB于点F,有下列结论:①∠ACD=∠B;②CH=CE=EF;③AC = AF;④CH = HD;⑤ BE = CH. 其 中 你 认 为 正 确 的 有 .(填序号就可以)
19.将一张纸片沿任一方向翻折,得到折痕 AB(如图(a)所示);再翻折一次,得到折痕OC(如图(b)所示);翻折使OA与OC 重合,得到折痕OD(如图(c)所示);最后翻折使OB 与OC 重合,得到折痕 OE(如图(d)所示).展开恢复成图(e)形状,则∠DOE 的大小是 .
20.图(a)是一块边长为1,周长记为 的正三角形纸板,沿图(a)的底边剪去一块边长为 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图(c),(d),…,记第n 块纸板的周长为 则 ;P -P =_.
三、解答题(21~26题每题6分,27,28题每题7分)
21.如右图所示,在 中, ,ED 是AC 的垂直平分线,交 AC 于点 D,交 BC于点 E.已知 求 的度数.
22.如右图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
23.如右图所示,在△ABC中,已知AB=AC,AD为∠BAC的平分线,且 求 C 和∠B 的度数.
24.如右图所示,在△ABC中,AH⊥BC于点H,∠C=35°,且, ,求∠B 度数.
25.如右图所示,已知 和直线MN.求作: 使 和 关于直线MN 对称.(不要求写作法,只保留作图痕迹)
26.如右图所示,已知等边三角形ABC外有一点P,P落在 内,设点 P到BC、CA、AB三边的距离分别为 h 、h 、h ,且满足 求△ABC的面积.
27.如右图所示,在△ABC中,AB=BC=AC,AE=CD,AD 与BE 相交于点 P,BQ⊥AD于点Q.
求证:(1)△ADC≌△BEA;(2)BP=2PQ.
28.如右图所示,在 中,AD 交 BC 于点 D,点 E 是 BC 中点, 交CA 的延长线于点 F,交AB 于点G,若 AD 为 的角平分线,求证:
一、选择题
1. C; 2. B; 3. C; 4. D; 5. A; 6. C;
7. D; 8. B; 9. C; 10. C
二、填空题
11.40; 12.5; 13.18;
14.100°或 80°;40°或50°; 15.70; 16.3;
17.3; 18.①②③; 19.90°;
三、解答题
21.∠C=40°. 22.77°,38.5°. 23.50°和65°
24.在 CH 上截取 DH=BH,连结 AD,先证△ABH≌△ADH,再证∠C=∠DAC,得到∠B=70°.
25.图略
26.设等边△ABC的边长为a,
连接 PA、PB、PC,
则
即
27.(1)∵AB=BC=AC,
∴△ABC是等边三角形.∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,∴△ADC≌△BEA.
(2)∵△ADC≌△BEA,∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.∴∠BPQ=60°.
∵BQ⊥AD,∴∠PBQ=30°.∴BP=2PQ.
28.延长FE到点 H,使 HE=FE,连接BH.
∵CE=BE,∠CEF=∠BEH,FE=HE.
∴△CEF≌△BEH.∴∠F=∠H,CF=BH.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵AD∥EF,
∴∠BAD=∠AGF=∠CAD=∠F=∠BGH.
∴∠BHG=∠BGH.∴BG=BH.∴BG=CF.
(满分 100分,时间 90 分钟)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)
1.下列各图中,为轴对称图形的是( ).
2.一个等腰三角形但不是等边三角形,它的角平分线、高线、中线总数共( )条
A.9 B.7 C.6 D.3
3.如右图所示,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
A.在 AC、BC两边高线的交点处
B.在 AC、BC 两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在∠A、∠B 两内角平分线的交点处
4.下列判断正确的是( ).
A.顶角相等的两个等腰三角形全等 B.有一边及一锐角相等的两个直角三角形全等
C.腰相等的两个等腰三角形全等 D.顶角和底边分别相等的两个等腰三角形全等
5.已知等腰三角形ABC的底边BC=8cm,且|AC--BC|=2cm,则腰AC的长为( ).
A.10cm或6cm B.10cm
C.6cm D.8cm或 6cm
6.如右图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则 PD等于( ).
A.4 B.3
C.2 D.1
7.如右图所示,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为( ).
A.20° B.25°
C.30° D.40°
8.有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如右图所示).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的( ).
A B
中小学教育资源及组卷应用平台
C D
9.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如右图所示),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( ).
A.1 个 B.2个
C.3个 D.4个
10.在平面直角坐标系中,已知A(-3,3),在y轴上确定一点 P,使△AOP 为等腰三角形,则符合条件的点 P 共有( ).
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共10小题,每小题2分,共20分)
11. 如右图所示,在△ABC 中,∠B= 80°,DE 是 AC 的垂直平分线,且∠BAD:∠BAC=1:3,则∠C= 度.
12.等腰三角形ABC中,AB=AC=10,∠A=30°,则腰AB上的高等于 .
13.有一个内角为 60°的等腰三角形,腰长为 6cm,那么这个三角形的周长为 cm.
14.等腰三角形两腰上的高相交所成的钝角为 100°,则顶角的度数为 ,底角的度数为 .
15.如下左图所示,已知在等腰三角形ABC中,AB=AC,AE∥BC.∠BAC=40°,∠DAE= °.
16.如下中图所示,BD垂直平分线段AC,AE⊥BC,垂足为 E,交 BD 于 P 点,PE=3cm,则 P 点到直线AB 的距离是 cm.
17.如下右图所示,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有 个.
18.如右图所示,在Rt△ABC中,CD 是斜边AB 上的高,角平分线 AE 交CD于点H,EF⊥AB于点F,有下列结论:①∠ACD=∠B;②CH=CE=EF;③AC = AF;④CH = HD;⑤ BE = CH. 其 中 你 认 为 正 确 的 有 .(填序号就可以)
19.将一张纸片沿任一方向翻折,得到折痕 AB(如图(a)所示);再翻折一次,得到折痕OC(如图(b)所示);翻折使OA与OC 重合,得到折痕OD(如图(c)所示);最后翻折使OB 与OC 重合,得到折痕 OE(如图(d)所示).展开恢复成图(e)形状,则∠DOE 的大小是 .
20.图(a)是一块边长为1,周长记为 的正三角形纸板,沿图(a)的底边剪去一块边长为 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图(c),(d),…,记第n 块纸板的周长为 则 ;P -P =_.
三、解答题(21~26题每题6分,27,28题每题7分)
21.如右图所示,在 中, ,ED 是AC 的垂直平分线,交 AC 于点 D,交 BC于点 E.已知 求 的度数.
22.如右图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
23.如右图所示,在△ABC中,已知AB=AC,AD为∠BAC的平分线,且 求 C 和∠B 的度数.
24.如右图所示,在△ABC中,AH⊥BC于点H,∠C=35°,且, ,求∠B 度数.
25.如右图所示,已知 和直线MN.求作: 使 和 关于直线MN 对称.(不要求写作法,只保留作图痕迹)
26.如右图所示,已知等边三角形ABC外有一点P,P落在 内,设点 P到BC、CA、AB三边的距离分别为 h 、h 、h ,且满足 求△ABC的面积.
27.如右图所示,在△ABC中,AB=BC=AC,AE=CD,AD 与BE 相交于点 P,BQ⊥AD于点Q.
求证:(1)△ADC≌△BEA;(2)BP=2PQ.
28.如右图所示,在 中,AD 交 BC 于点 D,点 E 是 BC 中点, 交CA 的延长线于点 F,交AB 于点G,若 AD 为 的角平分线,求证:
一、选择题
1. C; 2. B; 3. C; 4. D; 5. A; 6. C;
7. D; 8. B; 9. C; 10. C
二、填空题
11.40; 12.5; 13.18;
14.100°或 80°;40°或50°; 15.70; 16.3;
17.3; 18.①②③; 19.90°;
三、解答题
21.∠C=40°. 22.77°,38.5°. 23.50°和65°
24.在 CH 上截取 DH=BH,连结 AD,先证△ABH≌△ADH,再证∠C=∠DAC,得到∠B=70°.
25.图略
26.设等边△ABC的边长为a,
连接 PA、PB、PC,
则
即
27.(1)∵AB=BC=AC,
∴△ABC是等边三角形.∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,∴△ADC≌△BEA.
(2)∵△ADC≌△BEA,∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.∴∠BPQ=60°.
∵BQ⊥AD,∴∠PBQ=30°.∴BP=2PQ.
28.延长FE到点 H,使 HE=FE,连接BH.
∵CE=BE,∠CEF=∠BEH,FE=HE.
∴△CEF≌△BEH.∴∠F=∠H,CF=BH.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵AD∥EF,
∴∠BAD=∠AGF=∠CAD=∠F=∠BGH.
∴∠BHG=∠BGH.∴BG=BH.∴BG=CF.
