沪科版七年级上册 2.2代数式 课件

课件36张PPT。代数式一、基本概念：用运算符号(＋、×、÷、乘方、开方)把数或表示数的字母连结而成的式子．单独 的一个数字和字母也叫代数式.2．系数： 在代数式中，字母前面的数字因数 (连同符号)称为它的系数．1．代数式：3．同类项：所含字母相同，并且相同字母的指数也分别相同的项．用数字代替代数式里的字母,按运算顺序计算后所得到的结果.4．代数式的值:５．合并同类项：把几个同类项合并成一项．把同类项的系数相加，字母和字母的指数不变．６．去括号法则：括号前面是“＋”号，把括号和它前面是“＋”号去掉，括号里的各项都不变．
括号前面是“－”号，把括号和它前面是“－”号去掉，括号里的各项都要改变．列代数式要注意以下几点:数字与字母、字母与字母相乘，要把乘号省略；如：2×a写作2a、a×b写作ab、 2×(a+b)或（ a+b）×２写作　2(a+b)．1．(1)用代数式表示“比a的平方的2倍小1的数”
为( )
A．2a2－1 B．(2a)2－1
C．2(a－1)2 D．(2a－1)2A二、列代数式降了４０％ a, 则降价
后此药的价格是：
a －40% a = (1- 40%)(2)．将原价为a的某种常用药降价40%，
　　则降价后此药的价格是＿＿＿＿元． (1- 40%)a(3)某种品牌的彩电降价30%后，
每台售价为a元，则该品牌彩电
每台原价为________ 元 (4).如图，正方形的边长为a，以各边为
直径在正方形内画半圆，所围成图
形的面积为____________． (5)有一大捆同种型号的电线，现要确定其长度，
从中先取一段电线，称出它的质量为a千克，
量出它的长度为m米，再称得其余电线的总
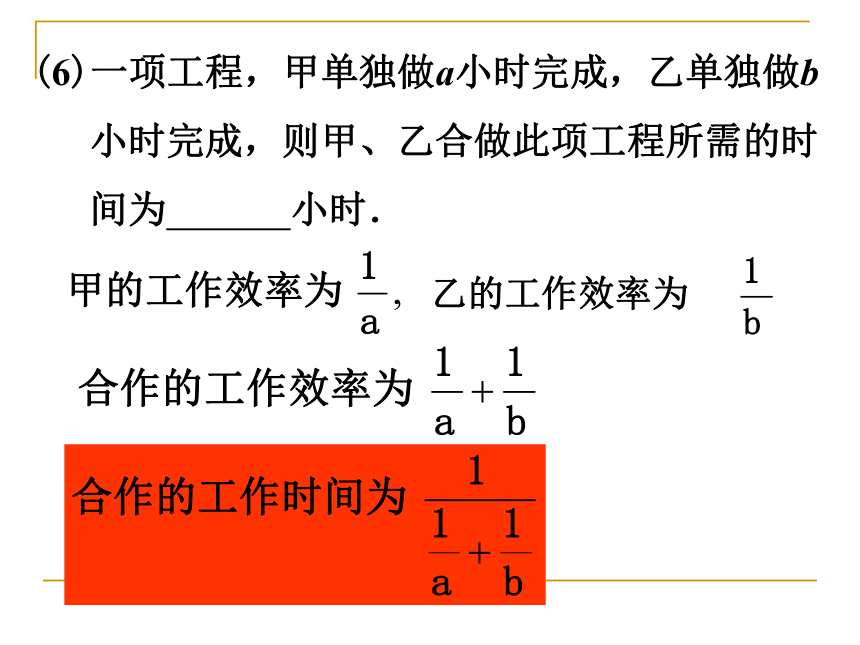
质量为b千克，则这捆电线的总长度为 米． 则这捆电线的总长度为:(6)一项工程，甲单独做a小时完成，乙单独做b
小时完成，则甲、乙合做此项工程所需的时
间为 小时． (7)第12届电视剧飞天奖今年有a部作品参
赛，比去年增加了40%，还多2部，
则去年参赛的作品有 部． 设:去年参赛的作品有x部．则:

(1+40%)x+2=a , (1+40%)x=a-2三、基本概念运用:3ba(2)下列各组中，同类项是( )
A．3x2y与－3xy2 B．3xy与－2yx
C．2x与2x2 D．5xy与5yzB324.下列式子正确的是( ).D5. 化简（5a－3b) －3（a2－2b )解： （5a－3b) －3（a2－2b )
＝ 5a－3b －（3 a2 －6b )
熟练后此式可省略
＝ 5a－3b － 3 a2 ＋6b
括号前是负要变号
＝5a＋3b － 3 a2
同类项记得要合并
注意!
正确使用
乘法分配律7.按程序:( ) ×3－ (－2) 输入一个数所得
到的代数式的值是14,则输入这个数是____.由( ) ×3 + 2 = 14 得:
14－2 = ( ) ×3
12 = ( ) ×3 ,
( ) = 44(3)定义运算：a※b＝ab＋a＋b－1，
验证下列运算成立的是( )
A．a※b＝(－a)※(－b)
B．a※(－b)＝(－a)※b
C．a※b＝b※a
D．a※(b※c)＝(a※b)※c C(-a).(-b)-a-b-1a.(-b)+a-b-1-a.b-a+b-1ba+b+a-11.某商场文具部的某种毛笔每支售价25元，书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式：第一种：买一支毛笔附赠一本书法练习本；第二种：按购买金额打九折付款。八年级（5）班的小明想为本班书法兴趣小组购买这种毛笔10支，书法练习本 x（x≥10）本。
(1).用代数式分别表示两种购买方式应支付的金额.
(2).若小明想为本班书法兴趣小组购买书法练习本30 本,试问小明应该选择哪一种优惠方式才更省钱？ 四.代数式应用:某商场文具部的某种毛笔每支售价25元，书 法练习本每本售价5元。该商场为促销制定了如下两种优惠方式：第一种：买一支毛笔附赠一本书法练习本；第二种：按购买金额打九折付款。八年级（5）班的小明想为本班书法兴趣小组购买这种毛笔10支，书法练习本 x（x≥10）本。
(1).用代数式分别表示两种购买方式应支付的金额.解:设买练习本x,则得两种购买方法的代数式为:(1).代数式分别为:25×10+5(x-10),(25×10+5x) ×90%1.某商场文具部的某种毛笔每支售价25元，书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式：第一种：买一支毛笔附赠一本书法练习本；第二种：按购买金额打九折付款。八年级（5）班的小明想为本班书法兴趣小组购买这种毛笔10支，书法练习本 x（x≥10）本。
(2).若小明想为本班书法兴趣小组购买书法练习本30 本,试问小明应该选择哪一种优惠方式才更省钱？ (2).25×10+5(x-10) =25×10+5(30-10) =350(25×10+5x) ×90%解:把X=30分别代入两个代数式:(25×10+5×30) ×90% =360所以选择第一种优惠方式五.探索规律:1.如图，是由边长为1的正方形按照某种 规律排列而成的：①②③(1)观察图形，填写下表：
(2)推测第n个图形中，正方形的个数为
__________，周长为_____________．
(用含n的代数式表示)13185n+3283810n+82.数学兴趣小组的同学用棋子摆了如下三
个“工”字形图案：
按照这种规律，摆第4个“工”字形图案需要____
个棋子；摆第n个图案需要__________个棋子．○ ○ ○○○ ○ ○○ ○ ○ ○ ○○○ ○ ○ ○ ○○○ ○ ○ ○ ○ ○ ○○○○ ○ ○ ○ ○ ○ ○○225n+23.如图，在2005年3月的日历上：(1)任意圈出一竖
列上相邻的三个
数，设中间的一个
数为x，则其余两
个数分别为 ． 3x4.如图，在2005年3月的日历上：(2)用一个矩形框
出四个数 ，
请用一个等式表示
a、b、c、d之间的
关系: a b c da=b-1=c-7=d-85.如图，在2005年3月的日历上：(3)用一个十字框
任意框出5个数，
设中间一个数为
a，则框出的5个数
的和为 ． 5a再见二、例题：【例6】设a＝(x1，y1)，b＝(x2，y2)，定义运算：
， ．
(1)若a＝(1，－2)，b＝(－1，2)，求 及
的值．
(2)若a＝(x，－2)，b＝(1，x)，是否存在x，使
＝ ？若存在，求出x的值；否则，
请说明理由．二、例题：【例2】
(6)随着计算机技术的迅猛发展，电脑的价格不
断降低，某种品牌电脑按原售价降低m元后，
又降低20%，现售价为n元，则该电脑的原售
价为 元． 二、例题：【例7】某企业有九个生产车间，现在每个车间原有的成
品一样多，每个车间每天生产的成品也一样多．有A、B
两组检验员，其中A组有8名检验员，他们先用两天将第
一、二车间的所有成品 (指原有的和后来生产的)检验完
毕后，再去检验第三、四两个车间的所有成品，又用了
三天时间，同时，用这五天时间，B组检验员也检验完
余下的五个车间的所有成品．若每个检验员的检验速度
相同，每个车间原有的成品为a件，每个车间每天生产b
件成品．(1)试用a、b表示B组检验员检验的成品总数；二、例题：【例7】某企业有九个生产车间，现在每个车间原有的成
品一样多，每个车间每天生产的成品也一样多．有A、B
两组检验员，其中A组有8名检验员，他们先用两天将第
一、二车间的所有成品 (指原有的和后来生产的)检验完
毕后，再去检验第三、四两个车间的所有成品，又用了
三天时间，同时，用这五天时间，B组检验员也检验完
余下的五个车间的所有成品．若每个检验员的检验速度
相同，每个车间原有的成品为a件，每个车间每天生产b
件成品．(2)求B组检验员的人数．三、作业：
1．《中考指导》P19—20 1、4、5
2．某商店积压了100件某种商品，为使这批货物
尽快脱手，该商店采取了如小销售方案：将价格
提高到原来的2.5倍，再作三次降价处理：第一次
降价30%，标出“亏本价”；第二次降价30%，
标出“破产价”；第三次降价30%，标出“跳楼
价”．三次降价处理销售结果如下表：三、作业：
(1)求跳楼价占原价的百分比；
(2)该商品按新方案销售，相比按原价销售，哪
种方式更盈利？