北师大版三年级下册 对列表演(一)教学设计
文档属性
| 名称 | 北师大版三年级下册 对列表演(一)教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 355.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览

文档简介
北师大版小学数学三年级下册
队列表演(一)教学设计
教学目标:
1.结合“队列表演”的具体情境,利用点子图探索两位数乘两位数的计算方法,理解算理。
2. 经历交流各自算法的过程,体验算法的多样化。
3.正确进行两位数乘两位数的乘法的横式笔算,并选择合理简洁的运算途径。
教学流程:
【课前】
写好标题,贴好点子图。
【视频导入】
播放阅兵视频。
同学们,刚才我们看到的是我们国庆节70周年的大阅兵视频,你觉得阅兵仪式怎么样?(生答:非常震撼)
是的,国庆节有阅兵仪式,淘气学校里也有类似的队列表演,看这组队列一共有12行,每行14人。整齐的队列,如果把每个人看成一个点,就像我们数学上的?(生:点子图)课件出示点子图
【问题探究】
“这里有多少人参加队列表演?”“你想用什么办法算出来”抽学生回答
导向:先求出小部分,再把小部分加起来。
(一)生独立探究
请同学们在学习单第一题里圈出你的小部分点子,再把小部分都加起来算一算。
完成一种方法的,小组之间交流分享一下,再新增一种圈法。
教师收集4种不同的,较为典型的圈法,出示在投影上
①你能看懂几种?——用手指告诉我。
②让他本人介绍一下(跟他一样的可以拍手表示一下)
师生一起探究
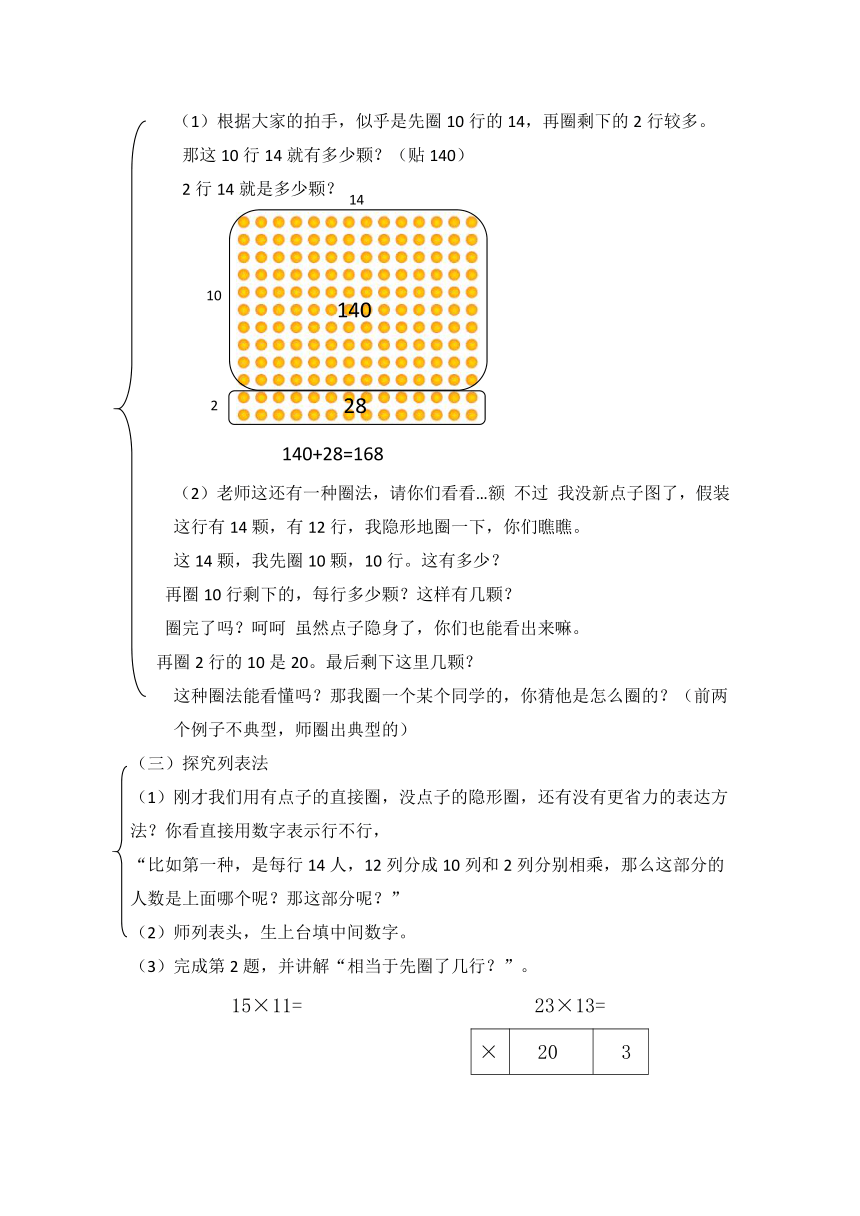
(1)根据大家的拍手,似乎是先圈10行的14,再圈剩下的2行较多。
那这10行14就有多少颗?(贴140)
2行14就是多少颗?
140+28=168
(2)老师这还有一种圈法,请你们看看…额 不过 我没新点子图了,假装这行有14颗,有12行,我隐形地圈一下,你们瞧瞧。
这14颗,我先圈10颗,10行。这有多少?
再圈10行剩下的,每行多少颗?这样有几颗?
圈完了吗?呵呵 虽然点子隐身了,你们也能看出来嘛。
再圈2行的10是20。最后剩下这里几颗?
这种圈法能看懂吗?那我圈一个某个同学的,你猜他是怎么圈的?(前两个例子不典型,师圈出典型的)
(三)探究列表法
(1)刚才我们用有点子的直接圈,没点子的隐形圈,还有没有更省力的表达方法?你看直接用数字表示行不行,
“比如第一种,是每行14人,12列分成10列和2列分别相乘,那么这部分的人数是上面哪个呢?那这部分呢?”
师列表头,生上台填中间数字。
完成第2题,并讲解“相当于先圈了几行?”。
15×11= 23×13=
× 20 3
10
3
× 15
10
1
【练习巩固】
3.用自己喜欢的方式计算下面算式。
11×11= 12×11= 13×13= 31×13=
一共需要多少元?
照例子,算一算。
13×11=13×10 + 13×1=130 + 13=143
14×21=14× +14× = + =
15×31=
16×41=
你最喜欢哪种乘法的计算方法?在最喜欢的方法下面画一个 。
圈点子图法(如题1) 列表法(如题2) 横式法(如题5) 其他:
【课堂小结】
学了这节课,你有什么收获?
【板书】
队列表演(一)
有多少人参加队列表演?圈一圈,算一算。
14×12=
× 14
10
2
× 10 4
10
2
10
2
14
140
28
+
+
+
+
=
=
140+28=168
2×14=28
14×10=140
10
10×10=100
4
2
4
2
10
100+40+20+8=168
2×10=20
2×4=8
4×10=40
队列表演(一)教学设计
教学目标:
1.结合“队列表演”的具体情境,利用点子图探索两位数乘两位数的计算方法,理解算理。
2. 经历交流各自算法的过程,体验算法的多样化。
3.正确进行两位数乘两位数的乘法的横式笔算,并选择合理简洁的运算途径。
教学流程:
【课前】
写好标题,贴好点子图。
【视频导入】
播放阅兵视频。
同学们,刚才我们看到的是我们国庆节70周年的大阅兵视频,你觉得阅兵仪式怎么样?(生答:非常震撼)
是的,国庆节有阅兵仪式,淘气学校里也有类似的队列表演,看这组队列一共有12行,每行14人。整齐的队列,如果把每个人看成一个点,就像我们数学上的?(生:点子图)课件出示点子图
【问题探究】
“这里有多少人参加队列表演?”“你想用什么办法算出来”抽学生回答
导向:先求出小部分,再把小部分加起来。
(一)生独立探究
请同学们在学习单第一题里圈出你的小部分点子,再把小部分都加起来算一算。
完成一种方法的,小组之间交流分享一下,再新增一种圈法。
教师收集4种不同的,较为典型的圈法,出示在投影上
①你能看懂几种?——用手指告诉我。
②让他本人介绍一下(跟他一样的可以拍手表示一下)
师生一起探究
(1)根据大家的拍手,似乎是先圈10行的14,再圈剩下的2行较多。
那这10行14就有多少颗?(贴140)
2行14就是多少颗?
140+28=168
(2)老师这还有一种圈法,请你们看看…额 不过 我没新点子图了,假装这行有14颗,有12行,我隐形地圈一下,你们瞧瞧。
这14颗,我先圈10颗,10行。这有多少?
再圈10行剩下的,每行多少颗?这样有几颗?
圈完了吗?呵呵 虽然点子隐身了,你们也能看出来嘛。
再圈2行的10是20。最后剩下这里几颗?
这种圈法能看懂吗?那我圈一个某个同学的,你猜他是怎么圈的?(前两个例子不典型,师圈出典型的)
(三)探究列表法
(1)刚才我们用有点子的直接圈,没点子的隐形圈,还有没有更省力的表达方法?你看直接用数字表示行不行,
“比如第一种,是每行14人,12列分成10列和2列分别相乘,那么这部分的人数是上面哪个呢?那这部分呢?”
师列表头,生上台填中间数字。
完成第2题,并讲解“相当于先圈了几行?”。
15×11= 23×13=
× 20 3
10
3
× 15
10
1
【练习巩固】
3.用自己喜欢的方式计算下面算式。
11×11= 12×11= 13×13= 31×13=
一共需要多少元?
照例子,算一算。
13×11=13×10 + 13×1=130 + 13=143
14×21=14× +14× = + =
15×31=
16×41=
你最喜欢哪种乘法的计算方法?在最喜欢的方法下面画一个 。
圈点子图法(如题1) 列表法(如题2) 横式法(如题5) 其他:
【课堂小结】
学了这节课,你有什么收获?
【板书】
队列表演(一)
有多少人参加队列表演?圈一圈,算一算。
14×12=
× 14
10
2
× 10 4
10
2
10
2
14
140
28
+
+
+
+
=
=
140+28=168
2×14=28
14×10=140
10
10×10=100
4
2
4
2
10
100+40+20+8=168
2×10=20
2×4=8
4×10=40
