22.3 第3课时 建立适当坐标系解决实际问题 课件(共20张PPT)【人教九上数学精简课堂课件】
文档属性
| 名称 | 22.3 第3课时 建立适当坐标系解决实际问题 课件(共20张PPT)【人教九上数学精简课堂课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 06:58:58 | ||
图片预览







文档简介
(共20张PPT)
人教九上数学同步精品课件
人教版九年级上册
人教版九(上)数学精简课堂课件
第二十二章 二次函数
第3课时 建立适当坐标系
解决实际问题
随堂演练
获取新知
情景导入
例题讲解
知识回顾
课堂小结
22.3 实际问题与二次函数>
情景导入
抛物线形结构在生活中到处可见.
获取新知
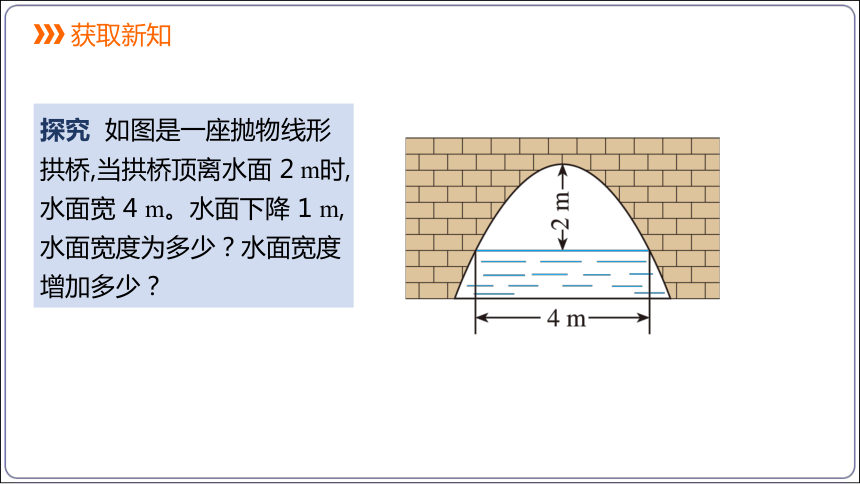
探究 如图是一座抛物线形拱桥,当拱桥顶离水面 2 m时,水面宽 4 m。水面下降 1 m, 水面宽度为多少?水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
当水面下降1 m时,水面的纵坐标为-3.
当y=-3时,- x2=-3,解得x1= ,x2=- (舍去).
所以当水面下降1 m时,水面宽度为 m.
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=- x2.
水面下降1 m,水面宽度增加 m.
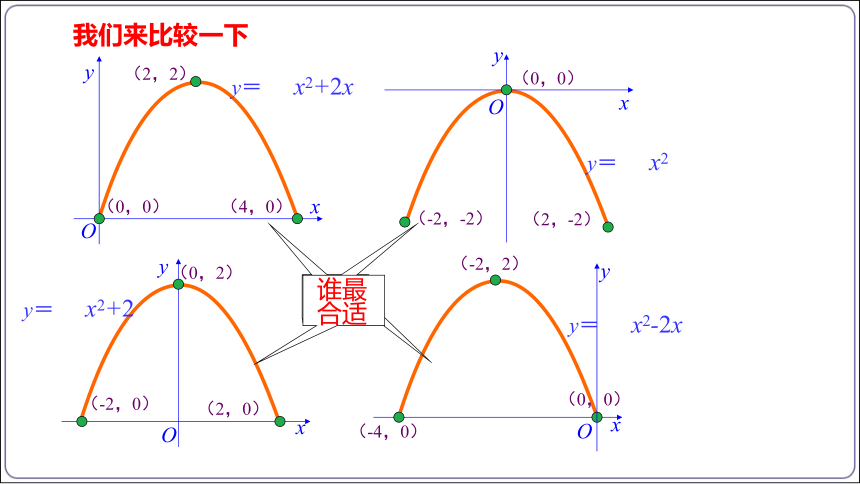
思考:这样建立坐标系后,这条抛物线表示的二次函数是y=ax2的形式,能否建立其它的坐标系解决问题吗?请您试着做一做,并比较怎么样的坐标系可使抛物线表示的二次函数形式更简单?
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最
合适
y
y
O
O
x
x
x
x
y
y
O
O
y= x2+2
y= x2
y= x2+2x
y= x2-2x
建立坐标系解决实际问题“三步骤”:
1.建:根据题意,建立恰当的坐标系,设抛物线解析式;
2.转:准确转化线段的长与点的坐标之间的关系,得到
抛物线上点的坐标,
3.求:代入解析式,求出二次函数解析式;
4.用:应用所求解析式及性质解决问题.
知识要点
例1 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
例题讲解
解:如图,建立直角坐标系,则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
A
B
C
解得
a=-0.2,
k=3.5,
设抛物线的表达式为 y=ax2+k ,所以有
2.25a+k=3.05,
k=3.5,
所以该抛物线的表达式为y=-0.2x2+3.5.
当 x=-2.5时,y=2.25 .
故该运动员出手时的高度为2.25m.
例2 某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其他因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
● B(1,2.25)
(0,1.25)
●
C
●
D
o
A
x
y
解:建立如图所示的坐标系.
根据对称性,如果不计其他因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;
同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
● B(1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
随堂演练
1. 河北省赵县的赵州桥的桥拱近似的抛物线型,建立如图所示的平面直角坐标系,其函数的关系式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB 为( )
A.-20 m B.10 m
C.20 m D.-10 m
C
2.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 米.
x
y
O
2
3.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
课堂小结
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标
选择运算简便的坐标系
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
人教版九(上)数学精简课堂课件
第二十二章 二次函数
第3课时 建立适当坐标系
解决实际问题
随堂演练
获取新知
情景导入
例题讲解
知识回顾
课堂小结
22.3 实际问题与二次函数>
情景导入
抛物线形结构在生活中到处可见.
获取新知
探究 如图是一座抛物线形拱桥,当拱桥顶离水面 2 m时,水面宽 4 m。水面下降 1 m, 水面宽度为多少?水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
当水面下降1 m时,水面的纵坐标为-3.
当y=-3时,- x2=-3,解得x1= ,x2=- (舍去).
所以当水面下降1 m时,水面宽度为 m.
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=- x2.
水面下降1 m,水面宽度增加 m.
思考:这样建立坐标系后,这条抛物线表示的二次函数是y=ax2的形式,能否建立其它的坐标系解决问题吗?请您试着做一做,并比较怎么样的坐标系可使抛物线表示的二次函数形式更简单?
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最
合适
y
y
O
O
x
x
x
x
y
y
O
O
y= x2+2
y= x2
y= x2+2x
y= x2-2x
建立坐标系解决实际问题“三步骤”:
1.建:根据题意,建立恰当的坐标系,设抛物线解析式;
2.转:准确转化线段的长与点的坐标之间的关系,得到
抛物线上点的坐标,
3.求:代入解析式,求出二次函数解析式;
4.用:应用所求解析式及性质解决问题.
知识要点
例1 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
例题讲解
解:如图,建立直角坐标系,则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
A
B
C
解得
a=-0.2,
k=3.5,
设抛物线的表达式为 y=ax2+k ,所以有
2.25a+k=3.05,
k=3.5,
所以该抛物线的表达式为y=-0.2x2+3.5.
当 x=-2.5时,y=2.25 .
故该运动员出手时的高度为2.25m.
例2 某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其他因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
● B(1,2.25)
(0,1.25)
●
C
●
D
o
A
x
y
解:建立如图所示的坐标系.
根据对称性,如果不计其他因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;
同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
● B(1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
随堂演练
1. 河北省赵县的赵州桥的桥拱近似的抛物线型,建立如图所示的平面直角坐标系,其函数的关系式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB 为( )
A.-20 m B.10 m
C.20 m D.-10 m
C
2.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 米.
x
y
O
2
3.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
课堂小结
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标
选择运算简便的坐标系
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
