(分班考试)2024年小升初数学(新初一)名校分班考试模拟检测卷(二)人教版(含解析)
文档属性
| 名称 | (分班考试)2024年小升初数学(新初一)名校分班考试模拟检测卷(二)人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 436.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览




文档简介
(分班考试)2024年小升初数学(新初一)名校分班考试检测卷(二)
学校:___________姓名:___________班级:___________考号:___________
一、选择题(每题2分,共12分)
1.有关部门要连续审核30个科研课题方案,如果要求每天安排审核的课题个数互不相等且不为零,则审核完这些课题最多需要( )。
A.7天 B.8天 C.9天 D.10天
2.红红按照一定的规律用小棒摆出了下面的4幅图。
如果按照这个规律继续摆,第五幅图要用( )根小棒。
A.23 B.31 C.35 D.45
3.将分别写有2,3,7,8四个数字的二张卡片反扣在桌面上,任意抽两张,和是奇数的可能性 和是偶数的可能性。
A.大于 B.小于 C.等于 D.无法确定
4.有两根铁丝,第一根用去米,第二根用去,剩下的一样长,两根铁丝原来相比( )。
A.第一根长 B.一样长 C.无法确定
5.某S为自然数,被10除余数是9,被9除余数是8,被8除余数是7,已知100<S<1000,请问这样的数有几个?( )
A.5 B.4 C.3 D.2
6.爸爸有2万元钱,有两种理财方式:一种是买3年期国债,年利率为4%;另一种是买银行1年期理财产品,年收益率是4%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大( )。
A.国债 B.理财产品 C.一样大 D.无法确定
二、填空题(每空1.5分,共21分)
7.用f(n)表示组成n的数字中不是零的几个数字乘积,例如:f(5)=5;f(29)=18; f(207)=14.则f(1)+f(2)+f(3)+…+f(99)+f(100)=( ).
8.A、B、C、D四个同学在一次数学考试中的成绩分别为97分、92分、88分和90分.这四个同学的平均分是( )分;若每个同学增加1分,平均分是( )分;若每个同学增加X分,那么这四人的平均分是( )分;若四个同学的成绩增加相同的分数,平均成绩最多是( )分(满分为100分)
9.尼尔斯在骑鹅旅行时来到一个小岛上,这里不论是谁,每星期都有几天说真话,有几天则说假话.有一天,尼尔斯遇到狐狸和狼,狐狸说:“每星期一、二、三是我说谎的日子.”而狼说:“每星期四、五、六是我说谎的日子,刚才狐狸说的不是真话!”三天后,尼尔斯又遇到它们,他已经知道这天狐狸说的是真话,这天狼说的是( )话.
10.聪聪在探究圆柱体积时,先把圆柱体拼成一个近似长方体,再把这个长方体侧放,他发现了一种更巧妙的方法(如图)。如果圆柱的底面半径是4厘米,侧面积是251.2平方厘米,这个圆柱的体积是( )立方厘米。
11.一盘草莓约20个左右,几位小朋友分.若每人分3个,则余下2个;若每人分4个,则差3个.这盘草莓有( )个.
12.某厂甲车间有工人180人,乙车间有工人120人,现从两车间共调出50名工人支援新厂,余下工人因工作量增加,每人每天增加工资20%,因工种不同,甲车间工人每人每天工资60元,乙车间工人每人每天工资48元,已知工厂每天所发工资总额与以前相同,甲车间现有工人( )人。
13.一桶农药,第一次倒出2/7然后倒回桶内120克,第二次倒出桶中剩下农药的3/8,第三次倒出320克,桶中还剩下80克,原来桶中有农药( )克.
14.甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲志愿者计划完成此项工作的天数是( )天。
15.如图,三角形EFC的面积是24平方厘米,AE=CE,BF=FC,则三角形ABC的面积为( )平方厘米。
16.把4个直径是4厘米的圆柱形饮料瓶捆扎在一起,截面如图,如果接头部分用去10厘米,捆扎一圈需要绳子( )厘米。
17.瑞士数学教师巴尔末成功地从光谐数据、、、,…中得到巴尔末公式,从而打开了光谱奥妙的大门,按这种规律写出的第7个数是( )。
三、判断题(每题1分,共5分)
18.聪聪倒了一杯果汁,先喝了10%,加满水搅匀后又喝了20%,再加满水搅匀,又喝了70%,最后加满水喝完.果汁中加的水正好也是1杯.( )
19.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒。( )
20.商家分别以200元的价格卖了两件上衣,其中一件赚了10%,另一件赔了10%.总的来说,商家不赔不赚.( )
21.在含盐20%的盐水中,同时加入200克水和3克盐后,含盐率小于20%。( )
22.一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形。( )
四、计算题(共22分)
23.选择你喜欢的方法计算。(每题2分,共10分)
÷[×(1.056-0.5+0.194)]
24.解方程(每题2分,共6分)
(1)4x-3(20-x)+4=0 (2)
25.求阴影部分面积。(单位:cm,π取3.14)(每题3分,共6分)
(1) (2)
五、作图题(每题1分,共4分)
26.将一个大正方形平均分成四个完全一样的小正方形(如图),请根据下列要求在图上分割.
(1)将空白部分A分成两个形状完全相同的图形.
(2)将空白部分B分成三个形状完全相同的图形.
(3)将空白部分C分成四个形状完全相同的图形.
(4)将空白部分D分成五个形状完全相同的图形.
六、解答题(每题5分,第33题7分,共36分)
27.一条公路,甲队独修24天可以完成,乙队独修30天可以完成。现先由甲、乙两队合修4天,再由丙队参加一起修7天后全部完成。如果三队同时开工修这条路,几天可以完成?
28.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
在一幅比例尺是1∶4500000的地图上,量得两地距离是10厘米。一列客车和一列货车同时从两地相对开出,3小时相遇。已知客车和货车的速度比是3∶2,货车每小时行多少千米?
30.如图所示的四个圆形跑道,每个跑道的长都是1千米,A、B、C、D四位运动员同时从交点O出发,分别沿四个跑道跑步,他们的速度分别是每小时4千米,每小时8千米,每小时6千米,每小时12千米.问从出发到四人再次相遇,四人共跑了多少千米?
(广州)甲、乙、丙三人都要从A地到B地去,甲有一辆摩托车每次只能带一人,甲每小时可以行36千米,乙、丙步行的速度为每小时4千米,已知A、B两地相距36千米.求三人同时到达的最短时间为多少小时?
往返于A、B两地的甲、乙两辆公共汽车分别从A、B两城同时相向出发,各自到达终点停车5分钟便返回出发地,并同时到达C站.已知C站距A、B的中点6千米,甲、乙两辆汽车的速度比是6:5,求AB两城相距多少千米?
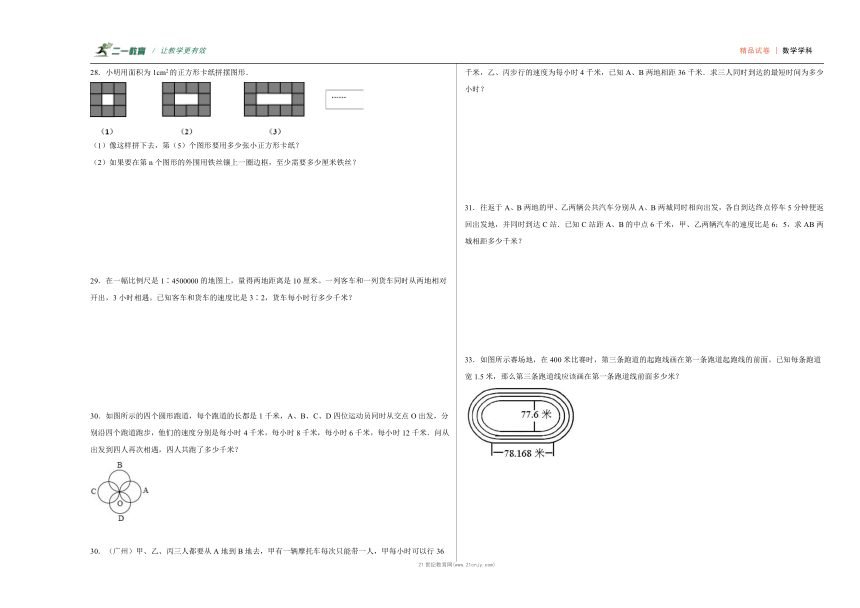
33.如图所示赛场地,在400米比赛时,第三条跑道的起跑线画在第一条跑道起跑线的前面。已知每条跑道宽1.5米,那么第三条跑道线应该画在第一条跑道线前面多少米?
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】要使审核完这些课题的天数尽量的多,每天审核的课题数应该尽量的少。因为每天安排审核的课题个数互不相同且不为零,且1+2+3+4+5+6+7=28,所以可以构造: 1+2+3+4+5+6+9=30 (或者1+2+3+4+5+7+8=30) ,据此解答。
【详解】因为30= 1+2+3+4+5+6+ 9
或30= 1+2+3+4+5+7+8
如果每天审核1,2,3, 4,5,6, 9个,用7天审完;
如果每天审核1、2、3、4、5、7、8个,也用7天审完;
审核完这些课题最多需要7天。
故选择:A
【点睛】每天安排审核的课题个数互不相等且不为0,总课题只有30个,有关部门又是连续审核,按此要求,在最不利的情况下,不妨把每天审的问题个数按从小到大排列如下: 1, 2,3, 4,5,6,7,注意到:1+2+3+4+5+6+7=28,这就用了7天,余下30-28=2 (个)问题,若再用一天或两天,则与前7天中某一天审2个或1个在数量上相等,这与题设矛盾,因此只能在前7天中的某一天中多审2个或某两天各多审1个问题即可,因此最多7天审完。
2.B
【分析】通过树状图观察排列规律可得:第n幅图需要:根小棒,根据规律做题即可。
【详解】第一幅图:(根)
第二幅图:(根)
第三幅图:(根)
第四幅图:(根)
第五幅图:(根)
故答案为:B
【点睛】本题主要考查数与形结合的规律,关键从所给的图形中发现规律,并运用规律做题。
3.A
【详解】2+3=5
2+7=9
2+8=10
3+7=10
3+8=11
7+8=15
4个奇数,2个偶数
故答案为:A
4.C
【分析】可以先假设第一根铁丝的具体长度,从而根据题意求出第一根铁丝的剩余长度,因为两根铁丝剩余长度一样,即可求出第二根铁丝的长度,然后跟第一根铁丝的长度比较大小即可判断原来两根铁丝的长短,通过计算发现结论主要跟假设的铁丝的长度是否是1米有很大关系,从而可以分为大于1米、等于1米、小于1米,三种情况假设即可得到正确结论。
【详解】根据分析:
假设第一根铁丝长2米(大于1),那么第一根铁丝剩下米,那么第二根铁丝的长为米,,则原来第二根铁丝长;假设第一根铁丝长1米,那么第一根铁丝剩下米,那么第二根铁丝长就为米,则两根铁丝原来一样长;假设第一根铁丝长0.9米(小于1),那么第一根铁丝就剩下米,那么第二根铁丝的长为米,,则原来第一根铁丝长;因为题中没有给出第一根铁丝的长度或剩余铁丝的长度,所以两根铁丝原来的长度无法比较。故答案为:C
【点睛】本题主要考查学生能正确区分分数是表示分率还是一个具体的数,学生很容易混淆。
5.D
【分析】根据题意,把“被10除余数是9,被9除余数是8,被8除余数是7”,转化为:每10个分一份,少1,;每9个分一份,少1;每8个分一份,少1。所以求10、9、8的公倍数在100~1000之间的数少1,即可。
【详解】10、9、8的最小公倍数是360,在100~1000之间的倍数有:360,720
360-1=359
720-1=719
所以这个数可能是359,719,这样的数有两个。
故答案为:D
【点睛】本题考查带余除法,关键是把除以一个数余几,转化为少多少,再进行解答。
6.B
【分析】先算出爸爸2万元买3年国债到期的利息,20000×4%×3=2400元,加上本金,20000+2400=22400元;爸爸买理财产品收益:第一年为:20000×4%=800元,本金+利息为:800+20000=20800元;第二年为:20800×4%=832元,本金+利息为:20800+832=21632元;第三年为:21632×4%=865.28元,本金+利息为:21632+865.28=22497.28元;比较22400和22497.28的大小,即可解答问题。
【详解】三年期:10000×4%×3
=400×3
=1200(元)
先买一年期,把本金和利息取出来合在一起,再存入一年,
10000×4%×1=400(元)
(10000+400)×4%×1
=10400×4%×1
=416(元)
(10000+400+416)×4%×1
=10816×4%×1
=432.64(元)
400+416+432.64
=816+432.64
=1248.64(元)
1200<1248.64
买银行1年期理财产品收益更大。
故答案为:B
【点睛】本题考查了利息相关问题,公式:利息=本金×利率×时间。
7.2116
【分析】根据题意可以得到规律:个位数结果为个位数,十位数结果为十位数×个位数,百位数为百位数×个位数.据此规律解决此题即可.
【详解】f(1)+f(2)+f(3)+…+f(99)+f(100)
=(1+2+3…+9)+1×(1+2+3…+9)+2×(1+2+3…+9)+3×(1+2+3…+9)+…+9×(1+2+3…+9)+(1+2+3…+9+1)
=(1+2+3…+9)×(1+1+2+3…+9)+46
=45×46+46
=2116.
故答案为2116.
8. 91.75 92.75 91.75+x 94.75
【详解】思路分析:(1)先求出这四个同学的总成绩,然后根据“总成绩÷人数=平均成绩”进行解答即可;
(2)因为每个同学增加1分,所以平均分增加1分,为91.75+1=92.75分;
(3)因为每个同学增加x分,所以平均分增加x分,为91.75+x分;
(4)因为:100-97=3(分),所以最多每人增加3分,即平均分最多为:91.75+3=94.75分;据此解答即可.
名师详解:(1)(97+92+88+90)÷4,
=367÷4,
=91.75(分);
答:这四个同学的平均分是91.75分;
(2)91.75+1,
=92.75(分);
答:平均分是92.75分;
(3)91.75+x(分);
答:这四人的平均分是91.75+x分;
(4)因为:100-97=3(分),所以最多每人增加3分,即平均分最多为:
91.75+3=94.75(分);
答:平均成绩最多是94.75分;
因而答案为:91.75,92.75,91.75+x,94.75.
易错提示:出错的主要原因就是第四问,若四个同学的成绩增加相同的分数,平均成绩最多是多少分(满分为100分),学生这一问有理解不够清楚的.应该以97分为例,97分和100差3分,所以每个同学都增加3分,平均成绩最多是94.75分.注意的是,此题考查了平均数的含义和计算方法,应理解并能灵活运用.
9.真
【详解】若尼尔斯再次遇到狐狸时是星期四,这天狐狸说的是真话.因此狐狸每星期一、二、三说谎,那么尼尔斯初次遇到狐狸时,狐狸说的是真话,但那么是星期一,狐狸应该说谎话,产生矛盾.故尼尔斯再次遇到狐狸时不是星期四,同样也不应是星期五,星期六.
若尼尔斯再次遇到狐狸时是星期日,这天狐狸说的是真话,三天前是星期四,狐狸说的也应是真话.因此狼说的应该是谎话,但狼说它自己每星期四说谎却成了真话,这不可能.故尼尔斯再次遇到狐狸不是星期日,同样可说明这天也不是星期一和星期二.
因此,尼尔斯再次遇到狐狸时必定是星期三,狐狸说的是真话,初次遇到狐狸是星期日,狐狸说的是谎话,当时狼说的是真话,即狼每星期四、五、六说谎.
故第三天后(星期三),狼说的是真话.
10.502.4
【分析】如图可知,圆柱的侧面积等于侧放后长方体的两个底面积,圆柱的底面半径是侧放后长方体的高,根据长方体的体积公式V=Sh,用一个底面积乘高即是长方体的体积,因为圆柱的体积与长方体的体积相等,所以圆柱的体积也是一个底面积乘高,即圆柱的侧面积的一半乘半径,据此求出圆柱的体积。
【详解】251.2÷2×4
=125.6×4
=502.4(立方厘米)
【点睛】结合图形,找到圆柱的侧面积、半径与长方体的底面积、高的关系是解题的关键。
11.17
【分析】由题意知:每人多分4﹣3=1个草莓,共多需要2+3=5个草莓,这样就可求出分草莓的人数是5÷1=5人,然后根据其中的任一个分配方案即可求出这盘草莓的总个数.
【详解】解:(2+3)÷(4﹣3)=5(人)
3×5+2=17(个)
答:这盘草莓有17个.
此题只要灵活运用“盈亏问题”公式即可解答.
12.150
【分析】把原来的甲车间每人每天的工资看成单位“1”,现在每人每天的工资是原来的1+10%,它对应的数量是60元,由此用除法求出原来甲车间每人每天的工资;再用甲车间每人每天的工资乘原来的人数就是需要发的总工资;工厂每天所发工资总额与以前相同,也就是说各自车间走的人的工资就是增加的工资;所以再用总工资除以后来甲车间每人每天的工资数就是甲车间现在有的人数。
【详解】60÷(1+20%)
=60÷120%
=50(元)
180×50÷60
=9000÷60
=150(人)
即甲车间现有工人150人。
【点睛】本题给出的数据较多,关键是从中找出有用的数据,找出单位“1”,然后再求出不变的总量,然后利用数量之间的关系解决问题。
13.728
【详解】用递推法可知,原来桶中有农药
[(320+80)÷(1-)-120]÷(1-)=728(克).
14.8
【分析】在完成这项工作中,提前3天干完,两人工效相同,则乙帮甲干了3天,所以甲实际工作了(2+3)天,乙帮甲3天干的工作量由甲干也需3天,所以甲计划独自(2+3+3)天干完。
【详解】2+3+3=8(天)
甲志愿者计划完成此项工作的天数是8天。
15.40
【分析】
BF=FC,则BF∶FC=1∶3,△EFB和△EFC的高相等,所以△EFB和△EFC的面积比是1∶3,也就是把△EFC的面积看作3份,△EFB的面积是1份,则△EBC的面积是4份。
AE=CE,则AE∶CE=1∶4,△EBA和△EBC的高相等,所以△EBA和△EBC的面积比是1∶4,也就是把△EBC的面积看作4份,△EBA的面积是1份,△ABC的面积是5份。
【详解】24÷3×(1+3)
=8×4
=32(平方厘米)
32÷4×(1+4)
=8×5
=40(平方厘米)
【点睛】当两个三角形的高相等时,面积之比等于底之比。
16.38.56
【分析】绳子的长度是由三部分组成的,第一部分是接头用去的10厘米;第二部分是瓶身上环绕的绳子长度,在一个瓶身上环绕的绳子长度是这个圆周长的,4个弧线部分合起来正好是一个圆的周长,即3.14×4=12.56(厘米);第三部分是连接两个瓶身圆柱的绳长,每条绳长正好等于两个圆的半径的和,也就是直径的长度,有4条,是4×4=16(厘米),捆扎一圈就是把这三部分加起来。
【详解】10+3.14×4+4×4
=10+12.56+16
=38.56(厘米)
【点睛】关键是看懂图示,掌握圆的周长公式,圆的周长=πd。
17.
【分析】由前面四个数可知,分子是序数与2的和的平方,分母比分子小4,可得第7个数。
【详解】由题目可得:=;=;=;=;
所以第7个数为:=。
【点睛】本题考查了数字排列的规律,关键是要从前面的几个数找出规律从而进行解答。
18.√
【详解】略
19.√
【分析】规律:小棒的根数=小正方形的个数×3+1,根据这样的规律计算后做出判断即可。
【详解】摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
………
所以摆n个正方形要小棒:4+3×(n-1)=3n+1(根);
n=10,3×10+1=31(根);摆10个正方形一共需要31根小棒,原题说法正确。
故答案为:√
20.×
【详解】略
21.√
【分析】200克水和3克盐的含盐率是3÷(200+3)×100%≈1.4%,与20%的盐水混合,相当于稀释了,因此混合后盐水的含盐率小于20%。
【详解】3÷(200+3)×100%≈1.4%
1.4%<20%,因此混合后含盐率小于20%。
故答案为:√
【点睛】此题主要考查了含盐率的求法,要熟练掌握。
22.√
【分析】圆锥纵切面是一个三角形,三角形的底是圆锥底面直径,三角形高是圆锥的高,如果圆锥的底面半径和高相等,纵切面如图,切面是一个等腰直角三角形。
【详解】根据分析,一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形,说法正确。
故答案为:√
【点睛】关键是熟悉圆锥特征,想清楚纵切面和圆锥之间的关系。
23.;6
20.07;
【分析】÷[×(1.056-0.5+0.194)],根据加法交换律,把小括号的式子化为:1.056+0.194-0.5,原式化为:÷[×(1.056+0.194-0.5)],再按照运算顺序,先计算小括号里的加法,再计算小括号里的减法,接着计算中括号里的乘法,最后计算括号外的除法;
×2.6+×2.2,把带分数化成假分数,=,原式化为:×2.6+×2.2,再把12化为6×2,原式化为:×2.6+×2.2,把化为×2,原式化为:×2.6+×2×2.2,再根据乘法分配律逆运算,原式化为:×(2.6+2×2.2),再进行计算;
20.07×1994-19.93×2007,把19.93×2007化为1993×20.07,原式化为:20.07×1994-1993×20.07,再根据乘法分配律逆运算,原式化为:20.07×(1994-1993),再进行计算;
÷[(+)×],先计算小括号里的加法,再加上中括号里乘法,最后计算括号外的除法;
(1+++++)÷(+++++),把1+++++化为分母是30的分数,原式化为:+++++,把+++++化为分母为60的分数,原式化为:+++++;原式化为:(+++++)÷(+++++);根据乘法分配律逆运算,原式化为:[×(30+10+6+3+2+1)]÷[×(30+15+10+5+3+1)],再进行计算。
【详解】÷[×(1.056-0.5+0.194)]
=÷[×(1.056+0.194-0.5)]
==÷[×(1.25-0.5)]
=÷[×0.75]
=÷[×]
=÷
=×
=
×2.6+×2.2
=×2.6+×2.2
=×2.6+×2.2
=×2.6+×2×2.2
=×(2.6+2×2.2)
=×(2.6+4.4)
=×7
=6
20.07×1994-19.93×2007
=20.07×1994-1993×20.07
=20.07×(1994-1993)
=20.07×1
=20.07
÷[(+)×]
=÷[(+)×]
=÷[×]
=÷
=×2
=
(1+++++)÷(+++++)
=(+++++)÷(+++++)
=[×(30+10+6+3+2+1)]÷[×(30+15+10+5+3+1)]
=[×(40+6+3+2+1)]÷[×(45+10+5+3+1)]
=[×(46+3+2+1)]÷[×(55+5+3+1)]
=[×(49+2+1)]÷[×(60+3+1)]
=[×52]÷[×(63+1)]
=÷[×64]
=÷
=×
=
24.x=8;x=4.5
【分析】(1)先用乘法分配律计算3(20-x)=3×20-3x=60-3x,再利用减法的性质去掉括号,然后将带x的数用小括号括起来计算(4x+3x),另外两个数运用减法的性质使用小括号括起来计算(60-4),接着将方程左右两边同时加上两个数计算出的结果60-4=56,最后方程左右两边同时除以7即可;
(2)先将方程左右两边同时加上,将方程右边的算式通分计算,方程左右两边同时乘6,运用乘法分配律计算方程右边的算式,利用减法的性质计算分子部分带x的算式,接着方程左右两边同时加上4x,再同时减去6,最后方程左右两边同时除以4即可;据此解答。
【详解】(1)4x-3(20-x)+4=0
解:4x-(3×20-3x)+4=0
4x-60+3x+4=0
(4x+3x)-(60-4)=0
7x-56=0
7x-56+56=0+56
7x÷7=56÷7
x=8
(2)
解:
6=24-6x+2x
6=24-(6x-2x)
6=24-4x
6+4x=24-4x+4x
6+4x-6=24-6
4x÷4=18÷4
x=4.5
25.(1)16平方厘米;(2)22平方厘米
【分析】(1)将右半部分的不规则阴影部分绕圆心顺时针旋转90°然后再平移,阴影部分的面积相当于底是8厘米、高是4厘米的平行四边形面积的一半,根据平行四边形的面积公式:平行四边形的面积=底×高,用8×(8÷2)÷2即可求出阴影部分的面积。
(2)将左上部分阴影填补到中间空白处,那么阴影部分的面积恰好是上底为4,下底为7,高为4的梯形的面积,梯形的面积=(上底+下底)×高÷2。
【详解】(1)8×4÷2
=32÷2
=16(平方厘米)
阴影部分的面积是16平方厘米。
(2)(4+7)×4÷2
=44÷2
=22(平方厘米)
阴影部分的面积是22平方厘米。
26.
【分析】本题考查了图形的划分,关键是将空白部分C分成四个形状完全相同的图形,要先把空白部分C看作是由三个小正方形拼成的,平均分成12个大小相同的小正方形后再组合成四个形状完全相同的图形.
【详解】解:根据分析画图如下:
(1)将空白部分A分成两个形状完全相同的图形,连接左上右下的两个直角顶点即可.
(2)将空白部分B分成三个形状完全相同的图形,连接原来小正方形的两组对边的中点即可.
(3)将空白部分C分成四个形状完全相同的图形,先把空白部分C平均分成12个大小相同的小正方形,再根据它们的位置连成4个大小相同的图形即可.
(4)将空白部分D分成五个形状完全相同的图形,把空白部分D平均分成5个小长方形即可
27.10天
【分析】先根据工作效率=工作总量÷工作时间,求出甲队的工作效率和乙队的工作效率;再求出甲、乙合作4天完成的工作量;然后求出三队合修每天完成的工作量;最后用工作总量除以三队合修的工作效率和就是完成的工作时间,据此解答即可。
【详解】1÷24=
1÷30=
=
=
=
由分析可得:
=
=
(天)
答:10天可以完成。
【点睛】本题考查了工程问题的计算,理解工作总量、工作效率、工作时间的关系可解答问题。
28.(1)16张;(2)(10+2n)厘米.
【详解】(1)由图可知:第(1)个图形的小正方形卡纸个数为3×3-1,第(2)个图形的个数为3×4-2,第(3)个图形的个数为3×5-3,像这样拼下去,第(5)个图形用3×7-5=16张小正方形卡纸.
(2)第n个图形周长=(3+2+n)×2=10+2n(厘米)
29.60千米
【分析】先根据实际距离=图上距离÷比例尺,求出两地的实际距离;然后根据相遇问题中“速度和=相遇路程÷相遇时间”,求出两车的速度和;又已知客车和货车的速度比是3∶2,可知货车的速度占两车速度和的,用两车的速度和乘,求出货车每小时行的路程。
【详解】10÷=45000000(厘米)
45000000厘米=450千米
两车每小时共行:450÷3=150(千米)
货车每小时行:150×=60(千米)
答:货车每小时行60千米。
【点睛】掌握图上距离、实际距离、比例尺之间的关系,以及路程、速度、时间之间的关系和按比例分配是解题的关键。
30.15千米
【分析】首先求出每一个人跑一圈所用的时间,再求出时间的最小公倍数,最后求出在相同的时间内每一个人所跑的圈数,由此解决问题.此题主要考查利用求分数最小公倍数的方法解决问题.
【详解】A跑1圈需要小时,B跑1圈需要小时,C跑1圈需要小时,D跑1圈需要小时;
,,,的最小公倍数是;
也就是说小时后他们四人再次相遇,
此时四人共跑了×(4+8+6+12)=15(千米);
答:从出发到四人再次相遇,四人共跑了15千米.
31.三人同时到达的最短时间为小时
【详解】试题分析:若甲先骑摩托车带乙前行,到达某处后,放下乙,返回接丙,然后带丙前行,与乙同时到达B地:设甲乙先行了x小时,则甲乙行程为36x,丙行程为4x,甲乙,和丙相距:36x﹣4x=32x,甲丙相遇,需要:32x÷(36+4)=x小时,此时,乙和丙各自步行了:4×x=x千米;甲丙,与乙的距离还是32x,三人同时到达,即甲丙正好追上乙,据此即可解答问题.
解答:解:甲先骑摩托车带乙前行,到达某处后,放下乙,返回接丙,然后带丙前行,与乙同时到达B地.
设甲乙先行了x小时,则甲乙行程为36x,丙行程为4x,
甲乙,和丙相距:36x﹣4x=32x,
那么甲丙相遇,需要:32x÷(36+4)=x(小时)
此时,乙和丙各自步行了:4×x=x(千米)
甲丙,与乙的距离还是32x
三人同时到达,即甲丙正好追上乙,需要:
32x÷(36﹣4)=x(小时)
乙或丙的行程,就等于全程,以乙为例,列方程如下:
36x+x+4x=36
x=36
x=
所以最短用时:
x+x+x=x=×=(小时)
答:三人同时到达的最短时间为小时.
点评:此题较复杂,应抓住甲乙丙三人行驶的时间、路程以及他们各自间的距离关系这个关键,进而分析解答即可.
32.44千米
【详解】试题分析:设AB两城相距s千米,从开始到到达C站所用时间为t,到达C站时,甲走的路程为(1.5s+6)千米,乙走的路程为(1.5s﹣6)千米,根据甲、乙两辆汽车的速度比是6:5,列式解答即可.
解:设AB两城相距s千米,从开始到到达C站所用时间为t,
5(1.5s+6)=6(1.5s﹣6)
7.5s+30=9s﹣36
30+36=9s﹣7.5s
66=1.5s
s=44,
答:AB两城相距44千米.
点评:本题考查了简单的行程问题以及比的应用.关键是得出到达C站时,甲走的路程为(1.5s+6)千米,乙走的路程为(1.5s﹣6)千米.
33.6π米
【分析】要求第三条跑道应该画在第一条跑道线前面多少米时,直线跑道的长度不变,可以不考虑,只需要考虑直径第三条跑道比第一条跑道之间环宽差,用它们之间的环宽差乘2再乘圆周率即可。
【详解】1.5×2×3=9(米)
1.5×2=3(米)
(9-3)π=6π(米)
答:第三条跑道线应该画在第一条跑道线前面6π米处。
【点睛】本题考查了圆的周长,圆的周长=2πr。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(每题2分,共12分)
1.有关部门要连续审核30个科研课题方案,如果要求每天安排审核的课题个数互不相等且不为零,则审核完这些课题最多需要( )。
A.7天 B.8天 C.9天 D.10天
2.红红按照一定的规律用小棒摆出了下面的4幅图。
如果按照这个规律继续摆,第五幅图要用( )根小棒。
A.23 B.31 C.35 D.45
3.将分别写有2,3,7,8四个数字的二张卡片反扣在桌面上,任意抽两张,和是奇数的可能性 和是偶数的可能性。
A.大于 B.小于 C.等于 D.无法确定
4.有两根铁丝,第一根用去米,第二根用去,剩下的一样长,两根铁丝原来相比( )。
A.第一根长 B.一样长 C.无法确定
5.某S为自然数,被10除余数是9,被9除余数是8,被8除余数是7,已知100<S<1000,请问这样的数有几个?( )
A.5 B.4 C.3 D.2
6.爸爸有2万元钱,有两种理财方式:一种是买3年期国债,年利率为4%;另一种是买银行1年期理财产品,年收益率是4%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大( )。
A.国债 B.理财产品 C.一样大 D.无法确定
二、填空题(每空1.5分,共21分)
7.用f(n)表示组成n的数字中不是零的几个数字乘积,例如:f(5)=5;f(29)=18; f(207)=14.则f(1)+f(2)+f(3)+…+f(99)+f(100)=( ).
8.A、B、C、D四个同学在一次数学考试中的成绩分别为97分、92分、88分和90分.这四个同学的平均分是( )分;若每个同学增加1分,平均分是( )分;若每个同学增加X分,那么这四人的平均分是( )分;若四个同学的成绩增加相同的分数,平均成绩最多是( )分(满分为100分)
9.尼尔斯在骑鹅旅行时来到一个小岛上,这里不论是谁,每星期都有几天说真话,有几天则说假话.有一天,尼尔斯遇到狐狸和狼,狐狸说:“每星期一、二、三是我说谎的日子.”而狼说:“每星期四、五、六是我说谎的日子,刚才狐狸说的不是真话!”三天后,尼尔斯又遇到它们,他已经知道这天狐狸说的是真话,这天狼说的是( )话.
10.聪聪在探究圆柱体积时,先把圆柱体拼成一个近似长方体,再把这个长方体侧放,他发现了一种更巧妙的方法(如图)。如果圆柱的底面半径是4厘米,侧面积是251.2平方厘米,这个圆柱的体积是( )立方厘米。
11.一盘草莓约20个左右,几位小朋友分.若每人分3个,则余下2个;若每人分4个,则差3个.这盘草莓有( )个.
12.某厂甲车间有工人180人,乙车间有工人120人,现从两车间共调出50名工人支援新厂,余下工人因工作量增加,每人每天增加工资20%,因工种不同,甲车间工人每人每天工资60元,乙车间工人每人每天工资48元,已知工厂每天所发工资总额与以前相同,甲车间现有工人( )人。
13.一桶农药,第一次倒出2/7然后倒回桶内120克,第二次倒出桶中剩下农药的3/8,第三次倒出320克,桶中还剩下80克,原来桶中有农药( )克.
14.甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲志愿者计划完成此项工作的天数是( )天。
15.如图,三角形EFC的面积是24平方厘米,AE=CE,BF=FC,则三角形ABC的面积为( )平方厘米。
16.把4个直径是4厘米的圆柱形饮料瓶捆扎在一起,截面如图,如果接头部分用去10厘米,捆扎一圈需要绳子( )厘米。
17.瑞士数学教师巴尔末成功地从光谐数据、、、,…中得到巴尔末公式,从而打开了光谱奥妙的大门,按这种规律写出的第7个数是( )。
三、判断题(每题1分,共5分)
18.聪聪倒了一杯果汁,先喝了10%,加满水搅匀后又喝了20%,再加满水搅匀,又喝了70%,最后加满水喝完.果汁中加的水正好也是1杯.( )
19.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒。( )
20.商家分别以200元的价格卖了两件上衣,其中一件赚了10%,另一件赔了10%.总的来说,商家不赔不赚.( )
21.在含盐20%的盐水中,同时加入200克水和3克盐后,含盐率小于20%。( )
22.一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形。( )
四、计算题(共22分)
23.选择你喜欢的方法计算。(每题2分,共10分)
÷[×(1.056-0.5+0.194)]
24.解方程(每题2分,共6分)
(1)4x-3(20-x)+4=0 (2)
25.求阴影部分面积。(单位:cm,π取3.14)(每题3分,共6分)
(1) (2)
五、作图题(每题1分,共4分)
26.将一个大正方形平均分成四个完全一样的小正方形(如图),请根据下列要求在图上分割.
(1)将空白部分A分成两个形状完全相同的图形.
(2)将空白部分B分成三个形状完全相同的图形.
(3)将空白部分C分成四个形状完全相同的图形.
(4)将空白部分D分成五个形状完全相同的图形.
六、解答题(每题5分,第33题7分,共36分)
27.一条公路,甲队独修24天可以完成,乙队独修30天可以完成。现先由甲、乙两队合修4天,再由丙队参加一起修7天后全部完成。如果三队同时开工修这条路,几天可以完成?
28.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
在一幅比例尺是1∶4500000的地图上,量得两地距离是10厘米。一列客车和一列货车同时从两地相对开出,3小时相遇。已知客车和货车的速度比是3∶2,货车每小时行多少千米?
30.如图所示的四个圆形跑道,每个跑道的长都是1千米,A、B、C、D四位运动员同时从交点O出发,分别沿四个跑道跑步,他们的速度分别是每小时4千米,每小时8千米,每小时6千米,每小时12千米.问从出发到四人再次相遇,四人共跑了多少千米?
(广州)甲、乙、丙三人都要从A地到B地去,甲有一辆摩托车每次只能带一人,甲每小时可以行36千米,乙、丙步行的速度为每小时4千米,已知A、B两地相距36千米.求三人同时到达的最短时间为多少小时?
往返于A、B两地的甲、乙两辆公共汽车分别从A、B两城同时相向出发,各自到达终点停车5分钟便返回出发地,并同时到达C站.已知C站距A、B的中点6千米,甲、乙两辆汽车的速度比是6:5,求AB两城相距多少千米?
33.如图所示赛场地,在400米比赛时,第三条跑道的起跑线画在第一条跑道起跑线的前面。已知每条跑道宽1.5米,那么第三条跑道线应该画在第一条跑道线前面多少米?
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】要使审核完这些课题的天数尽量的多,每天审核的课题数应该尽量的少。因为每天安排审核的课题个数互不相同且不为零,且1+2+3+4+5+6+7=28,所以可以构造: 1+2+3+4+5+6+9=30 (或者1+2+3+4+5+7+8=30) ,据此解答。
【详解】因为30= 1+2+3+4+5+6+ 9
或30= 1+2+3+4+5+7+8
如果每天审核1,2,3, 4,5,6, 9个,用7天审完;
如果每天审核1、2、3、4、5、7、8个,也用7天审完;
审核完这些课题最多需要7天。
故选择:A
【点睛】每天安排审核的课题个数互不相等且不为0,总课题只有30个,有关部门又是连续审核,按此要求,在最不利的情况下,不妨把每天审的问题个数按从小到大排列如下: 1, 2,3, 4,5,6,7,注意到:1+2+3+4+5+6+7=28,这就用了7天,余下30-28=2 (个)问题,若再用一天或两天,则与前7天中某一天审2个或1个在数量上相等,这与题设矛盾,因此只能在前7天中的某一天中多审2个或某两天各多审1个问题即可,因此最多7天审完。
2.B
【分析】通过树状图观察排列规律可得:第n幅图需要:根小棒,根据规律做题即可。
【详解】第一幅图:(根)
第二幅图:(根)
第三幅图:(根)
第四幅图:(根)
第五幅图:(根)
故答案为:B
【点睛】本题主要考查数与形结合的规律,关键从所给的图形中发现规律,并运用规律做题。
3.A
【详解】2+3=5
2+7=9
2+8=10
3+7=10
3+8=11
7+8=15
4个奇数,2个偶数
故答案为:A
4.C
【分析】可以先假设第一根铁丝的具体长度,从而根据题意求出第一根铁丝的剩余长度,因为两根铁丝剩余长度一样,即可求出第二根铁丝的长度,然后跟第一根铁丝的长度比较大小即可判断原来两根铁丝的长短,通过计算发现结论主要跟假设的铁丝的长度是否是1米有很大关系,从而可以分为大于1米、等于1米、小于1米,三种情况假设即可得到正确结论。
【详解】根据分析:
假设第一根铁丝长2米(大于1),那么第一根铁丝剩下米,那么第二根铁丝的长为米,,则原来第二根铁丝长;假设第一根铁丝长1米,那么第一根铁丝剩下米,那么第二根铁丝长就为米,则两根铁丝原来一样长;假设第一根铁丝长0.9米(小于1),那么第一根铁丝就剩下米,那么第二根铁丝的长为米,,则原来第一根铁丝长;因为题中没有给出第一根铁丝的长度或剩余铁丝的长度,所以两根铁丝原来的长度无法比较。故答案为:C
【点睛】本题主要考查学生能正确区分分数是表示分率还是一个具体的数,学生很容易混淆。
5.D
【分析】根据题意,把“被10除余数是9,被9除余数是8,被8除余数是7”,转化为:每10个分一份,少1,;每9个分一份,少1;每8个分一份,少1。所以求10、9、8的公倍数在100~1000之间的数少1,即可。
【详解】10、9、8的最小公倍数是360,在100~1000之间的倍数有:360,720
360-1=359
720-1=719
所以这个数可能是359,719,这样的数有两个。
故答案为:D
【点睛】本题考查带余除法,关键是把除以一个数余几,转化为少多少,再进行解答。
6.B
【分析】先算出爸爸2万元买3年国债到期的利息,20000×4%×3=2400元,加上本金,20000+2400=22400元;爸爸买理财产品收益:第一年为:20000×4%=800元,本金+利息为:800+20000=20800元;第二年为:20800×4%=832元,本金+利息为:20800+832=21632元;第三年为:21632×4%=865.28元,本金+利息为:21632+865.28=22497.28元;比较22400和22497.28的大小,即可解答问题。
【详解】三年期:10000×4%×3
=400×3
=1200(元)
先买一年期,把本金和利息取出来合在一起,再存入一年,
10000×4%×1=400(元)
(10000+400)×4%×1
=10400×4%×1
=416(元)
(10000+400+416)×4%×1
=10816×4%×1
=432.64(元)
400+416+432.64
=816+432.64
=1248.64(元)
1200<1248.64
买银行1年期理财产品收益更大。
故答案为:B
【点睛】本题考查了利息相关问题,公式:利息=本金×利率×时间。
7.2116
【分析】根据题意可以得到规律:个位数结果为个位数,十位数结果为十位数×个位数,百位数为百位数×个位数.据此规律解决此题即可.
【详解】f(1)+f(2)+f(3)+…+f(99)+f(100)
=(1+2+3…+9)+1×(1+2+3…+9)+2×(1+2+3…+9)+3×(1+2+3…+9)+…+9×(1+2+3…+9)+(1+2+3…+9+1)
=(1+2+3…+9)×(1+1+2+3…+9)+46
=45×46+46
=2116.
故答案为2116.
8. 91.75 92.75 91.75+x 94.75
【详解】思路分析:(1)先求出这四个同学的总成绩,然后根据“总成绩÷人数=平均成绩”进行解答即可;
(2)因为每个同学增加1分,所以平均分增加1分,为91.75+1=92.75分;
(3)因为每个同学增加x分,所以平均分增加x分,为91.75+x分;
(4)因为:100-97=3(分),所以最多每人增加3分,即平均分最多为:91.75+3=94.75分;据此解答即可.
名师详解:(1)(97+92+88+90)÷4,
=367÷4,
=91.75(分);
答:这四个同学的平均分是91.75分;
(2)91.75+1,
=92.75(分);
答:平均分是92.75分;
(3)91.75+x(分);
答:这四人的平均分是91.75+x分;
(4)因为:100-97=3(分),所以最多每人增加3分,即平均分最多为:
91.75+3=94.75(分);
答:平均成绩最多是94.75分;
因而答案为:91.75,92.75,91.75+x,94.75.
易错提示:出错的主要原因就是第四问,若四个同学的成绩增加相同的分数,平均成绩最多是多少分(满分为100分),学生这一问有理解不够清楚的.应该以97分为例,97分和100差3分,所以每个同学都增加3分,平均成绩最多是94.75分.注意的是,此题考查了平均数的含义和计算方法,应理解并能灵活运用.
9.真
【详解】若尼尔斯再次遇到狐狸时是星期四,这天狐狸说的是真话.因此狐狸每星期一、二、三说谎,那么尼尔斯初次遇到狐狸时,狐狸说的是真话,但那么是星期一,狐狸应该说谎话,产生矛盾.故尼尔斯再次遇到狐狸时不是星期四,同样也不应是星期五,星期六.
若尼尔斯再次遇到狐狸时是星期日,这天狐狸说的是真话,三天前是星期四,狐狸说的也应是真话.因此狼说的应该是谎话,但狼说它自己每星期四说谎却成了真话,这不可能.故尼尔斯再次遇到狐狸不是星期日,同样可说明这天也不是星期一和星期二.
因此,尼尔斯再次遇到狐狸时必定是星期三,狐狸说的是真话,初次遇到狐狸是星期日,狐狸说的是谎话,当时狼说的是真话,即狼每星期四、五、六说谎.
故第三天后(星期三),狼说的是真话.
10.502.4
【分析】如图可知,圆柱的侧面积等于侧放后长方体的两个底面积,圆柱的底面半径是侧放后长方体的高,根据长方体的体积公式V=Sh,用一个底面积乘高即是长方体的体积,因为圆柱的体积与长方体的体积相等,所以圆柱的体积也是一个底面积乘高,即圆柱的侧面积的一半乘半径,据此求出圆柱的体积。
【详解】251.2÷2×4
=125.6×4
=502.4(立方厘米)
【点睛】结合图形,找到圆柱的侧面积、半径与长方体的底面积、高的关系是解题的关键。
11.17
【分析】由题意知:每人多分4﹣3=1个草莓,共多需要2+3=5个草莓,这样就可求出分草莓的人数是5÷1=5人,然后根据其中的任一个分配方案即可求出这盘草莓的总个数.
【详解】解:(2+3)÷(4﹣3)=5(人)
3×5+2=17(个)
答:这盘草莓有17个.
此题只要灵活运用“盈亏问题”公式即可解答.
12.150
【分析】把原来的甲车间每人每天的工资看成单位“1”,现在每人每天的工资是原来的1+10%,它对应的数量是60元,由此用除法求出原来甲车间每人每天的工资;再用甲车间每人每天的工资乘原来的人数就是需要发的总工资;工厂每天所发工资总额与以前相同,也就是说各自车间走的人的工资就是增加的工资;所以再用总工资除以后来甲车间每人每天的工资数就是甲车间现在有的人数。
【详解】60÷(1+20%)
=60÷120%
=50(元)
180×50÷60
=9000÷60
=150(人)
即甲车间现有工人150人。
【点睛】本题给出的数据较多,关键是从中找出有用的数据,找出单位“1”,然后再求出不变的总量,然后利用数量之间的关系解决问题。
13.728
【详解】用递推法可知,原来桶中有农药
[(320+80)÷(1-)-120]÷(1-)=728(克).
14.8
【分析】在完成这项工作中,提前3天干完,两人工效相同,则乙帮甲干了3天,所以甲实际工作了(2+3)天,乙帮甲3天干的工作量由甲干也需3天,所以甲计划独自(2+3+3)天干完。
【详解】2+3+3=8(天)
甲志愿者计划完成此项工作的天数是8天。
15.40
【分析】
BF=FC,则BF∶FC=1∶3,△EFB和△EFC的高相等,所以△EFB和△EFC的面积比是1∶3,也就是把△EFC的面积看作3份,△EFB的面积是1份,则△EBC的面积是4份。
AE=CE,则AE∶CE=1∶4,△EBA和△EBC的高相等,所以△EBA和△EBC的面积比是1∶4,也就是把△EBC的面积看作4份,△EBA的面积是1份,△ABC的面积是5份。
【详解】24÷3×(1+3)
=8×4
=32(平方厘米)
32÷4×(1+4)
=8×5
=40(平方厘米)
【点睛】当两个三角形的高相等时,面积之比等于底之比。
16.38.56
【分析】绳子的长度是由三部分组成的,第一部分是接头用去的10厘米;第二部分是瓶身上环绕的绳子长度,在一个瓶身上环绕的绳子长度是这个圆周长的,4个弧线部分合起来正好是一个圆的周长,即3.14×4=12.56(厘米);第三部分是连接两个瓶身圆柱的绳长,每条绳长正好等于两个圆的半径的和,也就是直径的长度,有4条,是4×4=16(厘米),捆扎一圈就是把这三部分加起来。
【详解】10+3.14×4+4×4
=10+12.56+16
=38.56(厘米)
【点睛】关键是看懂图示,掌握圆的周长公式,圆的周长=πd。
17.
【分析】由前面四个数可知,分子是序数与2的和的平方,分母比分子小4,可得第7个数。
【详解】由题目可得:=;=;=;=;
所以第7个数为:=。
【点睛】本题考查了数字排列的规律,关键是要从前面的几个数找出规律从而进行解答。
18.√
【详解】略
19.√
【分析】规律:小棒的根数=小正方形的个数×3+1,根据这样的规律计算后做出判断即可。
【详解】摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
………
所以摆n个正方形要小棒:4+3×(n-1)=3n+1(根);
n=10,3×10+1=31(根);摆10个正方形一共需要31根小棒,原题说法正确。
故答案为:√
20.×
【详解】略
21.√
【分析】200克水和3克盐的含盐率是3÷(200+3)×100%≈1.4%,与20%的盐水混合,相当于稀释了,因此混合后盐水的含盐率小于20%。
【详解】3÷(200+3)×100%≈1.4%
1.4%<20%,因此混合后含盐率小于20%。
故答案为:√
【点睛】此题主要考查了含盐率的求法,要熟练掌握。
22.√
【分析】圆锥纵切面是一个三角形,三角形的底是圆锥底面直径,三角形高是圆锥的高,如果圆锥的底面半径和高相等,纵切面如图,切面是一个等腰直角三角形。
【详解】根据分析,一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形,说法正确。
故答案为:√
【点睛】关键是熟悉圆锥特征,想清楚纵切面和圆锥之间的关系。
23.;6
20.07;
【分析】÷[×(1.056-0.5+0.194)],根据加法交换律,把小括号的式子化为:1.056+0.194-0.5,原式化为:÷[×(1.056+0.194-0.5)],再按照运算顺序,先计算小括号里的加法,再计算小括号里的减法,接着计算中括号里的乘法,最后计算括号外的除法;
×2.6+×2.2,把带分数化成假分数,=,原式化为:×2.6+×2.2,再把12化为6×2,原式化为:×2.6+×2.2,把化为×2,原式化为:×2.6+×2×2.2,再根据乘法分配律逆运算,原式化为:×(2.6+2×2.2),再进行计算;
20.07×1994-19.93×2007,把19.93×2007化为1993×20.07,原式化为:20.07×1994-1993×20.07,再根据乘法分配律逆运算,原式化为:20.07×(1994-1993),再进行计算;
÷[(+)×],先计算小括号里的加法,再加上中括号里乘法,最后计算括号外的除法;
(1+++++)÷(+++++),把1+++++化为分母是30的分数,原式化为:+++++,把+++++化为分母为60的分数,原式化为:+++++;原式化为:(+++++)÷(+++++);根据乘法分配律逆运算,原式化为:[×(30+10+6+3+2+1)]÷[×(30+15+10+5+3+1)],再进行计算。
【详解】÷[×(1.056-0.5+0.194)]
=÷[×(1.056+0.194-0.5)]
==÷[×(1.25-0.5)]
=÷[×0.75]
=÷[×]
=÷
=×
=
×2.6+×2.2
=×2.6+×2.2
=×2.6+×2.2
=×2.6+×2×2.2
=×(2.6+2×2.2)
=×(2.6+4.4)
=×7
=6
20.07×1994-19.93×2007
=20.07×1994-1993×20.07
=20.07×(1994-1993)
=20.07×1
=20.07
÷[(+)×]
=÷[(+)×]
=÷[×]
=÷
=×2
=
(1+++++)÷(+++++)
=(+++++)÷(+++++)
=[×(30+10+6+3+2+1)]÷[×(30+15+10+5+3+1)]
=[×(40+6+3+2+1)]÷[×(45+10+5+3+1)]
=[×(46+3+2+1)]÷[×(55+5+3+1)]
=[×(49+2+1)]÷[×(60+3+1)]
=[×52]÷[×(63+1)]
=÷[×64]
=÷
=×
=
24.x=8;x=4.5
【分析】(1)先用乘法分配律计算3(20-x)=3×20-3x=60-3x,再利用减法的性质去掉括号,然后将带x的数用小括号括起来计算(4x+3x),另外两个数运用减法的性质使用小括号括起来计算(60-4),接着将方程左右两边同时加上两个数计算出的结果60-4=56,最后方程左右两边同时除以7即可;
(2)先将方程左右两边同时加上,将方程右边的算式通分计算,方程左右两边同时乘6,运用乘法分配律计算方程右边的算式,利用减法的性质计算分子部分带x的算式,接着方程左右两边同时加上4x,再同时减去6,最后方程左右两边同时除以4即可;据此解答。
【详解】(1)4x-3(20-x)+4=0
解:4x-(3×20-3x)+4=0
4x-60+3x+4=0
(4x+3x)-(60-4)=0
7x-56=0
7x-56+56=0+56
7x÷7=56÷7
x=8
(2)
解:
6=24-6x+2x
6=24-(6x-2x)
6=24-4x
6+4x=24-4x+4x
6+4x-6=24-6
4x÷4=18÷4
x=4.5
25.(1)16平方厘米;(2)22平方厘米
【分析】(1)将右半部分的不规则阴影部分绕圆心顺时针旋转90°然后再平移,阴影部分的面积相当于底是8厘米、高是4厘米的平行四边形面积的一半,根据平行四边形的面积公式:平行四边形的面积=底×高,用8×(8÷2)÷2即可求出阴影部分的面积。
(2)将左上部分阴影填补到中间空白处,那么阴影部分的面积恰好是上底为4,下底为7,高为4的梯形的面积,梯形的面积=(上底+下底)×高÷2。
【详解】(1)8×4÷2
=32÷2
=16(平方厘米)
阴影部分的面积是16平方厘米。
(2)(4+7)×4÷2
=44÷2
=22(平方厘米)
阴影部分的面积是22平方厘米。
26.
【分析】本题考查了图形的划分,关键是将空白部分C分成四个形状完全相同的图形,要先把空白部分C看作是由三个小正方形拼成的,平均分成12个大小相同的小正方形后再组合成四个形状完全相同的图形.
【详解】解:根据分析画图如下:
(1)将空白部分A分成两个形状完全相同的图形,连接左上右下的两个直角顶点即可.
(2)将空白部分B分成三个形状完全相同的图形,连接原来小正方形的两组对边的中点即可.
(3)将空白部分C分成四个形状完全相同的图形,先把空白部分C平均分成12个大小相同的小正方形,再根据它们的位置连成4个大小相同的图形即可.
(4)将空白部分D分成五个形状完全相同的图形,把空白部分D平均分成5个小长方形即可
27.10天
【分析】先根据工作效率=工作总量÷工作时间,求出甲队的工作效率和乙队的工作效率;再求出甲、乙合作4天完成的工作量;然后求出三队合修每天完成的工作量;最后用工作总量除以三队合修的工作效率和就是完成的工作时间,据此解答即可。
【详解】1÷24=
1÷30=
=
=
=
由分析可得:
=
=
(天)
答:10天可以完成。
【点睛】本题考查了工程问题的计算,理解工作总量、工作效率、工作时间的关系可解答问题。
28.(1)16张;(2)(10+2n)厘米.
【详解】(1)由图可知:第(1)个图形的小正方形卡纸个数为3×3-1,第(2)个图形的个数为3×4-2,第(3)个图形的个数为3×5-3,像这样拼下去,第(5)个图形用3×7-5=16张小正方形卡纸.
(2)第n个图形周长=(3+2+n)×2=10+2n(厘米)
29.60千米
【分析】先根据实际距离=图上距离÷比例尺,求出两地的实际距离;然后根据相遇问题中“速度和=相遇路程÷相遇时间”,求出两车的速度和;又已知客车和货车的速度比是3∶2,可知货车的速度占两车速度和的,用两车的速度和乘,求出货车每小时行的路程。
【详解】10÷=45000000(厘米)
45000000厘米=450千米
两车每小时共行:450÷3=150(千米)
货车每小时行:150×=60(千米)
答:货车每小时行60千米。
【点睛】掌握图上距离、实际距离、比例尺之间的关系,以及路程、速度、时间之间的关系和按比例分配是解题的关键。
30.15千米
【分析】首先求出每一个人跑一圈所用的时间,再求出时间的最小公倍数,最后求出在相同的时间内每一个人所跑的圈数,由此解决问题.此题主要考查利用求分数最小公倍数的方法解决问题.
【详解】A跑1圈需要小时,B跑1圈需要小时,C跑1圈需要小时,D跑1圈需要小时;
,,,的最小公倍数是;
也就是说小时后他们四人再次相遇,
此时四人共跑了×(4+8+6+12)=15(千米);
答:从出发到四人再次相遇,四人共跑了15千米.
31.三人同时到达的最短时间为小时
【详解】试题分析:若甲先骑摩托车带乙前行,到达某处后,放下乙,返回接丙,然后带丙前行,与乙同时到达B地:设甲乙先行了x小时,则甲乙行程为36x,丙行程为4x,甲乙,和丙相距:36x﹣4x=32x,甲丙相遇,需要:32x÷(36+4)=x小时,此时,乙和丙各自步行了:4×x=x千米;甲丙,与乙的距离还是32x,三人同时到达,即甲丙正好追上乙,据此即可解答问题.
解答:解:甲先骑摩托车带乙前行,到达某处后,放下乙,返回接丙,然后带丙前行,与乙同时到达B地.
设甲乙先行了x小时,则甲乙行程为36x,丙行程为4x,
甲乙,和丙相距:36x﹣4x=32x,
那么甲丙相遇,需要:32x÷(36+4)=x(小时)
此时,乙和丙各自步行了:4×x=x(千米)
甲丙,与乙的距离还是32x
三人同时到达,即甲丙正好追上乙,需要:
32x÷(36﹣4)=x(小时)
乙或丙的行程,就等于全程,以乙为例,列方程如下:
36x+x+4x=36
x=36
x=
所以最短用时:
x+x+x=x=×=(小时)
答:三人同时到达的最短时间为小时.
点评:此题较复杂,应抓住甲乙丙三人行驶的时间、路程以及他们各自间的距离关系这个关键,进而分析解答即可.
32.44千米
【详解】试题分析:设AB两城相距s千米,从开始到到达C站所用时间为t,到达C站时,甲走的路程为(1.5s+6)千米,乙走的路程为(1.5s﹣6)千米,根据甲、乙两辆汽车的速度比是6:5,列式解答即可.
解:设AB两城相距s千米,从开始到到达C站所用时间为t,
5(1.5s+6)=6(1.5s﹣6)
7.5s+30=9s﹣36
30+36=9s﹣7.5s
66=1.5s
s=44,
答:AB两城相距44千米.
点评:本题考查了简单的行程问题以及比的应用.关键是得出到达C站时,甲走的路程为(1.5s+6)千米,乙走的路程为(1.5s﹣6)千米.
33.6π米
【分析】要求第三条跑道应该画在第一条跑道线前面多少米时,直线跑道的长度不变,可以不考虑,只需要考虑直径第三条跑道比第一条跑道之间环宽差,用它们之间的环宽差乘2再乘圆周率即可。
【详解】1.5×2×3=9(米)
1.5×2=3(米)
(9-3)π=6π(米)
答:第三条跑道线应该画在第一条跑道线前面6π米处。
【点睛】本题考查了圆的周长,圆的周长=2πr。
答案第1页,共2页
答案第1页,共2页
同课章节目录
