人教版六年级上册 方圆之间的面积关系 教学设计(表格式)
文档属性
| 名称 | 人教版六年级上册 方圆之间的面积关系 教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-19 00:00:00 | ||
图片预览


文档简介
方圆之间的面积关系(六上p69-70例3)
教材分析 本节课是教材新增加的内容,安排在学习了圆面积计算公式之后,通过让学生解决圆与其内切和外切正方形之间的面积这一实际问题,经历解决问题的全过程,并在解决问题的基础上发现更为一般的数学规律。提高学生发现问题、提出问题、分析问题、解决问题的能力。教学重点:圆与正方形之间的面积关系的理解。教学难点:发现问题、提出问题、分析问题、解决问题的能力的培养。
教学目标 学生经历猜想—验证的过程,自主探究外方内圆和外圆内方图形中正方形和圆之间的面积与半径的关系,并能运用关系解决实际问题。在问题解决的过程中,使学生进一步体会用“假设法”的策略解决问题的思路,感受解决问题策略的实际应用价值。在新知探究的过程中,培养学生小组合作的意识,激发学生的学习兴趣。让学生感受“方与圆”的美,体会数学文化的魅力。
教学过程设计建议 个性化设计
环节 层次 环节目标导向 问题设计导引 主体设计(活动,组织,问题,练习编排) 调整意图
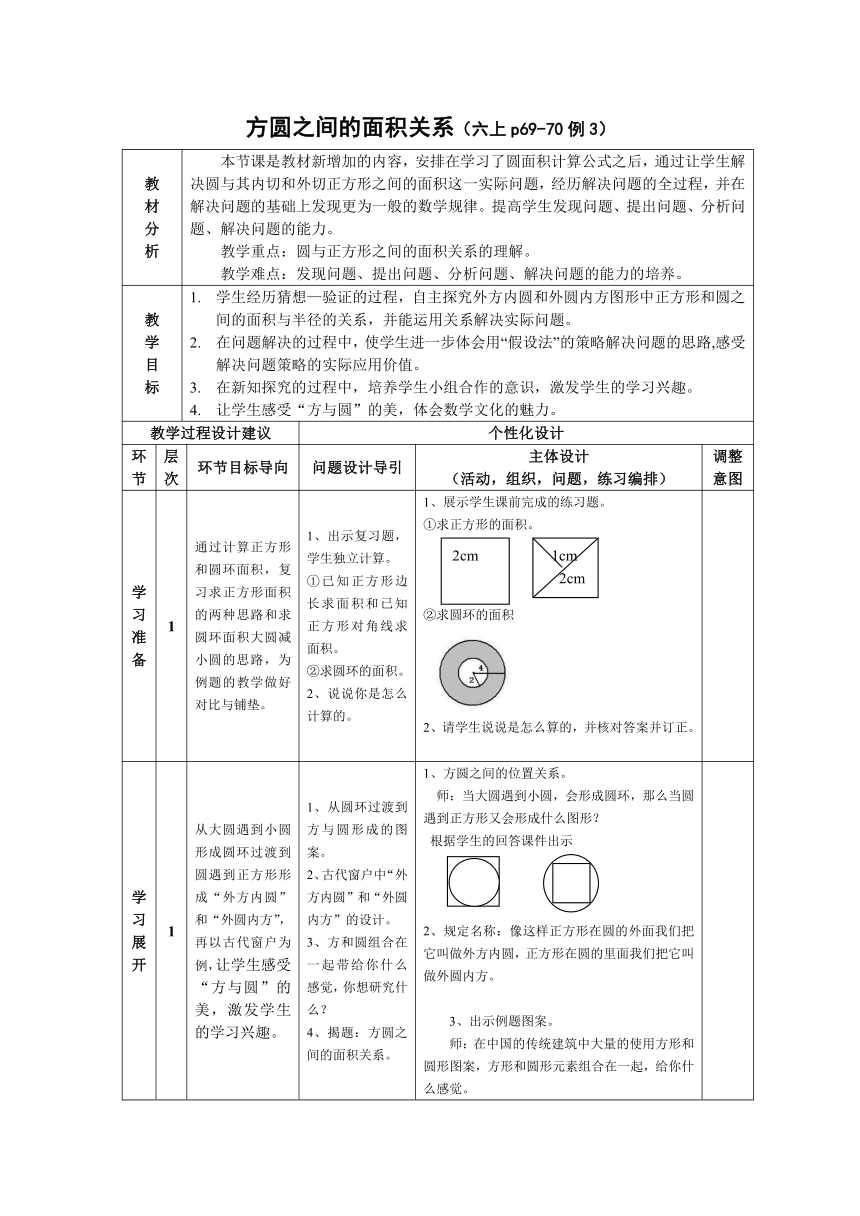
学习准备 1 通过计算正方形和圆环面积,复习求正方形面积的两种思路和求圆环面积大圆减小圆的思路,为例题的教学做好对比与铺垫。 1、出示复习题,学生独立计算。①已知正方形边长求面积和已知正方形对角线求面积。②求圆环的面积。2、说说你是怎么计算的。 1、展示学生课前完成的练习题。①求正方形的面积。②求圆环的面积2、请学生说说是怎么算的,并核对答案并订正。
学习展开 1 从大圆遇到小圆形成圆环过渡到圆遇到正方形形成“外方内圆”和“外圆内方”,再以古代窗户为例,让学生感受“方与圆”的美,激发学生的学习兴趣。 1、从圆环过渡到方与圆形成的图案。2、古代窗户中“外方内圆”和“外圆内方”的设计。3、方和圆组合在一起带给你什么感觉,你想研究什么?4、揭题:方圆之间的面积关系。 1、方圆之间的位置关系。 师:当大圆遇到小圆,会形成圆环,那么当圆遇到正方形又会形成什么图形? 根据学生的回答课件出示2、规定名称:像这样正方形在圆的外面我们把它叫做外方内圆,正方形在圆的里面我们把它叫做外圆内方。3、出示例题图案。师:在中国的传统建筑中大量的使用方形和圆形图案,方形和圆形元素组合在一起,给你什么感觉。师:是啊,方和圆组合在一起使建筑更加具有中国味。那么这样的设计又能带给我们什么数学知识呢? 揭题:方圆之间的面积关系。
2 通过假设圆的半径为1厘米,让学生学会求圆与外切正方形之间的面积。 出示例题,让学生说说获取了哪些数学信息。抽生说说求外方内圆图案中方圆之间面积的方法。学生独立计算(圆半径等于1厘米)。展示学生答案并交流方法。 1、媒体出示:这是中国建筑中常见的“外方内圆”的设计,你能求出正方形和圆之间部分的面积吗?它的面积与谁有关?有什么样的关系? 2、请学生阅读上述文字,说说获取了什么信息? 3、师:你觉得方圆之间的面积会与谁有关?如何验证你的猜想。 师:要想求出方圆之间的面积,条件不够怎么办?(引导学生用假设法来解决这个问题) 4、假设圆的半径是1米,探究“外方内圆”图形中,正方形与圆之间部分的面积。 ①请学生在练习纸中完成半径等于1时的填空。 ②抽生说说你是怎么在计算的,媒体展示计算过程,全班核对答案并订正。
3 通过假设其它圆的半径,让学生顺势发现圆与外切正方形的关系。 学生独立计算半径等于其他数据时圆与外切正方形的面积。组内交流方圆之间的面积与谁有关。师生共同对比,发现圆与外切正方形之间的关系。 1、假设圆的半径等于其他数据时,(引导学生假设时要选择简单又具有代表性的数字,如2,10)求出“正方形与圆之间部分的面积。 2、学生独立计算。 3、组内交流方圆之间的面积与谁有关。 4、师抽生汇报数据,全班比对,初步体会圆与外切正方形的关系。 ①师根据学生汇报板书0.86×1 、0.86×2 、0.86×10 . ②通过比对,顺势发现圆与外切正方形的面积与圆的半径有关,它的面积是半径平方的0.86倍。
4 通过假设圆的半径等于r,论证发现的规律,让结论更具科学性。 计算半径等于r时圆与外切正方形的面积。小结圆与外切正方形之间的关系。 引导学生假设圆的半径等于r时,“外方内圆”图形中,正方形与圆之间部分的面积。教师板书计算过程: 正方形的面积=2r×2r=4r 圆的面积=3.14 r 方圆之间的面积=4r -3.14 r =0.86r 2、小结:通过刚才的验证,你们发现了什么? 外方内圆图形中正方形与圆之间的面积都可以用0.86 r 来表示。
5 利用刚才的学习经验,组内共同探究圆与内接正方形之间的关系。 以小组为单位每人假设一个数据计算圆与内接正方形的面积。组内把数据合在一起,比对、探讨圆与内接正方形之间面积与半径的关系。小结,得出结论。 媒体出示学习任务,这是中国建筑中常见的“外圆内方”的设计。 请你根据表格假设一个数据计算方圆之间的面积。 4人小组讨论外圆内方的面积与什么有关,有着怎样的关系。2、以4人小组为单位,共同完成下表:半径 = 半径 = 半径 = 半径 = r圆面积正方形面积s圆-s正方形我发现了: 3、由组长负责,各组员分工合作。要求既快又合理地完成表格的填写,完成后各组选代表上台回报。4、小结:通过刚才的学习,你们又有哪些收获?外圆内方图形中,正方形与圆之间的面积与圆的半径有关,是圆半径平方的1.14倍,可以用1.14r 来表示。
6 回顾梳理学法 回顾学法:猜想—假设—计算—比对—验证 今天我们是怎样展开今天的内容的?生反馈,教师小结形成板书:猜想—假设—计算—比对—验证
巩固练习 1 模仿练习 教材70页做一做。 学生独立完成并反馈两种做法,比较两种算法的优劣。
2 开放题,拓展学生的视野 圆还与什么图形有着怎样的关系? 师:圆环的面积与圆的半径有关,方圆之间的面积也与圆的半径有关,那么圆还与什么图形有关呢 也是否与圆的半径有关呢?课后大家也可以用今天学习的方法去去研究一下。
总结 回顾学习内容 今天这节课有什么收获?
实践反思 板书设计
方圆之间的面积关系 (猜想—假设—计算—比对—验证) 外方内圆:正方形面积—圆面积 圆的半径: 1 2 10 …… r方圆之间的面积:0.86×1 0.86×2 0.86×10 …… 0.86×r 外圆内方:圆面积— 正方形面积 圆的半径: 1 2 10 …… r方圆之间的面积:1.14×1 1.14×2 1.14×10 …… 1.14×r
2cm
1cm
2cm
教材分析 本节课是教材新增加的内容,安排在学习了圆面积计算公式之后,通过让学生解决圆与其内切和外切正方形之间的面积这一实际问题,经历解决问题的全过程,并在解决问题的基础上发现更为一般的数学规律。提高学生发现问题、提出问题、分析问题、解决问题的能力。教学重点:圆与正方形之间的面积关系的理解。教学难点:发现问题、提出问题、分析问题、解决问题的能力的培养。
教学目标 学生经历猜想—验证的过程,自主探究外方内圆和外圆内方图形中正方形和圆之间的面积与半径的关系,并能运用关系解决实际问题。在问题解决的过程中,使学生进一步体会用“假设法”的策略解决问题的思路,感受解决问题策略的实际应用价值。在新知探究的过程中,培养学生小组合作的意识,激发学生的学习兴趣。让学生感受“方与圆”的美,体会数学文化的魅力。
教学过程设计建议 个性化设计
环节 层次 环节目标导向 问题设计导引 主体设计(活动,组织,问题,练习编排) 调整意图
学习准备 1 通过计算正方形和圆环面积,复习求正方形面积的两种思路和求圆环面积大圆减小圆的思路,为例题的教学做好对比与铺垫。 1、出示复习题,学生独立计算。①已知正方形边长求面积和已知正方形对角线求面积。②求圆环的面积。2、说说你是怎么计算的。 1、展示学生课前完成的练习题。①求正方形的面积。②求圆环的面积2、请学生说说是怎么算的,并核对答案并订正。
学习展开 1 从大圆遇到小圆形成圆环过渡到圆遇到正方形形成“外方内圆”和“外圆内方”,再以古代窗户为例,让学生感受“方与圆”的美,激发学生的学习兴趣。 1、从圆环过渡到方与圆形成的图案。2、古代窗户中“外方内圆”和“外圆内方”的设计。3、方和圆组合在一起带给你什么感觉,你想研究什么?4、揭题:方圆之间的面积关系。 1、方圆之间的位置关系。 师:当大圆遇到小圆,会形成圆环,那么当圆遇到正方形又会形成什么图形? 根据学生的回答课件出示2、规定名称:像这样正方形在圆的外面我们把它叫做外方内圆,正方形在圆的里面我们把它叫做外圆内方。3、出示例题图案。师:在中国的传统建筑中大量的使用方形和圆形图案,方形和圆形元素组合在一起,给你什么感觉。师:是啊,方和圆组合在一起使建筑更加具有中国味。那么这样的设计又能带给我们什么数学知识呢? 揭题:方圆之间的面积关系。
2 通过假设圆的半径为1厘米,让学生学会求圆与外切正方形之间的面积。 出示例题,让学生说说获取了哪些数学信息。抽生说说求外方内圆图案中方圆之间面积的方法。学生独立计算(圆半径等于1厘米)。展示学生答案并交流方法。 1、媒体出示:这是中国建筑中常见的“外方内圆”的设计,你能求出正方形和圆之间部分的面积吗?它的面积与谁有关?有什么样的关系? 2、请学生阅读上述文字,说说获取了什么信息? 3、师:你觉得方圆之间的面积会与谁有关?如何验证你的猜想。 师:要想求出方圆之间的面积,条件不够怎么办?(引导学生用假设法来解决这个问题) 4、假设圆的半径是1米,探究“外方内圆”图形中,正方形与圆之间部分的面积。 ①请学生在练习纸中完成半径等于1时的填空。 ②抽生说说你是怎么在计算的,媒体展示计算过程,全班核对答案并订正。
3 通过假设其它圆的半径,让学生顺势发现圆与外切正方形的关系。 学生独立计算半径等于其他数据时圆与外切正方形的面积。组内交流方圆之间的面积与谁有关。师生共同对比,发现圆与外切正方形之间的关系。 1、假设圆的半径等于其他数据时,(引导学生假设时要选择简单又具有代表性的数字,如2,10)求出“正方形与圆之间部分的面积。 2、学生独立计算。 3、组内交流方圆之间的面积与谁有关。 4、师抽生汇报数据,全班比对,初步体会圆与外切正方形的关系。 ①师根据学生汇报板书0.86×1 、0.86×2 、0.86×10 . ②通过比对,顺势发现圆与外切正方形的面积与圆的半径有关,它的面积是半径平方的0.86倍。
4 通过假设圆的半径等于r,论证发现的规律,让结论更具科学性。 计算半径等于r时圆与外切正方形的面积。小结圆与外切正方形之间的关系。 引导学生假设圆的半径等于r时,“外方内圆”图形中,正方形与圆之间部分的面积。教师板书计算过程: 正方形的面积=2r×2r=4r 圆的面积=3.14 r 方圆之间的面积=4r -3.14 r =0.86r 2、小结:通过刚才的验证,你们发现了什么? 外方内圆图形中正方形与圆之间的面积都可以用0.86 r 来表示。
5 利用刚才的学习经验,组内共同探究圆与内接正方形之间的关系。 以小组为单位每人假设一个数据计算圆与内接正方形的面积。组内把数据合在一起,比对、探讨圆与内接正方形之间面积与半径的关系。小结,得出结论。 媒体出示学习任务,这是中国建筑中常见的“外圆内方”的设计。 请你根据表格假设一个数据计算方圆之间的面积。 4人小组讨论外圆内方的面积与什么有关,有着怎样的关系。2、以4人小组为单位,共同完成下表:半径 = 半径 = 半径 = 半径 = r圆面积正方形面积s圆-s正方形我发现了: 3、由组长负责,各组员分工合作。要求既快又合理地完成表格的填写,完成后各组选代表上台回报。4、小结:通过刚才的学习,你们又有哪些收获?外圆内方图形中,正方形与圆之间的面积与圆的半径有关,是圆半径平方的1.14倍,可以用1.14r 来表示。
6 回顾梳理学法 回顾学法:猜想—假设—计算—比对—验证 今天我们是怎样展开今天的内容的?生反馈,教师小结形成板书:猜想—假设—计算—比对—验证
巩固练习 1 模仿练习 教材70页做一做。 学生独立完成并反馈两种做法,比较两种算法的优劣。
2 开放题,拓展学生的视野 圆还与什么图形有着怎样的关系? 师:圆环的面积与圆的半径有关,方圆之间的面积也与圆的半径有关,那么圆还与什么图形有关呢 也是否与圆的半径有关呢?课后大家也可以用今天学习的方法去去研究一下。
总结 回顾学习内容 今天这节课有什么收获?
实践反思 板书设计
方圆之间的面积关系 (猜想—假设—计算—比对—验证) 外方内圆:正方形面积—圆面积 圆的半径: 1 2 10 …… r方圆之间的面积:0.86×1 0.86×2 0.86×10 …… 0.86×r 外圆内方:圆面积— 正方形面积 圆的半径: 1 2 10 …… r方圆之间的面积:1.14×1 1.14×2 1.14×10 …… 1.14×r
2cm
1cm
2cm
