人教版 八年级上册 11.2.1三角形内角 说课课件(共22张PPT)
文档属性
| 名称 | 人教版 八年级上册 11.2.1三角形内角 说课课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
《说课课件》
11.2.1《三角形的内角》
CONTENTS
目 录
1
教材分析
4
教学学法
2
学情分析
3
教学目标与教学重难点
6
板书设计
5
教学过程
01 教材分析
请在此处添加标题文字
地位和作用
本章是学生学习了直线、射线、线段、相交线与平行线等知识后,第一次全面深入地研究平面图形。学生在学习了与三角形有关的线段和角的基础上,再学习多边形的有关知识,这样的编排符合学生由简单到复杂的认知规律。另外,本章借助之前所学的线段、角、平面图形等知识,为今后学习“全等三角形”“轴对称”等其他内容打下基础。基于以上分析,将本节课的教学重点确定为:探究三角形内角和定理。
02 学情分析
请在此处添加标题文字
本节课的教学对象是八年级学生,他们对几何的感知以具体形象的图形为主,逐渐具备抽象逻辑的能力,开始由经验型向理论型转化,有一定观察、记忆、想象的能力。本节课设计了学生亲身实践探究的一系列活动,并在活动中配以学生活动的教具。为了准确了解学生的已有知识要素或技能的认知水平,在课前对40名学生做了如下前测。
在进行“与三角形有关的角”这一内容的教学之前,为了了解学生的认知基础,对任教班级40名学生开展了问卷调查。调查题目是:
问题1和问题2均被回答正确。对于问题3,学生的作答情况如表所示:
问题 1.在△ABC中,∠A=30°,∠B=40°,则∠C=
问题 2.解决问题1的依据是什么
问题 3.你觉得这个依据一定正确吗 为什么
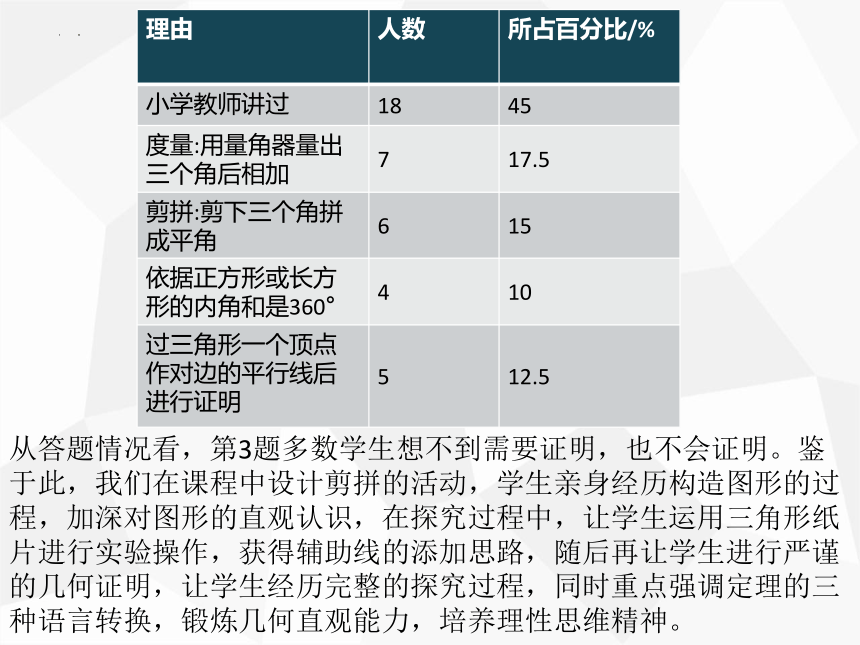
理由 人数 所占百分比/%
小学教师讲过 18 45
度量:用量角器量出三个角后相加 7 17.5
剪拼:剪下三个角拼成平角 6 15
依据正方形或长方形的内角和是360° 4 10
过三角形一个顶点作对边的平行线后进行证明 5 12.5
从答题情况看,第3题多数学生想不到需要证明,也不会证明。鉴于此,我们在课程中设计剪拼的活动,学生亲身经历构造图形的过程,加深对图形的直观认识,在探究过程中,让学生运用三角形纸片进行实验操作,获得辅助线的添加思路,随后再让学生进行严谨的几何证明,让学生经历完整的探究过程,同时重点强调定理的三种语言转换,锻炼几何直观能力,培养理性思维精神。
03 教学目标
请在此处添加标题文字
1)知识与技能目标:掌握“三角形内角和定理”的证明及其简单应用
2)过程与方法目标:经历探索三角形内角和的研究过程,能应用所学知识解决简单的问题,训练学生对所学知识的应用能力。
3)情感太度价值观:通过学生积极参与数学活动,培养学生对数学的好奇心及求知欲。由具体实例的引导,让学生初步认识数学与人类生活的密切联系。
03 教学重难点
教学重点:探究并证明三角形内角和定理。
教学难点:三角形内角和定理的证明时辅助线的添加。
04 教法学法
说教法
根据课程的特点,本节课以创设问题情境 ,引导学生探索、运用为主线来展开。采用了教具演示的教学手段,使图形直观、形象地便于学生理解。以学生发展为本的原则,我运用启发式教学方法,引导学生动手操作、探索、讨论、归纳。在教学过程中,引导学生去探索,使学生感受到添加辅助线的数学思想,更好地掌握三角形内角和定理的证明及简单的应用,从而实现教师是引导者和学生是主体者的课堂教学理念。
04 教法学法
说学法
根据本节课特点和学生的实际,八年级学生基本具备动手操作、探索讨论、猜想、说理的能力,主要采用“操作—观察—讨论—证明—应用 ”的探究式的学习方式,教会学生“ 动手做,动脑想,大胆猜、会说,学致用”的学习方法。增加学生参与的机会,使学生在掌握知识、形成技能的同时,培养科学的学习方法和自信心。
05 教学过程
请在此处添加标题文字
(一)激发兴趣,体验方法
(二)动手操作,探索新知
(三)探索新知,合作交流
(四)应用新知,解决问题
(五)设疑激趣,课堂小结
(一)激发兴趣,体验方法
一天,三角形界就三角形内角和的大小展开了一场激烈的争论,请同学们为它们评判一下吧.
我是直角三角形,我的内角和最大
我有一个钝角,比你的三个角都大,所以我的内角和才是最大的
我虽然是锐角三角形,但是我的个头最大,所以我的内角和才是最大的
(二)动手操作,探索新知
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
三角形的三个内角拼到一起恰好构成一个平角.
还有其他的拼接方法吗?
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
(三)探索新知,合作交流
通过度量或简拼的方法,可以验证三角形的内角和等于180度.但是由于测量常常有误差,这种“验证”不是数学“证明”,不能完全让人信服;又由于形状不同的三角形有无数个,我们不可能用上述方法一一验证所有三角形的内角和等于180°.所以需要通过推理的方法去证明:任意一个三角形的内角和等于180°。
验证结论:
三角形三个内角的和等于180°.
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
1
2
D
E
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
C
B
A
E
D
F
A
B
C
D
E
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
借助平行线的“移角”的功能,将三个角转化成一个平角.
思考:多种方法证明三角形内角和等于180°的核心是什么?
(四)应用新知,解决问题
基础练习
要求学生利用“三角形内角和是180°”在三角形内已知两个角,求第三个角。
提高练习
爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
扩展练习
要求学生推导三角形的外角等于与它不相邻的两个内角的和。
(五)设疑激趣,课堂小结
还有没有其他证明方法,也可以证明角形的内角和是180°?
总结归纳
★作辅助线
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
★思路总结
为了证明三角形三个内角的和为180°,常将三个角转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
06 说板书设计与教学反思
三角形内角和定理
已知:------------
求证:------------
证明:------------
例题讲解:
证明:-----------------
------------------------
------------------------
------------------------
------------------------
习题讲解:
---------------------
--------------------
--------------------
感谢聆听!
《说课课件》
11.2.1《三角形的内角》
CONTENTS
目 录
1
教材分析
4
教学学法
2
学情分析
3
教学目标与教学重难点
6
板书设计
5
教学过程
01 教材分析
请在此处添加标题文字
地位和作用
本章是学生学习了直线、射线、线段、相交线与平行线等知识后,第一次全面深入地研究平面图形。学生在学习了与三角形有关的线段和角的基础上,再学习多边形的有关知识,这样的编排符合学生由简单到复杂的认知规律。另外,本章借助之前所学的线段、角、平面图形等知识,为今后学习“全等三角形”“轴对称”等其他内容打下基础。基于以上分析,将本节课的教学重点确定为:探究三角形内角和定理。
02 学情分析
请在此处添加标题文字
本节课的教学对象是八年级学生,他们对几何的感知以具体形象的图形为主,逐渐具备抽象逻辑的能力,开始由经验型向理论型转化,有一定观察、记忆、想象的能力。本节课设计了学生亲身实践探究的一系列活动,并在活动中配以学生活动的教具。为了准确了解学生的已有知识要素或技能的认知水平,在课前对40名学生做了如下前测。
在进行“与三角形有关的角”这一内容的教学之前,为了了解学生的认知基础,对任教班级40名学生开展了问卷调查。调查题目是:
问题1和问题2均被回答正确。对于问题3,学生的作答情况如表所示:
问题 1.在△ABC中,∠A=30°,∠B=40°,则∠C=
问题 2.解决问题1的依据是什么
问题 3.你觉得这个依据一定正确吗 为什么
理由 人数 所占百分比/%
小学教师讲过 18 45
度量:用量角器量出三个角后相加 7 17.5
剪拼:剪下三个角拼成平角 6 15
依据正方形或长方形的内角和是360° 4 10
过三角形一个顶点作对边的平行线后进行证明 5 12.5
从答题情况看,第3题多数学生想不到需要证明,也不会证明。鉴于此,我们在课程中设计剪拼的活动,学生亲身经历构造图形的过程,加深对图形的直观认识,在探究过程中,让学生运用三角形纸片进行实验操作,获得辅助线的添加思路,随后再让学生进行严谨的几何证明,让学生经历完整的探究过程,同时重点强调定理的三种语言转换,锻炼几何直观能力,培养理性思维精神。
03 教学目标
请在此处添加标题文字
1)知识与技能目标:掌握“三角形内角和定理”的证明及其简单应用
2)过程与方法目标:经历探索三角形内角和的研究过程,能应用所学知识解决简单的问题,训练学生对所学知识的应用能力。
3)情感太度价值观:通过学生积极参与数学活动,培养学生对数学的好奇心及求知欲。由具体实例的引导,让学生初步认识数学与人类生活的密切联系。
03 教学重难点
教学重点:探究并证明三角形内角和定理。
教学难点:三角形内角和定理的证明时辅助线的添加。
04 教法学法
说教法
根据课程的特点,本节课以创设问题情境 ,引导学生探索、运用为主线来展开。采用了教具演示的教学手段,使图形直观、形象地便于学生理解。以学生发展为本的原则,我运用启发式教学方法,引导学生动手操作、探索、讨论、归纳。在教学过程中,引导学生去探索,使学生感受到添加辅助线的数学思想,更好地掌握三角形内角和定理的证明及简单的应用,从而实现教师是引导者和学生是主体者的课堂教学理念。
04 教法学法
说学法
根据本节课特点和学生的实际,八年级学生基本具备动手操作、探索讨论、猜想、说理的能力,主要采用“操作—观察—讨论—证明—应用 ”的探究式的学习方式,教会学生“ 动手做,动脑想,大胆猜、会说,学致用”的学习方法。增加学生参与的机会,使学生在掌握知识、形成技能的同时,培养科学的学习方法和自信心。
05 教学过程
请在此处添加标题文字
(一)激发兴趣,体验方法
(二)动手操作,探索新知
(三)探索新知,合作交流
(四)应用新知,解决问题
(五)设疑激趣,课堂小结
(一)激发兴趣,体验方法
一天,三角形界就三角形内角和的大小展开了一场激烈的争论,请同学们为它们评判一下吧.
我是直角三角形,我的内角和最大
我有一个钝角,比你的三个角都大,所以我的内角和才是最大的
我虽然是锐角三角形,但是我的个头最大,所以我的内角和才是最大的
(二)动手操作,探索新知
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
三角形的三个内角拼到一起恰好构成一个平角.
还有其他的拼接方法吗?
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
(三)探索新知,合作交流
通过度量或简拼的方法,可以验证三角形的内角和等于180度.但是由于测量常常有误差,这种“验证”不是数学“证明”,不能完全让人信服;又由于形状不同的三角形有无数个,我们不可能用上述方法一一验证所有三角形的内角和等于180°.所以需要通过推理的方法去证明:任意一个三角形的内角和等于180°。
验证结论:
三角形三个内角的和等于180°.
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
1
2
D
E
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
C
B
A
E
D
F
A
B
C
D
E
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
借助平行线的“移角”的功能,将三个角转化成一个平角.
思考:多种方法证明三角形内角和等于180°的核心是什么?
(四)应用新知,解决问题
基础练习
要求学生利用“三角形内角和是180°”在三角形内已知两个角,求第三个角。
提高练习
爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
扩展练习
要求学生推导三角形的外角等于与它不相邻的两个内角的和。
(五)设疑激趣,课堂小结
还有没有其他证明方法,也可以证明角形的内角和是180°?
总结归纳
★作辅助线
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
★思路总结
为了证明三角形三个内角的和为180°,常将三个角转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
06 说板书设计与教学反思
三角形内角和定理
已知:------------
求证:------------
证明:------------
例题讲解:
证明:-----------------
------------------------
------------------------
------------------------
------------------------
习题讲解:
---------------------
--------------------
--------------------
感谢聆听!
