1.1 相似多边形 课件(共24张PPT)
文档属性
| 名称 | 1.1 相似多边形 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 853.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-21 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
(青岛版)9年级
上
1.1 相似多边形
第1章
“—”
一、什么叫做全等形?
能够完全重合的两个平面图形叫全等形。
二、怎样理解“完全重合”?
完全重合:即形状相同、大小相等。
在全等多边形中重点学习的全等三角形
三、三角形全等的判定方法:
(1)ASA;(2)AAS;(3)SAS;(4)SSS。
四、三角形全等的性质:
1、全等三角形的对应角相等;
2、全等三角形的对应边相等。
学习目标
图中的五颗五角星的形状相同吗?大小相等吗?
思考:现实生活中,你还见过形状相同但大小未必相等的图形吗?
新知导入
探究一:全等形与相似形有什么关系?
大小相等,形状相同的平面图形叫做全等形.
形状相同的平面图形叫做相似形.
两个全等形也是相似形;
两个相似形未必是全等形.
全等形是特殊的相似形
相似
全等
新知探究
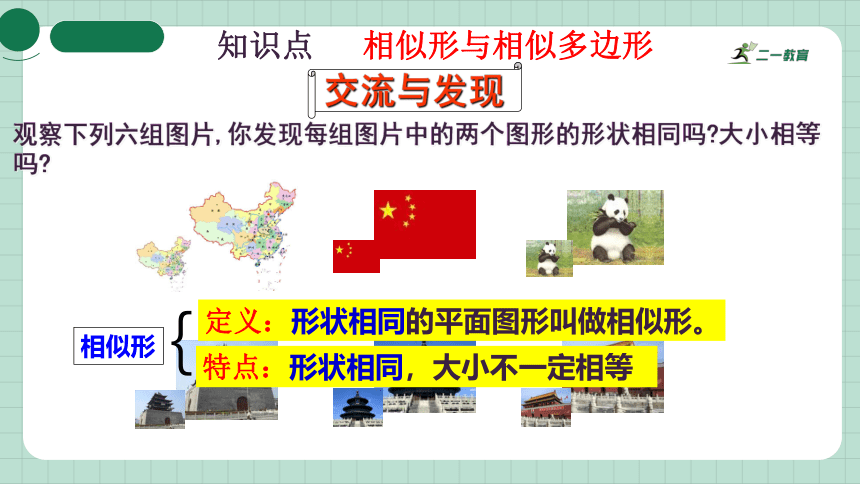
知识点 相似形与相似多边形
观察下列六组图片,你发现每组图片中的两个图形的形状相同吗 大小相等吗
交流与发现
定义:形状相同的平面图形叫做相似形。
相似形
{
特点:形状相同,大小不一定相等
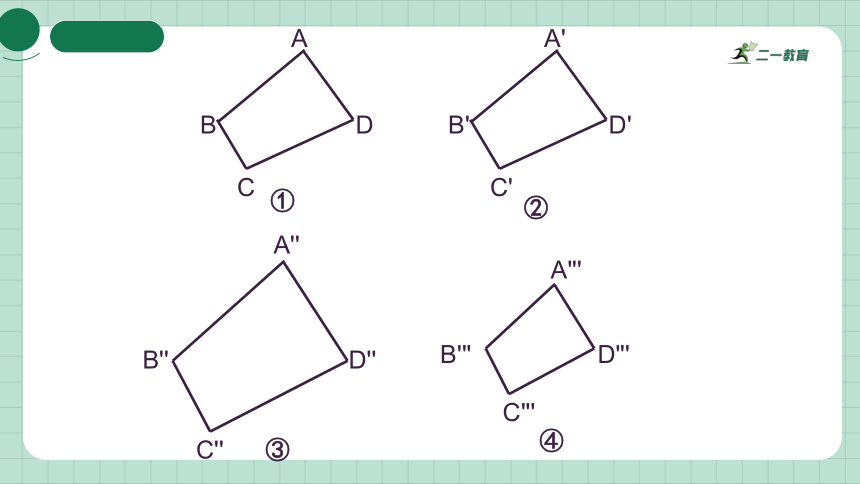
A
B
C
D
A'
B'
C'
D'
①
A''
B''
C''
D''
②
③
A'''
B'''
C'''
D'''
④
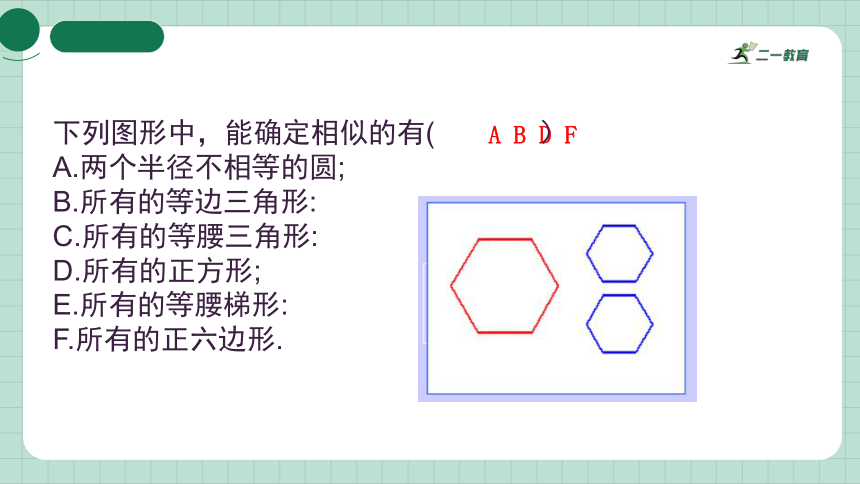
A B D F
下列图形中,能确定相似的有( )
A.两个半径不相等的圆;
B.所有的等边三角形:
C.所有的等腰三角形:
D.所有的正方形;
E.所有的等腰梯形:
F.所有的正六边形.
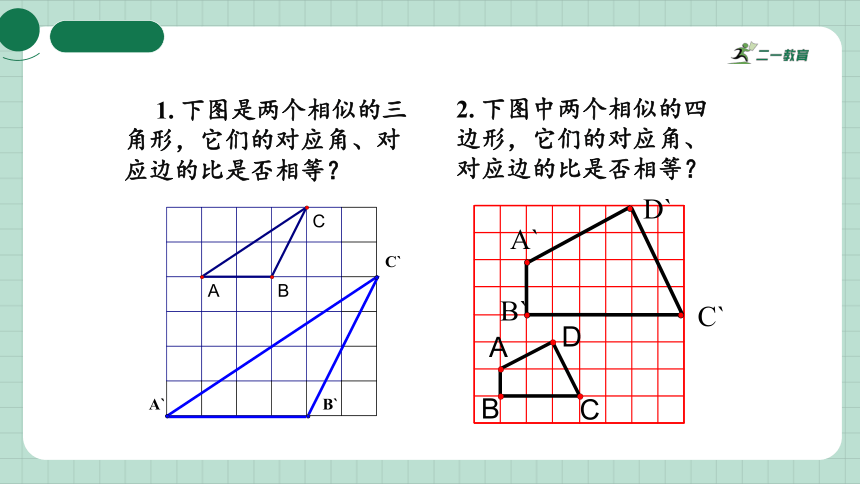
1. 下图是两个相似的三角形,它们的对应角、对应边的比是否相等?
2. 下图中两个相似的四边形,它们的对应角、对应边的比是否相等?
A`
B`
C`
C`
B`
A`
D`
将四边形ABCD各角的大小保持不变,将它的各边同时缩小 ,得到四边形A′B′C′D′,
各角对应相等,
各边对应成比例.
两个四边形相似
(1)它们的形状相同吗?是相似形吗?
(2)它们的各角与各边存在怎样的数量关系?
(3)用数学符号表示出来。
符号语言:
∵四边形ABCD∽四边形A′B′C′D′
∴四边形ABCD∽四边形A′B′C′D′
性质
判定
性质
判定
知识点 相似多边形的性质
相似比:
相似多边形的特征:
相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形.
相似多边形的对应角相等,对应边成比例.
相似多边形的对应边的比叫作相似比.
注 意
(2)符号“∽”读作“相似于”
(3)对应顶点的字母写在对应的位置上
注意:①相似比是有顺序的.
②当两个多边形的相似比为1:1时,这两个多边形 .
全等
≌
形状相同
大小相等
(1)四边形ABCD与四边形A’B’C’D’相似,记作:四边形ABCD∽四边形A’B’C’D’
如图,已知四边形AEFD~四边形EBCF.
(1) 写出它们相等的角及对应边的比例式;
(2) 若AD=3,EF=4,求 BC的长.
(1)在四边形AEFD 和四边形 EBCF 中,
∵四边形AEFD ~四边形EBCF,
∴ ∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC. 并且 = = = .
(2)∵AD=3,EF=4. 代入 = 得:
= .
解得:BC =.
由两个多边形的各个角分别相等,能断定它们相似吗 由两个多边形的边对应成比例,能断定它们相似吗 如果不能,请分别举出反例;如果能,说明你的理由.
两多边形相似的判定方法:
若两多边形边数相同;各角对应相等;各边对应成比例,那么这两多边形相似
相似多边形的性质:
相似多边形的对应角相等;相似多边形的对应边成比例。
1、(多选题)下列说法正确的是( )
A.放大(缩小)的图片与原图片是相似图形;
B.比例尺不同的中国地图是相似图形;
C.放大镜下的五角星与原来的五角星是相似图形;
D.放电影时胶片上的图形和它映射到屏幕上的画面是相似图形.
ABCD
课堂练习
2、如图,用放大镜看到的多边形与原多边形相比较,不发生改变的是( )
A.周长 B.面积 C.每个内角的度数 D.每条边的长度
C
解:∵四边形ABCD∽四边形EFGH,
∴∠α=∠C=83°,∠A=∠E=118°,
在四边形EFGH中,∠β=360°-83°-78°-118°=81°,
∵四边形ABCD∽四边形EFGH,
∴EH:AD=EF:AB,
∴x:21=24:18,
解得x=28,
3、如图,四边形ABCD∽四边形EFGH,求∠α、∠β 的大小和EH的长度.
1. 相似多边形的概念
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等、各边对应成比例那么这两个多边形叫做相似多边形.
课堂总结
2. 相似比的概念
相似多边形对应边的比叫做相似比。
3. 两个多边形相似的表示方法
∽
相似多边形的对应角相等,
对应边成比例.
4、 相似多边形的性质
1. 课本练习1,2
2.习题1.1
3.预习1.2.1平行线分线段成比例
作业布置
23
Thanks!
2
https://www.21cnjy.com/help/help_extract.php
(青岛版)9年级
上
1.1 相似多边形
第1章
“—”
一、什么叫做全等形?
能够完全重合的两个平面图形叫全等形。
二、怎样理解“完全重合”?
完全重合:即形状相同、大小相等。
在全等多边形中重点学习的全等三角形
三、三角形全等的判定方法:
(1)ASA;(2)AAS;(3)SAS;(4)SSS。
四、三角形全等的性质:
1、全等三角形的对应角相等;
2、全等三角形的对应边相等。
学习目标
图中的五颗五角星的形状相同吗?大小相等吗?
思考:现实生活中,你还见过形状相同但大小未必相等的图形吗?
新知导入
探究一:全等形与相似形有什么关系?
大小相等,形状相同的平面图形叫做全等形.
形状相同的平面图形叫做相似形.
两个全等形也是相似形;
两个相似形未必是全等形.
全等形是特殊的相似形
相似
全等
新知探究
知识点 相似形与相似多边形
观察下列六组图片,你发现每组图片中的两个图形的形状相同吗 大小相等吗
交流与发现
定义:形状相同的平面图形叫做相似形。
相似形
{
特点:形状相同,大小不一定相等
A
B
C
D
A'
B'
C'
D'
①
A''
B''
C''
D''
②
③
A'''
B'''
C'''
D'''
④
A B D F
下列图形中,能确定相似的有( )
A.两个半径不相等的圆;
B.所有的等边三角形:
C.所有的等腰三角形:
D.所有的正方形;
E.所有的等腰梯形:
F.所有的正六边形.
1. 下图是两个相似的三角形,它们的对应角、对应边的比是否相等?
2. 下图中两个相似的四边形,它们的对应角、对应边的比是否相等?
A`
B`
C`
C`
B`
A`
D`
将四边形ABCD各角的大小保持不变,将它的各边同时缩小 ,得到四边形A′B′C′D′,
各角对应相等,
各边对应成比例.
两个四边形相似
(1)它们的形状相同吗?是相似形吗?
(2)它们的各角与各边存在怎样的数量关系?
(3)用数学符号表示出来。
符号语言:
∵四边形ABCD∽四边形A′B′C′D′
∴四边形ABCD∽四边形A′B′C′D′
性质
判定
性质
判定
知识点 相似多边形的性质
相似比:
相似多边形的特征:
相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形.
相似多边形的对应角相等,对应边成比例.
相似多边形的对应边的比叫作相似比.
注 意
(2)符号“∽”读作“相似于”
(3)对应顶点的字母写在对应的位置上
注意:①相似比是有顺序的.
②当两个多边形的相似比为1:1时,这两个多边形 .
全等
≌
形状相同
大小相等
(1)四边形ABCD与四边形A’B’C’D’相似,记作:四边形ABCD∽四边形A’B’C’D’
如图,已知四边形AEFD~四边形EBCF.
(1) 写出它们相等的角及对应边的比例式;
(2) 若AD=3,EF=4,求 BC的长.
(1)在四边形AEFD 和四边形 EBCF 中,
∵四边形AEFD ~四边形EBCF,
∴ ∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC. 并且 = = = .
(2)∵AD=3,EF=4. 代入 = 得:
= .
解得:BC =.
由两个多边形的各个角分别相等,能断定它们相似吗 由两个多边形的边对应成比例,能断定它们相似吗 如果不能,请分别举出反例;如果能,说明你的理由.
两多边形相似的判定方法:
若两多边形边数相同;各角对应相等;各边对应成比例,那么这两多边形相似
相似多边形的性质:
相似多边形的对应角相等;相似多边形的对应边成比例。
1、(多选题)下列说法正确的是( )
A.放大(缩小)的图片与原图片是相似图形;
B.比例尺不同的中国地图是相似图形;
C.放大镜下的五角星与原来的五角星是相似图形;
D.放电影时胶片上的图形和它映射到屏幕上的画面是相似图形.
ABCD
课堂练习
2、如图,用放大镜看到的多边形与原多边形相比较,不发生改变的是( )
A.周长 B.面积 C.每个内角的度数 D.每条边的长度
C
解:∵四边形ABCD∽四边形EFGH,
∴∠α=∠C=83°,∠A=∠E=118°,
在四边形EFGH中,∠β=360°-83°-78°-118°=81°,
∵四边形ABCD∽四边形EFGH,
∴EH:AD=EF:AB,
∴x:21=24:18,
解得x=28,
3、如图,四边形ABCD∽四边形EFGH,求∠α、∠β 的大小和EH的长度.
1. 相似多边形的概念
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等、各边对应成比例那么这两个多边形叫做相似多边形.
课堂总结
2. 相似比的概念
相似多边形对应边的比叫做相似比。
3. 两个多边形相似的表示方法
∽
相似多边形的对应角相等,
对应边成比例.
4、 相似多边形的性质
1. 课本练习1,2
2.习题1.1
3.预习1.2.1平行线分线段成比例
作业布置
23
Thanks!
2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
