1.2 怎样判定三角形相似(第1课时)课件(共23张PPT)
文档属性
| 名称 | 1.2 怎样判定三角形相似(第1课时)课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 771.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-21 06:14:57 | ||
图片预览





文档简介
(共23张PPT)
(青岛版)9年级
上
1.2怎样判定三角形相似(第1课时)
第1章
“—”
平行线的性质:
1、两直线平行,同位角相等。
2、两直线平行,内错角相等。
3、两直线平行,同旁内角互补。
当两条直线被三条平行线所截时能有什么结论呢?
复习回顾
1.通过推理掌握平行线分线段成比例定理及其推论;
2.能够利用平行线分线段成比例定理及其推论进行推理与计算.
学习目标
A
B
C
D
E
F
即对应角相等,对应边的比相等,我们说△ABC与△DEF
相似,记作 △ABC∽△DEF,△ABC和△DEF的相似比为k,
△DEF与△ABC的相似比为 .
由相似多边形的定义我们知道,在△ABC与△DEF中,
如果∠A=∠D, ∠B=∠E, ∠C=∠F,
思考:判定两个三角形相似时,是否存在简便的判定方法呢?
新知导入
学生自学课本“实验与探究”,并思考问题(1)-(5)
新知内容:
问题(1)+问题(2)
问题(3)
问题(4)+问题(5)
问题(6)
新知探究
(1)如图,直线 被平行直线 所截,交点分别
是A,B,C,D.
A
B
D
C
F
G
H
E
.
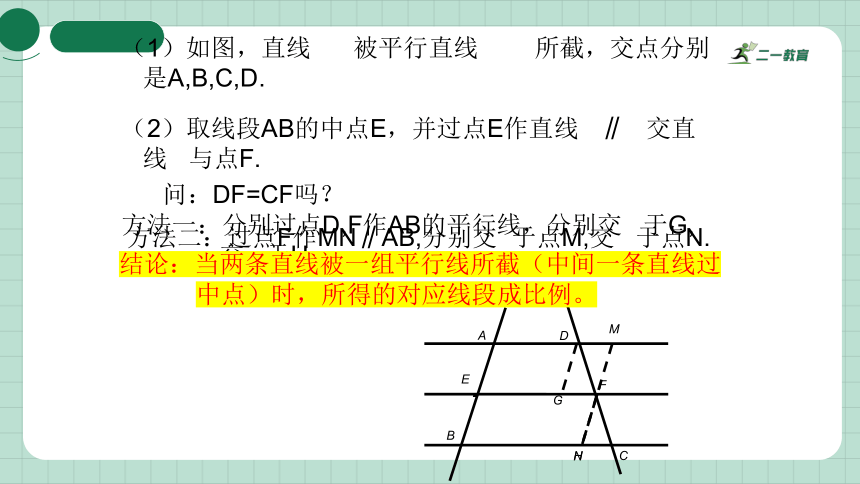
(2)取线段AB的中点E,并过点E作直线 ∥ 交直
线 与点F.
问:DF=CF吗?
N
M
方法一:分别过点D,F作AB的平行线,分别交 于G,
交 于H.
方法二:过点F作MN∥AB,分别交 于点M,交 于点N.
结论:当两条直线被一组平行线所截(中间一条直线过
中点)时,所得的对应线段成比例。
A
B
D
C
F
E
.
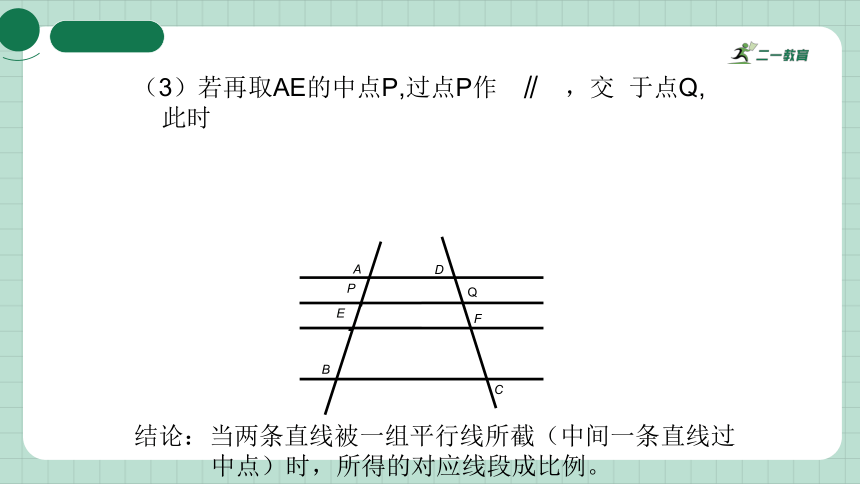
(3)若再取AE的中点P,过点P作 ∥ ,交 于点Q,
此时
P
.
Q
结论:当两条直线被一组平行线所截(中间一条直线过
中点)时,所得的对应线段成比例。
(4)一般地,如果任意两条直线l1,l2被一组平行直线l3,l4,l5所截,交点分别是A,B,C;D,E,F.你有什么结论?
结论:当两条直线被一组平行线所截(中间一条直线是
四等分点)时,所得的对应线段成比例。
A
B
D
C
F
E
.
P
.
Q
(5)如果我们这样依次再取BP或EP的中点P1,过点 P1
作 ∥ ,交 于点Q1,此时有关的比例式还成立吗?
P1
.
Q1
(6)特别地,在△ABC中,DE∥BC. ①线段AD,AB,AE, AC成比例吗?②线段AD,AB,DE,BC呢?
在本书中,把下面的命题作为第9个基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
A
B
C
D
E
l
几何语言:
若a∥b∥c,则 , …
解题技巧:寻找平行线分线的成比例定理中的对应线段,
可根据图形中的线段的对应位置确定,大致有以下几种类型:,
【问题】直线c,若直线n向左平移到B1与A1重合的位置,说说图中有哪些成比例线段?
c,∴ ,
知
识
推
广
基本图形:“A”字形
B
C
D
E
F
例1、已知:如图,在△ABC中,DE∥BC,且 DE=3,BC=12,BD=4.求:AD的长。
A
B
C
D
E
【问题】直线c,若直线n向左平移到B2与A2重合的位置,说说图中有哪些成比例线段?
c,∴ ,
基本图形:“x”字形
A
B
C
D
E
M
N
知
识
推
广
例2、已知:如图,在△ABC中,DE∥BC,且 交BA、 CA的延长线于D、E两点,DE=3,BC=12,BD=16.
求:AD的长。
A
B
C
D
E
1. 平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
2.平行于三角形一边的直线截其他两边(或两边的延长线)所得的三角形与原三角形的三边对应成比例.
A
B
C
D
E
A
B
C
D
E
A型
X型
推论
1. 如图,,若,,则( )A. B. C. D.
【详解】∵,∴.
∵,∴,
∵,,
∴,
∴.故选:D.
课堂练习
2.如图,在平行四边形ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,他们相交于G,延长BE交CD的延长线于点H,则图中的相似三角形共有 对.
4
3.如图,在△ABC中,DE∥AB,BE=2,CE=6,AD=2.5,则AC的长为________.
10
4.如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则S四边形EHFG
÷S菱形ABCD的值为
【详解】解:∵BE=2AE,DF=2FC,∴,
∵G、H分别是AC的三等分点,∴,,∴,
∴EG∥BC∴,
同理可得HF∥AD,,∴ ,
1.通过本节课的学习,你学会了哪些知识?
2. 你还记得平行线分线段成比例定理及推论的内容吗?
3.简述判定两个三角形相似的方法?
课堂总结
1.课本P17练习1,2.1
2.习题1.2 T1
3. 平行线分线段成比例定理:
4. 平行线分线段成比例定理的推论:
作业布置
22
2
https://www.21cnjy.com/help/help_extract.php
(青岛版)9年级
上
1.2怎样判定三角形相似(第1课时)
第1章
“—”
平行线的性质:
1、两直线平行,同位角相等。
2、两直线平行,内错角相等。
3、两直线平行,同旁内角互补。
当两条直线被三条平行线所截时能有什么结论呢?
复习回顾
1.通过推理掌握平行线分线段成比例定理及其推论;
2.能够利用平行线分线段成比例定理及其推论进行推理与计算.
学习目标
A
B
C
D
E
F
即对应角相等,对应边的比相等,我们说△ABC与△DEF
相似,记作 △ABC∽△DEF,△ABC和△DEF的相似比为k,
△DEF与△ABC的相似比为 .
由相似多边形的定义我们知道,在△ABC与△DEF中,
如果∠A=∠D, ∠B=∠E, ∠C=∠F,
思考:判定两个三角形相似时,是否存在简便的判定方法呢?
新知导入
学生自学课本“实验与探究”,并思考问题(1)-(5)
新知内容:
问题(1)+问题(2)
问题(3)
问题(4)+问题(5)
问题(6)
新知探究
(1)如图,直线 被平行直线 所截,交点分别
是A,B,C,D.
A
B
D
C
F
G
H
E
.
(2)取线段AB的中点E,并过点E作直线 ∥ 交直
线 与点F.
问:DF=CF吗?
N
M
方法一:分别过点D,F作AB的平行线,分别交 于G,
交 于H.
方法二:过点F作MN∥AB,分别交 于点M,交 于点N.
结论:当两条直线被一组平行线所截(中间一条直线过
中点)时,所得的对应线段成比例。
A
B
D
C
F
E
.
(3)若再取AE的中点P,过点P作 ∥ ,交 于点Q,
此时
P
.
Q
结论:当两条直线被一组平行线所截(中间一条直线过
中点)时,所得的对应线段成比例。
(4)一般地,如果任意两条直线l1,l2被一组平行直线l3,l4,l5所截,交点分别是A,B,C;D,E,F.你有什么结论?
结论:当两条直线被一组平行线所截(中间一条直线是
四等分点)时,所得的对应线段成比例。
A
B
D
C
F
E
.
P
.
Q
(5)如果我们这样依次再取BP或EP的中点P1,过点 P1
作 ∥ ,交 于点Q1,此时有关的比例式还成立吗?
P1
.
Q1
(6)特别地,在△ABC中,DE∥BC. ①线段AD,AB,AE, AC成比例吗?②线段AD,AB,DE,BC呢?
在本书中,把下面的命题作为第9个基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
A
B
C
D
E
l
几何语言:
若a∥b∥c,则 , …
解题技巧:寻找平行线分线的成比例定理中的对应线段,
可根据图形中的线段的对应位置确定,大致有以下几种类型:,
【问题】直线c,若直线n向左平移到B1与A1重合的位置,说说图中有哪些成比例线段?
c,∴ ,
知
识
推
广
基本图形:“A”字形
B
C
D
E
F
例1、已知:如图,在△ABC中,DE∥BC,且 DE=3,BC=12,BD=4.求:AD的长。
A
B
C
D
E
【问题】直线c,若直线n向左平移到B2与A2重合的位置,说说图中有哪些成比例线段?
c,∴ ,
基本图形:“x”字形
A
B
C
D
E
M
N
知
识
推
广
例2、已知:如图,在△ABC中,DE∥BC,且 交BA、 CA的延长线于D、E两点,DE=3,BC=12,BD=16.
求:AD的长。
A
B
C
D
E
1. 平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
2.平行于三角形一边的直线截其他两边(或两边的延长线)所得的三角形与原三角形的三边对应成比例.
A
B
C
D
E
A
B
C
D
E
A型
X型
推论
1. 如图,,若,,则( )A. B. C. D.
【详解】∵,∴.
∵,∴,
∵,,
∴,
∴.故选:D.
课堂练习
2.如图,在平行四边形ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,他们相交于G,延长BE交CD的延长线于点H,则图中的相似三角形共有 对.
4
3.如图,在△ABC中,DE∥AB,BE=2,CE=6,AD=2.5,则AC的长为________.
10
4.如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则S四边形EHFG
÷S菱形ABCD的值为
【详解】解:∵BE=2AE,DF=2FC,∴,
∵G、H分别是AC的三等分点,∴,,∴,
∴EG∥BC∴,
同理可得HF∥AD,,∴ ,
1.通过本节课的学习,你学会了哪些知识?
2. 你还记得平行线分线段成比例定理及推论的内容吗?
3.简述判定两个三角形相似的方法?
课堂总结
1.课本P17练习1,2.1
2.习题1.2 T1
3. 平行线分线段成比例定理:
4. 平行线分线段成比例定理的推论:
作业布置
22
2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
