24.2.2 直线和圆的位置关系—九年级数学人教版上册课时优化训练(含答案)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系—九年级数学人教版上册课时优化训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 535.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 23:53:48 | ||
图片预览


文档简介
24.2.2 直线和圆的位置关系—九年级数学人教版上册课时优化训练
1.如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
A.以为半径的圆 B.以为半径的圆
C.以为半径的圆 D.以为半径的圆
2.已知的半径等于8cm,圆心O到直线l的距离为9cm,则直线l与的公共点的个数为( )
A.0 B.1
C.2 D.3个或3个以上
3.已知的半径为8 cm,圆心O到直线l上某点的距离为8 cm,则直线l与的公共点的个数为( )
A.0 B.1或0 C.0或2 D.1或2
4.在平面直角坐标系中,以点为圆心,2为半径作,下列判断正确的是( )
A.与x轴相交 B.与y轴相切
C.点O在外 D.点在内
5.如图,AB、AC、BD是的切线,切点分别是P、C、D.若,,则BD的长是( )
A.4 B.3 C.2 D.1
6.已知的半径是一元二次方程的一个根,圆心O到直线l的距离,则直线l与的位置关系是( )
A.相交 B.相切 C.相离或相切 D.相交或相切
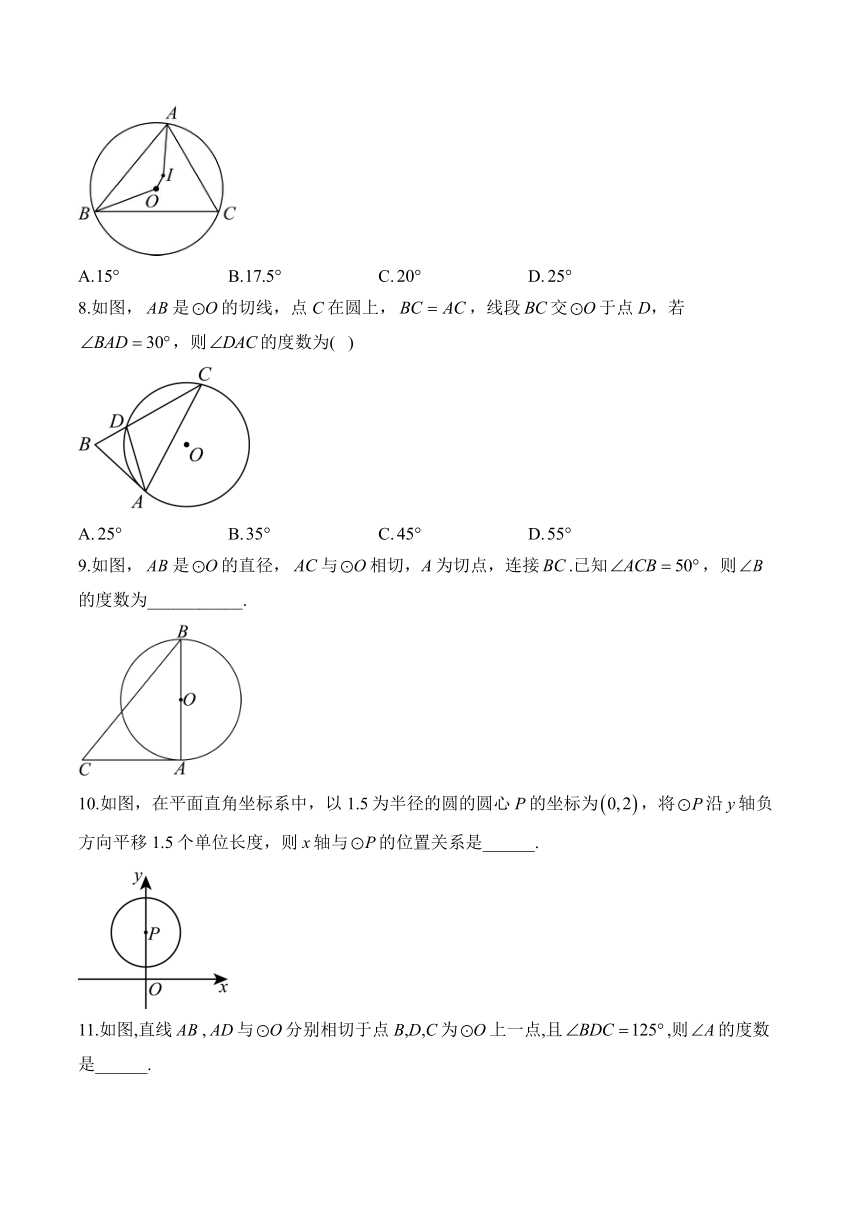
7.如图,点O是外接圆的圆心,点I是的内心,连接,.若,则的度数为( )
A. B. C. D.
8.如图,是的切线,点C在圆上,,线段交于点D,若,则的度数为( )
A. B. C. D.
9.如图,是的直径,与相切,A为切点,连接.已知,则的度数为___________.
10.如图,在平面直角坐标系中,以1.5为半径的圆的圆心P的坐标为,将沿y轴负方向平移1.5个单位长度,则x轴与的位置关系是______.
11.如图,直线,与分别相切于点B,D,C为上一点,且,则的度数是______.
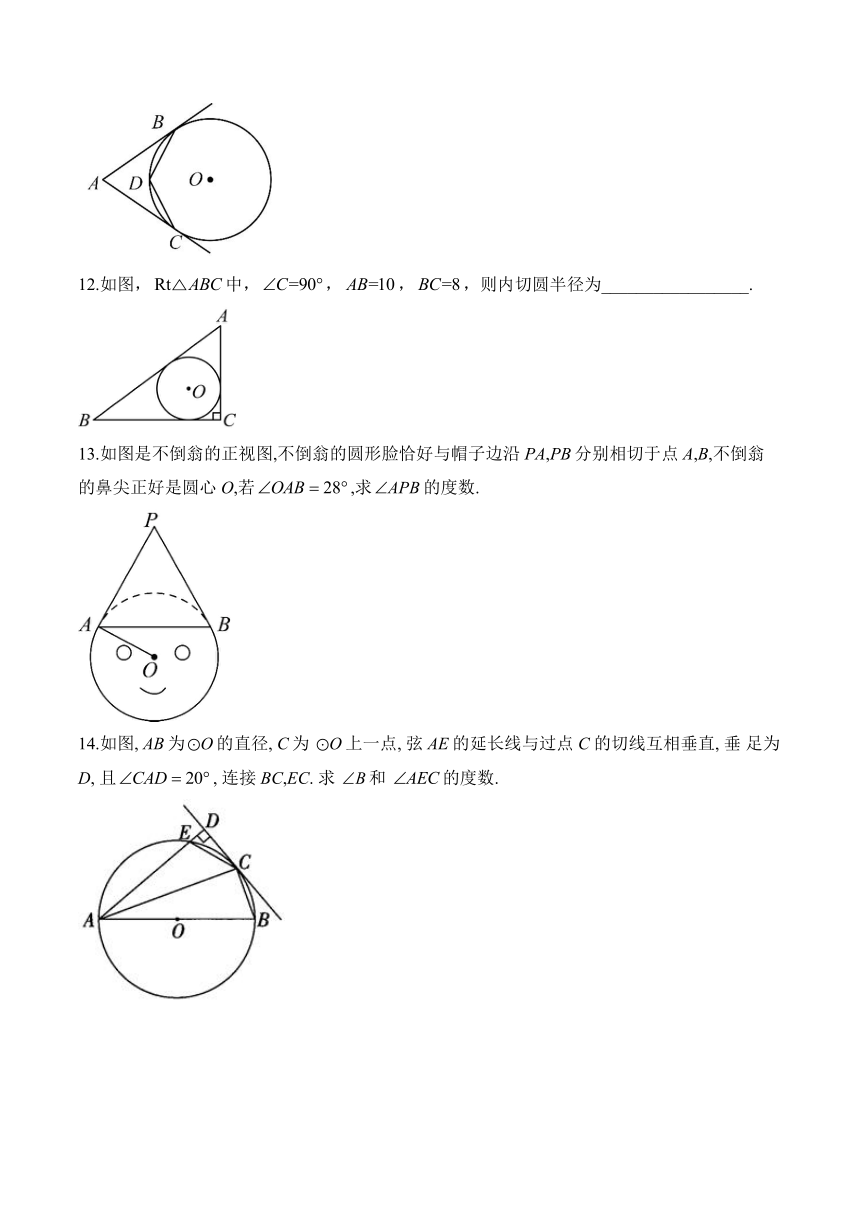
12.如图,中,,,,则内切圆半径为_________________.
13.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若,求的度数.
14.如图, AB为的直径, C为 上一点, 弦 AE的延长线与过点C 的切线互相垂直, 垂 足为D, 且, 连接BC,EC. 求 和 的度数.
答案以及解析
1.答案:B
解析:于B,
以点P为圆心,为半径的圆与直线l相切.
故选:B.
2.答案:A
解析:的半径等于r为8cm,圆心O到直线l的距离为d为9cm,
直线l与相离,
所以直线l与的公共点的个数为0,
故选A.
3.答案:D
解析:的半径为8 cm,圆心O到直线l上某点的距离为8 cm,
圆心O到直线l的距离小于或等于8 cm,
即圆心O到直线l的距离小于或等于圆的半径,
直线l和相切或相交,
直线l与有1个或2个公共点.
4.答案:C
解析:圆心,
到x轴的距离是3,到y轴的距离是1,
的半径为2,
与x轴相离,与y轴相交,故选项A、B错误;
由,
则点O在外,故选项C正确;
设,
,
则点在上,故选项D错误;
故选:C.
5.答案:C
解析:、为的切线,
,
、为的切线,
,
.
故选:C.
6.答案:D
解析:,
,,
的半径为一元二次方程的根,
或,
,
当时,,
直线l与的位置关系是相切,
当时,,
直线l与的位置关系是相交,
故选:D.
7.答案:C
解析:连接,
∵点I是的内心,,
∴,
∴,
∵,
∴,
故选:C.
8.答案:C
解析:连接并延长交于点E,连,
为的切线,为直径,
,
,
,
,
,
,
,
故选:C.
9.答案:/40度
解析:与相切,
,
又,
,
故答案为:.
10.答案:相交
解析:,
,
将沿y轴负方向平移1.5个单位长度后,,
,
平移后x轴与的位置关系是相交,
故答案为:相交.
11.答案:
解析:令优弧上任意一点E,连接,,,,
∵直线,与分别相切于点B,D,
∴,
∵,
∴,
∴,
∴,
故答案为:.
12.答案:2
解析:连接,,,
.
是的内切圆,
,,,,,,
四边形是正方形.
根据勾股定理.
设半径为r,则,
,则,
,则.
,
,
解得.
所以的半径为2.
故答案为:2.
13.答案:
解析:切于点A,OA是半径,
,
.
,
.
,PB分别切于点A,B,
,
.
,
.
14.答案:
解析:连接OC, 如图.
CD是 的切线,
又
,
,
,
AB 为 的直径,
,
1.如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
A.以为半径的圆 B.以为半径的圆
C.以为半径的圆 D.以为半径的圆
2.已知的半径等于8cm,圆心O到直线l的距离为9cm,则直线l与的公共点的个数为( )
A.0 B.1
C.2 D.3个或3个以上
3.已知的半径为8 cm,圆心O到直线l上某点的距离为8 cm,则直线l与的公共点的个数为( )
A.0 B.1或0 C.0或2 D.1或2
4.在平面直角坐标系中,以点为圆心,2为半径作,下列判断正确的是( )
A.与x轴相交 B.与y轴相切
C.点O在外 D.点在内
5.如图,AB、AC、BD是的切线,切点分别是P、C、D.若,,则BD的长是( )
A.4 B.3 C.2 D.1
6.已知的半径是一元二次方程的一个根,圆心O到直线l的距离,则直线l与的位置关系是( )
A.相交 B.相切 C.相离或相切 D.相交或相切
7.如图,点O是外接圆的圆心,点I是的内心,连接,.若,则的度数为( )
A. B. C. D.
8.如图,是的切线,点C在圆上,,线段交于点D,若,则的度数为( )
A. B. C. D.
9.如图,是的直径,与相切,A为切点,连接.已知,则的度数为___________.
10.如图,在平面直角坐标系中,以1.5为半径的圆的圆心P的坐标为,将沿y轴负方向平移1.5个单位长度,则x轴与的位置关系是______.
11.如图,直线,与分别相切于点B,D,C为上一点,且,则的度数是______.
12.如图,中,,,,则内切圆半径为_________________.
13.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若,求的度数.
14.如图, AB为的直径, C为 上一点, 弦 AE的延长线与过点C 的切线互相垂直, 垂 足为D, 且, 连接BC,EC. 求 和 的度数.
答案以及解析
1.答案:B
解析:于B,
以点P为圆心,为半径的圆与直线l相切.
故选:B.
2.答案:A
解析:的半径等于r为8cm,圆心O到直线l的距离为d为9cm,
直线l与相离,
所以直线l与的公共点的个数为0,
故选A.
3.答案:D
解析:的半径为8 cm,圆心O到直线l上某点的距离为8 cm,
圆心O到直线l的距离小于或等于8 cm,
即圆心O到直线l的距离小于或等于圆的半径,
直线l和相切或相交,
直线l与有1个或2个公共点.
4.答案:C
解析:圆心,
到x轴的距离是3,到y轴的距离是1,
的半径为2,
与x轴相离,与y轴相交,故选项A、B错误;
由,
则点O在外,故选项C正确;
设,
,
则点在上,故选项D错误;
故选:C.
5.答案:C
解析:、为的切线,
,
、为的切线,
,
.
故选:C.
6.答案:D
解析:,
,,
的半径为一元二次方程的根,
或,
,
当时,,
直线l与的位置关系是相切,
当时,,
直线l与的位置关系是相交,
故选:D.
7.答案:C
解析:连接,
∵点I是的内心,,
∴,
∴,
∵,
∴,
故选:C.
8.答案:C
解析:连接并延长交于点E,连,
为的切线,为直径,
,
,
,
,
,
,
,
故选:C.
9.答案:/40度
解析:与相切,
,
又,
,
故答案为:.
10.答案:相交
解析:,
,
将沿y轴负方向平移1.5个单位长度后,,
,
平移后x轴与的位置关系是相交,
故答案为:相交.
11.答案:
解析:令优弧上任意一点E,连接,,,,
∵直线,与分别相切于点B,D,
∴,
∵,
∴,
∴,
∴,
故答案为:.
12.答案:2
解析:连接,,,
.
是的内切圆,
,,,,,,
四边形是正方形.
根据勾股定理.
设半径为r,则,
,则,
,则.
,
,
解得.
所以的半径为2.
故答案为:2.
13.答案:
解析:切于点A,OA是半径,
,
.
,
.
,PB分别切于点A,B,
,
.
,
.
14.答案:
解析:连接OC, 如图.
CD是 的切线,
又
,
,
,
AB 为 的直径,
,
同课章节目录
