24.4 弧长和扇形面积—九年级数学人教版上册课时优化训练(含答案)
文档属性
| 名称 | 24.4 弧长和扇形面积—九年级数学人教版上册课时优化训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 902.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-20 23:55:47 | ||
图片预览


文档简介
24.4 弧长和扇形面积—九年级数学人教版上册课时优化训练
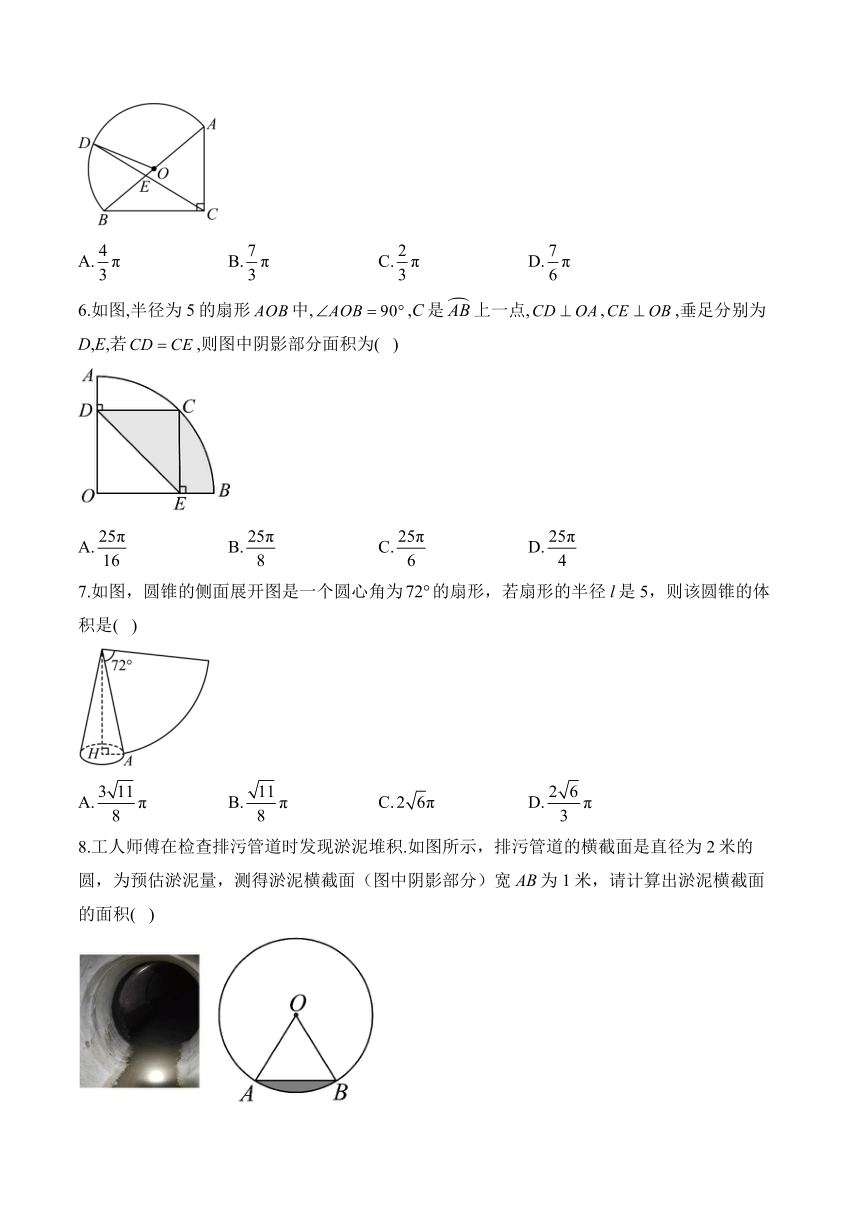
1.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧,点O是这段弧所在圆的圆心,半径,圆心角,则这段弯路的长度为( )
A. B. C. D.
2.如图,圆锥的底面半径为3,母线长为5,则其侧面积为( )
A. B. C. D.
3.一个扇形的弧长是,其圆心角是150°,此扇形的面积为( )
A. B. C. D.
4.如图,,,两两不相交,且半径都是.则图中三个阴影扇形的弧长之和为( )
A. B. C. D.
5.如图,在中,,,斜边是半圆O的直径,点D是半圆上的一个动点,连接与交于点E,若时,弧的长为( )
A. B. C. D.
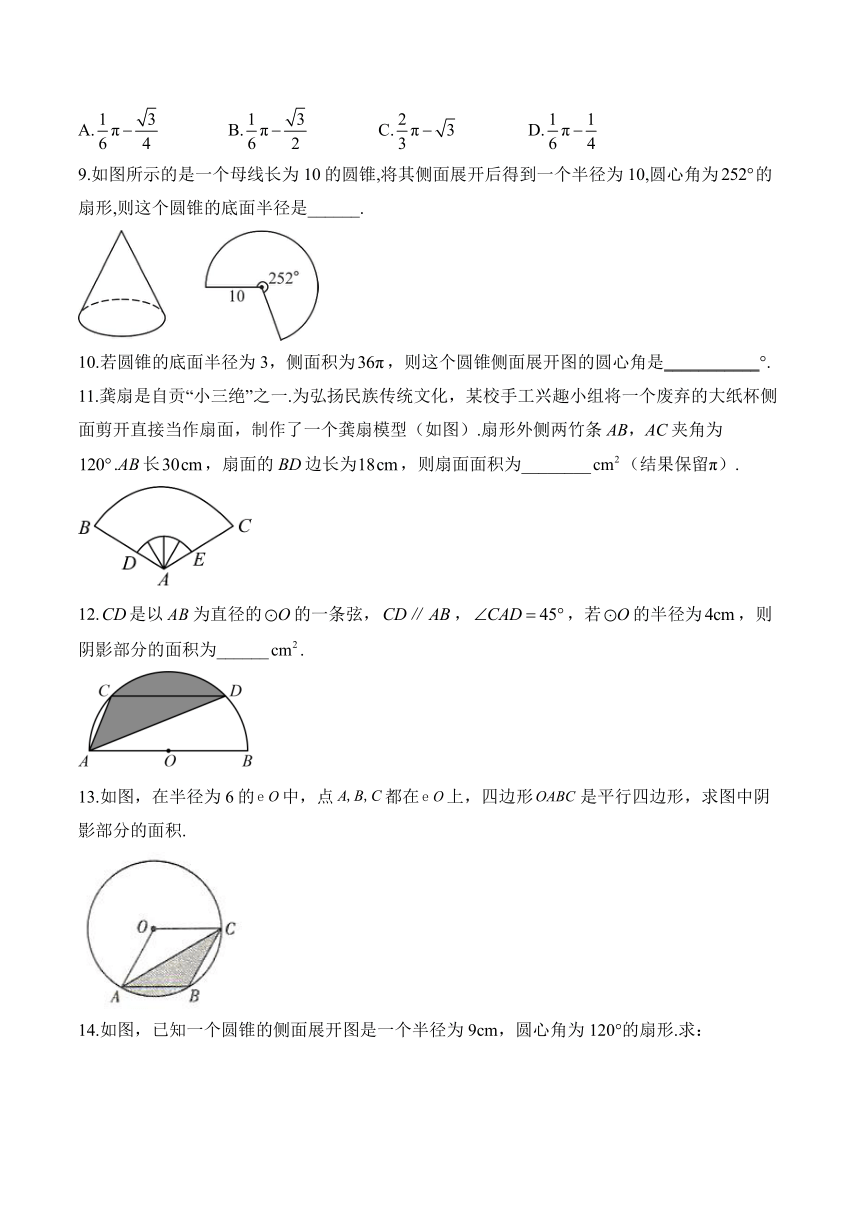
6.如图,半径为5的扇形中,,C是上一点,,,垂足分别为D,E,若,则图中阴影部分面积为( )
A. B. C. D.
7.如图,圆锥的侧面展开图是一个圆心角为的扇形,若扇形的半径l是5,则该圆锥的体积是( )
A. B. C. D.
8.工人师傅在检查排污管道时发现淤泥堆积.如图所示,排污管道的横截面是直径为2米的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽AB为1米,请计算出淤泥横截面的面积( )
A. B. C. D.
9.如图所示的是一个母线长为10的圆锥,将其侧面展开后得到一个半径为10,圆心角为的扇形,则这个圆锥的底面半径是______.
10.若圆锥的底面半径为3,侧面积为,则这个圆锥侧面展开图的圆心角是___________°.
11.龚扇是自贡“小三绝”之一.为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图).扇形外侧两竹条AB,AC夹角为.AB长,扇面的BD边长为,则扇面面积为________(结果保留π).
12.是以为直径的的一条弦,,,若的半径为,则阴影部分的面积为______.
13.如图,在半径为6的中,点都在上,四边形是平行四边形,求图中阴影部分的面积.
14.如图,已知一个圆锥的侧面展开图是一个半径为9cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
答案以及解析
1.答案:C
解析:因为半径,圆心角,所以这段弯路的长度为.
2.答案:D
解析:圆锥的底面半径为3,母线长为5,
圆锥的侧面积为:;
故选D.
3.答案:B
解析:该扇形的半径为:,
∴扇形的面积为:,
故选:B.
4.答案:B
解析:,
且,,两两不相交,且半径都是,
三个阴影扇形的弧长之和可以看作是圆心角为,
半径是的弧长,
三个阴影扇形的弧长之和为:,
故选:B.
5.答案:B
解析:如图,
,,
,
,
弧的长为,
故选:B.
6.答案:B
解析:如图所示,连接,
∵,,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,,
∴图中阴影部分面积,
故选:B.
7.答案:D
解析:设圆锥的半径为r,则圆锥的底面周长为,
圆锥的侧面展开图是一个圆心角为的扇形,且扇形的半径l是5,
扇形的弧长为,
圆锥的底面周长与侧面展开图扇形的弧长相等,
,
,
圆锥的高为,
圆锥的体积为,
故选:D.
8.答案:A
解析:过点O作于D,则,,
圆的直径为2米,,
在中,,
,为等边三角形,
,
淤泥横截面的面积,
故选:A.
9.答案:7
解析:设这个圆锥的底面半径为:r,
由题意可得:,
解得:,
故答案为:7.
10.答案:
解析:根据圆锥侧面积公式:,可得,
解得:,
,
解得,
侧面展开图的圆心角是.
故答案为:.
11.答案:
解析:扇面面积=扇形的面积-扇形的面积
,
故答案为:.
12.答案:
解析:如图所示,连接、,
,,
,
又,
,
阴影部分的面积扇形的面积,
故答案为:.
13.答案:连接,
四边形是平行四边形,,,
是等边三角形,
,,
图中阴影部分的面积.
解析:
14.答案:(1)圆锥的底面半径为3cm
(2)圆锥的全面积
解析:(1)设圆锥的底面半径为rcm.
扇形的弧长为,
,
解得,
圆锥的底面半径为3cm.
(2)圆锥的侧面积:.
园锥的底面积:.
圆锥的全面积.
1.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧,点O是这段弧所在圆的圆心,半径,圆心角,则这段弯路的长度为( )
A. B. C. D.
2.如图,圆锥的底面半径为3,母线长为5,则其侧面积为( )
A. B. C. D.
3.一个扇形的弧长是,其圆心角是150°,此扇形的面积为( )
A. B. C. D.
4.如图,,,两两不相交,且半径都是.则图中三个阴影扇形的弧长之和为( )
A. B. C. D.
5.如图,在中,,,斜边是半圆O的直径,点D是半圆上的一个动点,连接与交于点E,若时,弧的长为( )
A. B. C. D.
6.如图,半径为5的扇形中,,C是上一点,,,垂足分别为D,E,若,则图中阴影部分面积为( )
A. B. C. D.
7.如图,圆锥的侧面展开图是一个圆心角为的扇形,若扇形的半径l是5,则该圆锥的体积是( )
A. B. C. D.
8.工人师傅在检查排污管道时发现淤泥堆积.如图所示,排污管道的横截面是直径为2米的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽AB为1米,请计算出淤泥横截面的面积( )
A. B. C. D.
9.如图所示的是一个母线长为10的圆锥,将其侧面展开后得到一个半径为10,圆心角为的扇形,则这个圆锥的底面半径是______.
10.若圆锥的底面半径为3,侧面积为,则这个圆锥侧面展开图的圆心角是___________°.
11.龚扇是自贡“小三绝”之一.为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图).扇形外侧两竹条AB,AC夹角为.AB长,扇面的BD边长为,则扇面面积为________(结果保留π).
12.是以为直径的的一条弦,,,若的半径为,则阴影部分的面积为______.
13.如图,在半径为6的中,点都在上,四边形是平行四边形,求图中阴影部分的面积.
14.如图,已知一个圆锥的侧面展开图是一个半径为9cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
答案以及解析
1.答案:C
解析:因为半径,圆心角,所以这段弯路的长度为.
2.答案:D
解析:圆锥的底面半径为3,母线长为5,
圆锥的侧面积为:;
故选D.
3.答案:B
解析:该扇形的半径为:,
∴扇形的面积为:,
故选:B.
4.答案:B
解析:,
且,,两两不相交,且半径都是,
三个阴影扇形的弧长之和可以看作是圆心角为,
半径是的弧长,
三个阴影扇形的弧长之和为:,
故选:B.
5.答案:B
解析:如图,
,,
,
,
弧的长为,
故选:B.
6.答案:B
解析:如图所示,连接,
∵,,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,,
∴图中阴影部分面积,
故选:B.
7.答案:D
解析:设圆锥的半径为r,则圆锥的底面周长为,
圆锥的侧面展开图是一个圆心角为的扇形,且扇形的半径l是5,
扇形的弧长为,
圆锥的底面周长与侧面展开图扇形的弧长相等,
,
,
圆锥的高为,
圆锥的体积为,
故选:D.
8.答案:A
解析:过点O作于D,则,,
圆的直径为2米,,
在中,,
,为等边三角形,
,
淤泥横截面的面积,
故选:A.
9.答案:7
解析:设这个圆锥的底面半径为:r,
由题意可得:,
解得:,
故答案为:7.
10.答案:
解析:根据圆锥侧面积公式:,可得,
解得:,
,
解得,
侧面展开图的圆心角是.
故答案为:.
11.答案:
解析:扇面面积=扇形的面积-扇形的面积
,
故答案为:.
12.答案:
解析:如图所示,连接、,
,,
,
又,
,
阴影部分的面积扇形的面积,
故答案为:.
13.答案:连接,
四边形是平行四边形,,,
是等边三角形,
,,
图中阴影部分的面积.
解析:
14.答案:(1)圆锥的底面半径为3cm
(2)圆锥的全面积
解析:(1)设圆锥的底面半径为rcm.
扇形的弧长为,
,
解得,
圆锥的底面半径为3cm.
(2)圆锥的侧面积:.
园锥的底面积:.
圆锥的全面积.
同课章节目录
