2.4.2 合并同类项 课件(共25张PPT) 2024-2025学年华师大版七年级数学上册
文档属性
| 名称 | 2.4.2 合并同类项 课件(共25张PPT) 2024-2025学年华师大版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-29 10:37:31 | ||
图片预览







文档简介
(共25张PPT)
华师大版 七年级 上册
02
2.4.2 合并同类项
学习目标
1.掌握合并同类项的法则,并能准确合并同类项.
2.能在合并同类项的基础上进行化简、求值运算.
复习回顾
定义:所含字母相同,并且相同字母的指数都相等的项叫做同类项.
判断同类项的关键是“一相同”“一相等”“两无关”:
①“一相同”:所含字母完全相同;
②“一相等”:相同字母的指数都相等;
③“两无关”:与系数无关,与字母的排列顺序无关.
注意:所有的常数项都是同类项.
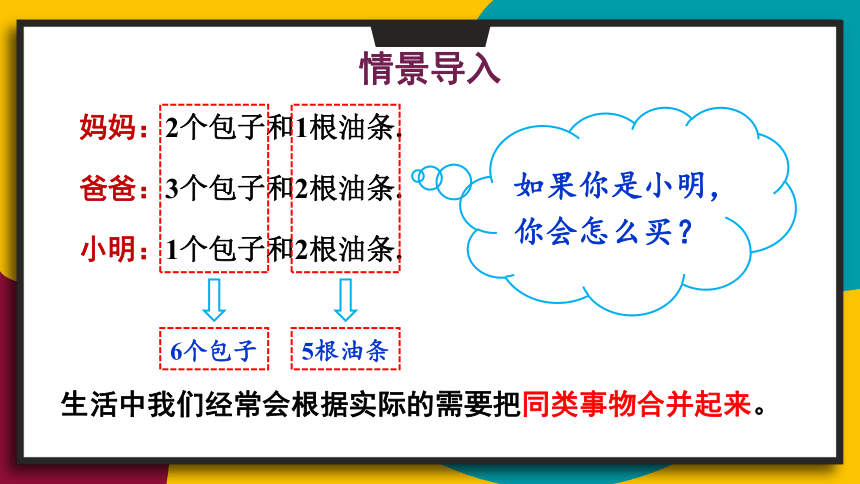
妈妈:2个包子和1根油条.
爸爸:3个包子和2根油条.
小明:1个包子和2根油条.
6个包子
5根油条
生活中我们经常会根据实际的需要把同类事物合并起来。
如果你是小明,你会怎么买?
情景导入
探索新知
1.运用运算律计算:8×2+5×2
=(8+5)×2=26.
2.类比数的运算,计算:3x2y+5x2y.
3x2y+5x2y
=(3+5)x2y
=8x2y
如果一个多项式中含有同类项,那么我们可以把同类项合并起来,使结果得以简化.
对多项式3x2y-4xy2-3+5x2y+2xy2+5进行合并:
3x2y-4xy2-3+5x2y+2xy2+5
=3x2y+5x2y-4xy2+2xy2-3+5
加法的交换律
=(3x2y+5x2y)+(-4xy2+2xy2)+(-3+5)
加法的结合律
=(3+5)x2y+(-4+2)xy2+(-3+5)
乘法的分配律
=8x2y-2xy2+2
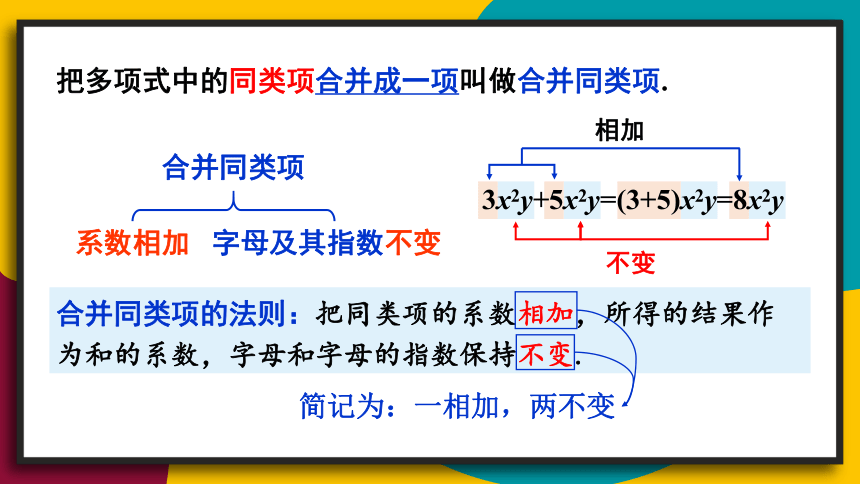
把多项式中的同类项合并成一项叫做合并同类项.
3x2y+5x2y=(3+5)x2y=8x2y
相加
不变
合并同类项
系数相加
字母及其指数不变
合并同类项的法则:把同类项的系数相加,所得的结果作为和的系数,字母和字母的指数保持不变.
简记为:一相加,两不变
例3
合并下列多项式中的同类项:
(1)2a2b-3a2b+
解:2a2b-3a2b+
三项都是同类项
(2)a3-a2b+ab2+a2b-ab2+b3
解:a3-a2b+ab2+a2b-ab2+b3
=a3 +(-a2b+a2b)+(ab2-ab2)+ b3
=a3+b3
=a3 +(-1+1)a2b +(1-1)ab2 + b3
合并同类项的步骤:
1.找出同类项,当项数较多时,用记号标出各同类项,注意每一项的符号;
2.根据加法的交换律和结合律,将同类项集中在一起;
3.根据合并同类项的法则合并同类项;
4.写出合并后的结果.
一找
二移
三合
四写
解:3x2+4x-2x2-x+x2-3x-1
例4
求多项式3x2+4x-2x2-x+x2-3x-1的值,其中x=-3.
先合并同类项
=(3-2+1)x2+(4-1-3)x-1
=2x2-1
当x=-3时,原式=2×(-3)2-1=17.
试一试,把x=-3直接代入多项式求值. 比较一下,哪个解法更简便?
先合并同类项,将多项式化简,再求值,比较简便.
例5
如图所示的窗框,上部分为半圆,下部分为6个大小一样的长方形,长方形的长与的比为3∶2. 如果长方形的长分别为0.4m、0.5m、0.6m等,那么窗框所需材料的长度分别是多少 如果长方形的长为 a m呢
a
a
a
a
解:我们不妨先解答最后一问,即:如果长方形的长为 a m,求窗框所需材料的长度.
如果长方形的长为a m,那么它的宽为 a m.由图不难知道,窗框所需材料的长度为
=(9+6+π)a
=(15+π)a(m).
a
a
要解答第一问,只需分别将a=0.4、0.5、0.6等代入上式求值即可.
例如当长方形的长为0.4m时,求窗框所需材料的长度(要求精确到0.1m,π取3.14),有
(15+π)a
≈(15+3.14)×0.4
=18.14×0.4
=7.256
≈7.3(m).
所以,当长方形的长为 0.4m时,窗框所需材料的长度约为7.3m.
a
a
当a=0.5时,
(15+π)a
≈(15+3.14)×0.5
=18.14×0.5
=9.07
≈9.1(m).
当a=0.6时,
(15+π)a
≈(15+3.14)×0.6
=18.14×0.6
=10.884
≈10.9(m).
所以,当长方形的长为 0.5m时,窗框所需材料的长度约为9.1m;当长方形的长为 0.6m时,窗框所需材料的长度约为10.9m.
随堂练习
1.如果两个同类项的系数互为相反数,那么合并同类项后,结果是______.
0
2.下列等式成立的是( )
A.3a+2b=5ab B.a2+2a2=3a4
C.5y3-3y3=2y3 D.3x3-x2=2x
C
【选自教材P105 练习 第1题】
3.先标出下列各多项式中的同类项,再合并同类项:
(1)3x-2x2+5+3x2-2x-5
解:3x-2x2+5+3x2-2x-5
=3x-2x-2x2+3x2+5-5
=(3-2)x+(-2+3)x2+(5-5)
=x+x2
【选自教材P105 练习 第2题】
(2)a3+a2b+ab2-a2b-ab2-b3
(3) 6a2-5b2+2ab+5b2-6a2
解:a3+a2b+ab2-a2b-ab2-b3
=a3+a2b-a2b+ab2-ab2-b3
=a3+(a2b-a2b)+(ab2-ab2)-b3
=a3-b3
解:6a2-5b2+2ab+5b2-6a2
=6a2-6a2-5b2+5b2+2ab
=(6-6)a2+(-5+5)b2+2ab
=2ab
4.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
(1)解: 7x2-3x2-2x-2x2+5+6x
=7x2-3x2-2x2-2x+6x+5
=(7-3-2)x2+(-2+6)x+5
=2x2+4x+5
当x=-2时,原式=2×(-2)2+4×(-2)+5=5.
【选自教材P105 练习 第3题】
(2)解:5a-2b+3b-4a-1
=5a-4a-2b+3b-1
=(5-4)a+(-2+3)b-1
=a+b-1
当a=-1, b=2时,原式=(-1)+2-1=0.
4.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
【选自教材P105 练习 第3题】
(3)解:2x2-3xy+y2-2xy-2x2+5xy -2y+1
=2x2-2x2-3xy-2xy+5xy+y2-2y+1
=(2-2)x2+(-3-2+5)xy+y2-2y+1
=y2-2y+1
当x = ,y =-1时,原式=(-1)2-2×(-1)+1=4.
4.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
【选自教材P105 练习 第3题】
5.某环保组织有三个工作组,这三个组参加了植树造林活动,其中甲组植树x棵,乙组的植树棵数比甲组的2倍少5,丙组的植树棵数比甲组的一半多10.
(1)这三个组一共植树多少棵
(2)当甲组植树40棵时,这三个组一共植树多少棵
解:(1)根据题意,得乙组植树(2x-5)棵,丙组植树 ( x+10)棵,
所以这三个组一共植树x+2x-5+ x+10=(1+2+ )x+(-5+10)= x+5(棵).
(2)当x=40时, x+5= ×40+5=145(棵),所以这三个组一共植树145棵.
课堂小结
同类项
①“一相同”:所含字母完全相同;
②“一相等”:相同字母的指数都相等;
③“两无关”:与系数无关,与字母的排列顺序无关.
合并同类项
①系数相加
②字母及其指数不变
一找
二移
三合
四写
步骤
法则
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
华师大版 七年级 上册
02
2.4.2 合并同类项
学习目标
1.掌握合并同类项的法则,并能准确合并同类项.
2.能在合并同类项的基础上进行化简、求值运算.
复习回顾
定义:所含字母相同,并且相同字母的指数都相等的项叫做同类项.
判断同类项的关键是“一相同”“一相等”“两无关”:
①“一相同”:所含字母完全相同;
②“一相等”:相同字母的指数都相等;
③“两无关”:与系数无关,与字母的排列顺序无关.
注意:所有的常数项都是同类项.
妈妈:2个包子和1根油条.
爸爸:3个包子和2根油条.
小明:1个包子和2根油条.
6个包子
5根油条
生活中我们经常会根据实际的需要把同类事物合并起来。
如果你是小明,你会怎么买?
情景导入
探索新知
1.运用运算律计算:8×2+5×2
=(8+5)×2=26.
2.类比数的运算,计算:3x2y+5x2y.
3x2y+5x2y
=(3+5)x2y
=8x2y
如果一个多项式中含有同类项,那么我们可以把同类项合并起来,使结果得以简化.
对多项式3x2y-4xy2-3+5x2y+2xy2+5进行合并:
3x2y-4xy2-3+5x2y+2xy2+5
=3x2y+5x2y-4xy2+2xy2-3+5
加法的交换律
=(3x2y+5x2y)+(-4xy2+2xy2)+(-3+5)
加法的结合律
=(3+5)x2y+(-4+2)xy2+(-3+5)
乘法的分配律
=8x2y-2xy2+2
把多项式中的同类项合并成一项叫做合并同类项.
3x2y+5x2y=(3+5)x2y=8x2y
相加
不变
合并同类项
系数相加
字母及其指数不变
合并同类项的法则:把同类项的系数相加,所得的结果作为和的系数,字母和字母的指数保持不变.
简记为:一相加,两不变
例3
合并下列多项式中的同类项:
(1)2a2b-3a2b+
解:2a2b-3a2b+
三项都是同类项
(2)a3-a2b+ab2+a2b-ab2+b3
解:a3-a2b+ab2+a2b-ab2+b3
=a3 +(-a2b+a2b)+(ab2-ab2)+ b3
=a3+b3
=a3 +(-1+1)a2b +(1-1)ab2 + b3
合并同类项的步骤:
1.找出同类项,当项数较多时,用记号标出各同类项,注意每一项的符号;
2.根据加法的交换律和结合律,将同类项集中在一起;
3.根据合并同类项的法则合并同类项;
4.写出合并后的结果.
一找
二移
三合
四写
解:3x2+4x-2x2-x+x2-3x-1
例4
求多项式3x2+4x-2x2-x+x2-3x-1的值,其中x=-3.
先合并同类项
=(3-2+1)x2+(4-1-3)x-1
=2x2-1
当x=-3时,原式=2×(-3)2-1=17.
试一试,把x=-3直接代入多项式求值. 比较一下,哪个解法更简便?
先合并同类项,将多项式化简,再求值,比较简便.
例5
如图所示的窗框,上部分为半圆,下部分为6个大小一样的长方形,长方形的长与的比为3∶2. 如果长方形的长分别为0.4m、0.5m、0.6m等,那么窗框所需材料的长度分别是多少 如果长方形的长为 a m呢
a
a
a
a
解:我们不妨先解答最后一问,即:如果长方形的长为 a m,求窗框所需材料的长度.
如果长方形的长为a m,那么它的宽为 a m.由图不难知道,窗框所需材料的长度为
=(9+6+π)a
=(15+π)a(m).
a
a
要解答第一问,只需分别将a=0.4、0.5、0.6等代入上式求值即可.
例如当长方形的长为0.4m时,求窗框所需材料的长度(要求精确到0.1m,π取3.14),有
(15+π)a
≈(15+3.14)×0.4
=18.14×0.4
=7.256
≈7.3(m).
所以,当长方形的长为 0.4m时,窗框所需材料的长度约为7.3m.
a
a
当a=0.5时,
(15+π)a
≈(15+3.14)×0.5
=18.14×0.5
=9.07
≈9.1(m).
当a=0.6时,
(15+π)a
≈(15+3.14)×0.6
=18.14×0.6
=10.884
≈10.9(m).
所以,当长方形的长为 0.5m时,窗框所需材料的长度约为9.1m;当长方形的长为 0.6m时,窗框所需材料的长度约为10.9m.
随堂练习
1.如果两个同类项的系数互为相反数,那么合并同类项后,结果是______.
0
2.下列等式成立的是( )
A.3a+2b=5ab B.a2+2a2=3a4
C.5y3-3y3=2y3 D.3x3-x2=2x
C
【选自教材P105 练习 第1题】
3.先标出下列各多项式中的同类项,再合并同类项:
(1)3x-2x2+5+3x2-2x-5
解:3x-2x2+5+3x2-2x-5
=3x-2x-2x2+3x2+5-5
=(3-2)x+(-2+3)x2+(5-5)
=x+x2
【选自教材P105 练习 第2题】
(2)a3+a2b+ab2-a2b-ab2-b3
(3) 6a2-5b2+2ab+5b2-6a2
解:a3+a2b+ab2-a2b-ab2-b3
=a3+a2b-a2b+ab2-ab2-b3
=a3+(a2b-a2b)+(ab2-ab2)-b3
=a3-b3
解:6a2-5b2+2ab+5b2-6a2
=6a2-6a2-5b2+5b2+2ab
=(6-6)a2+(-5+5)b2+2ab
=2ab
4.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
(1)解: 7x2-3x2-2x-2x2+5+6x
=7x2-3x2-2x2-2x+6x+5
=(7-3-2)x2+(-2+6)x+5
=2x2+4x+5
当x=-2时,原式=2×(-2)2+4×(-2)+5=5.
【选自教材P105 练习 第3题】
(2)解:5a-2b+3b-4a-1
=5a-4a-2b+3b-1
=(5-4)a+(-2+3)b-1
=a+b-1
当a=-1, b=2时,原式=(-1)+2-1=0.
4.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
【选自教材P105 练习 第3题】
(3)解:2x2-3xy+y2-2xy-2x2+5xy -2y+1
=2x2-2x2-3xy-2xy+5xy+y2-2y+1
=(2-2)x2+(-3-2+5)xy+y2-2y+1
=y2-2y+1
当x = ,y =-1时,原式=(-1)2-2×(-1)+1=4.
4.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
【选自教材P105 练习 第3题】
5.某环保组织有三个工作组,这三个组参加了植树造林活动,其中甲组植树x棵,乙组的植树棵数比甲组的2倍少5,丙组的植树棵数比甲组的一半多10.
(1)这三个组一共植树多少棵
(2)当甲组植树40棵时,这三个组一共植树多少棵
解:(1)根据题意,得乙组植树(2x-5)棵,丙组植树 ( x+10)棵,
所以这三个组一共植树x+2x-5+ x+10=(1+2+ )x+(-5+10)= x+5(棵).
(2)当x=40时, x+5= ×40+5=145(棵),所以这三个组一共植树145棵.
课堂小结
同类项
①“一相同”:所含字母完全相同;
②“一相等”:相同字母的指数都相等;
③“两无关”:与系数无关,与字母的排列顺序无关.
合并同类项
①系数相加
②字母及其指数不变
一找
二移
三合
四写
步骤
法则
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
