四川省成都市金堂中学2024-2025学年高一新生入学分班质量检测试题(含答案)
文档属性
| 名称 | 四川省成都市金堂中学2024-2025学年高一新生入学分班质量检测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 880.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 13:53:15 | ||
图片预览


文档简介
2024-2025学年四川省成都市金堂中学高一新生入学分班质量检测试题
题号 一 二 三 四 五 总分
得分
批阅人
A卷(100分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)计算的结果是( )
A.16 B.4 C.2 D.-4
2、(4分)下面是任意抛掷一枚质地均匀的正六面体骰子所得结果,其中发生的可能性很大的是( )
A.朝上的点数为 B.朝上的点数为
C.朝上的点数为的倍数 D.朝上的点数不小于
3、(4分)在正方形中,是边上一点,若,且点与点不重合,则的长可以是( )
A.3 B.4 C.5 D.6
4、(4分)如图,在梯形ABCD中,AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于( )cm
A.10 B.13 C.20 D.26
5、(4分)下列等式不一定成立的是( )
A. B.
C. D.
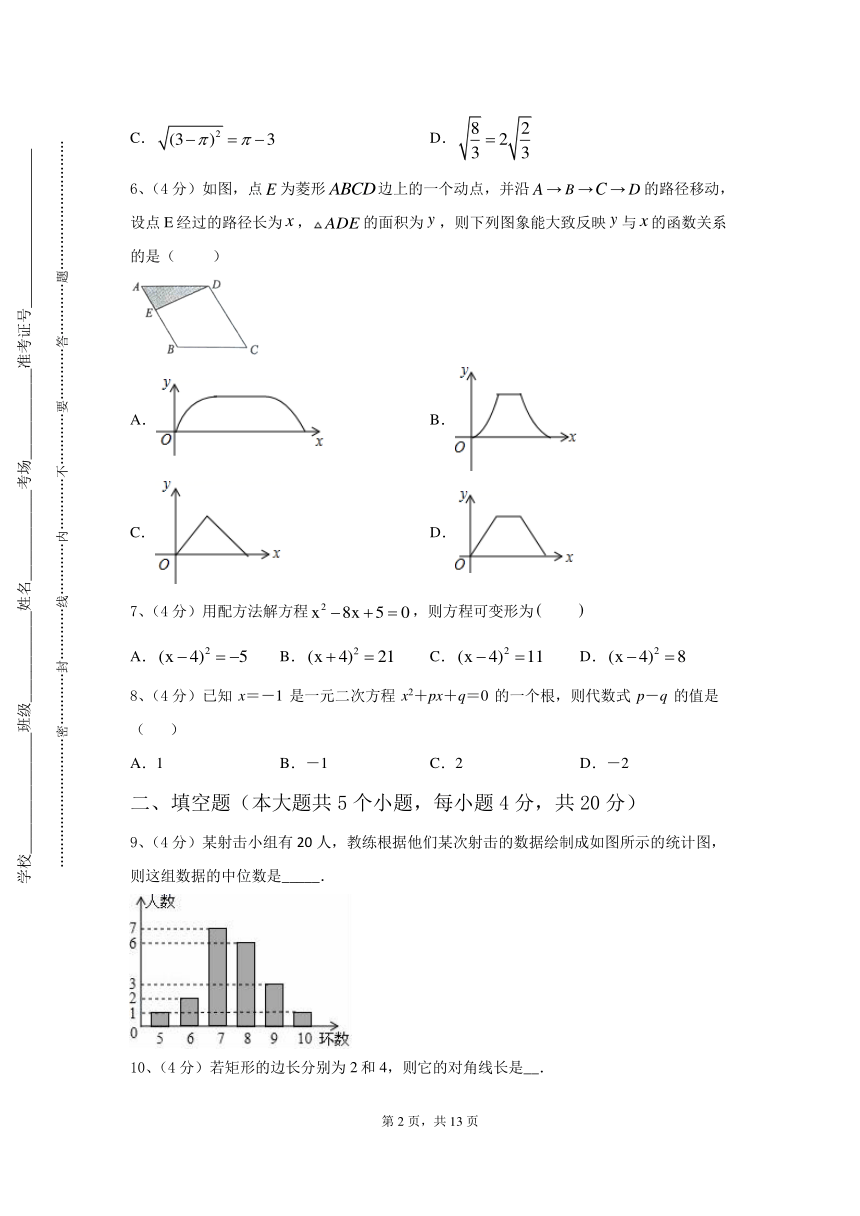
6、(4分)如图,点为菱形边上的一个动点,并沿→→→的路径移动,设点E经过的路径长为,的面积为,则下列图象能大致反映与的函数关系的是( )
A. B.
C. D.
7、(4分)用配方法解方程,则方程可变形为
A. B. C. D.
8、(4分)已知 x=-1 是一元二次方程 x2+px+q=0 的一个根,则代数式 p-q 的值是( )
A.1 B.-1 C.2 D.-2
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的中位数是_____.
10、(4分)若矩形的边长分别为2和4,则它的对角线长是__.
11、(4分)小华用S2={(x1-8)2+(x2-8)2+……+(x10-8)2计算一组数据的方差,那么x1+x2+x3+…+x10=____________.
12、(4分)当x=________时,分式的值为零.
13、(4分)如图,在中,为边延长线上一点,且,连结、.若的面积为1,则的面积为____.
三、解答题(本大题共5个小题,共48分)
14、(12分)某八年级计划用360元购买笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,结果买得的笔记本比打折前多10本。
(1)请求出每本笔记本的原来标价;
(2)恰逢文具店周年志庆,每本笔记本可以按原价打8折,这样该校最多可购入多少本笔记本?
15、(8分)如图,在中,为的中点,,.动点从点出发,沿方向以的速度向点运动;同时动点从点出发,沿方向以的速度向点运动,运动时间是秒.
(1)用含的代数式表示的长度.
(2)在运动过程中,是否存在某一时刻,使点位于线段的垂直平分线上?若存在,求出的值;若不存在,请说明理由.
(3)是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
(4)是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
16、(8分)先化简再求值:()÷,其中x=11﹣.
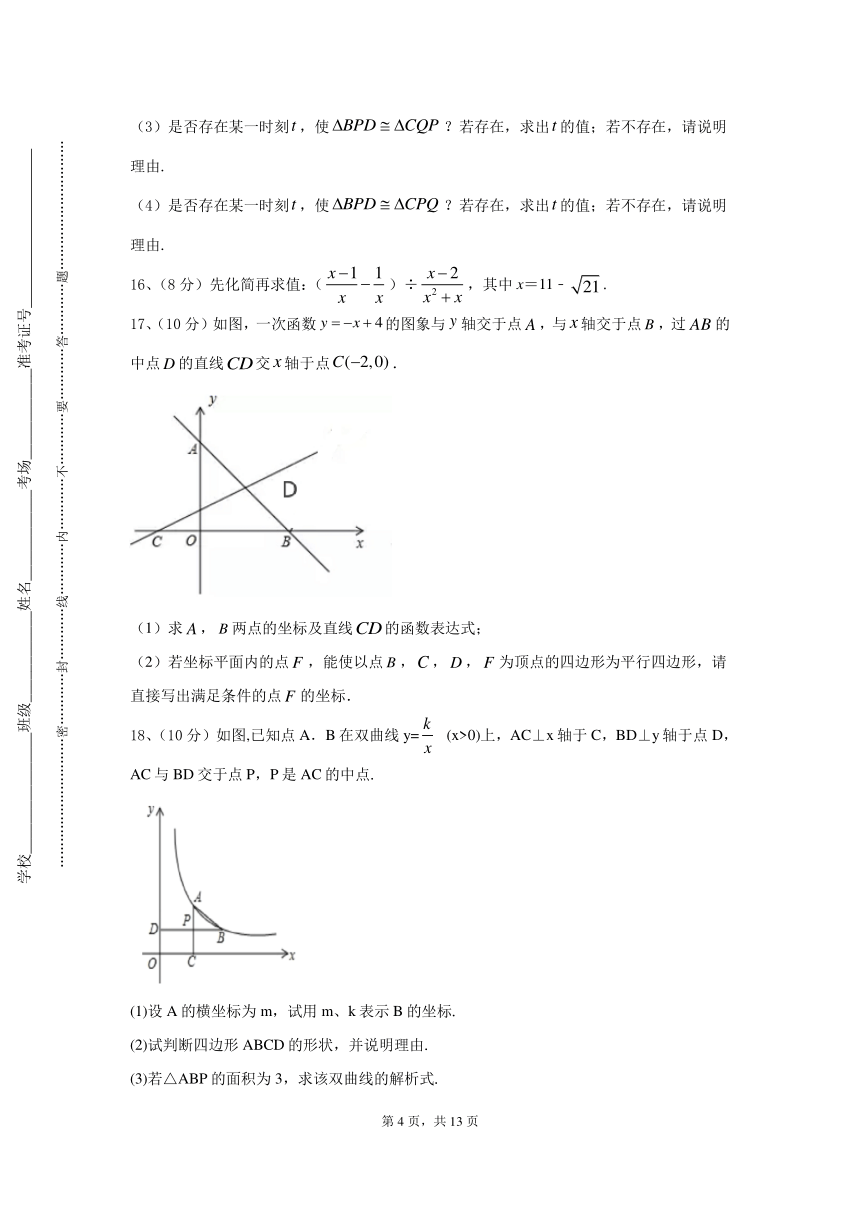
17、(10分)如图,一次函数的图象与轴交于点,与轴交于点,过的中点的直线交轴于点.
(1)求,两点的坐标及直线的函数表达式;
(2)若坐标平面内的点,能使以点,,,为顶点的四边形为平行四边形,请直接写出满足条件的点的坐标.
18、(10分)如图,已知点A.B在双曲线y= (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
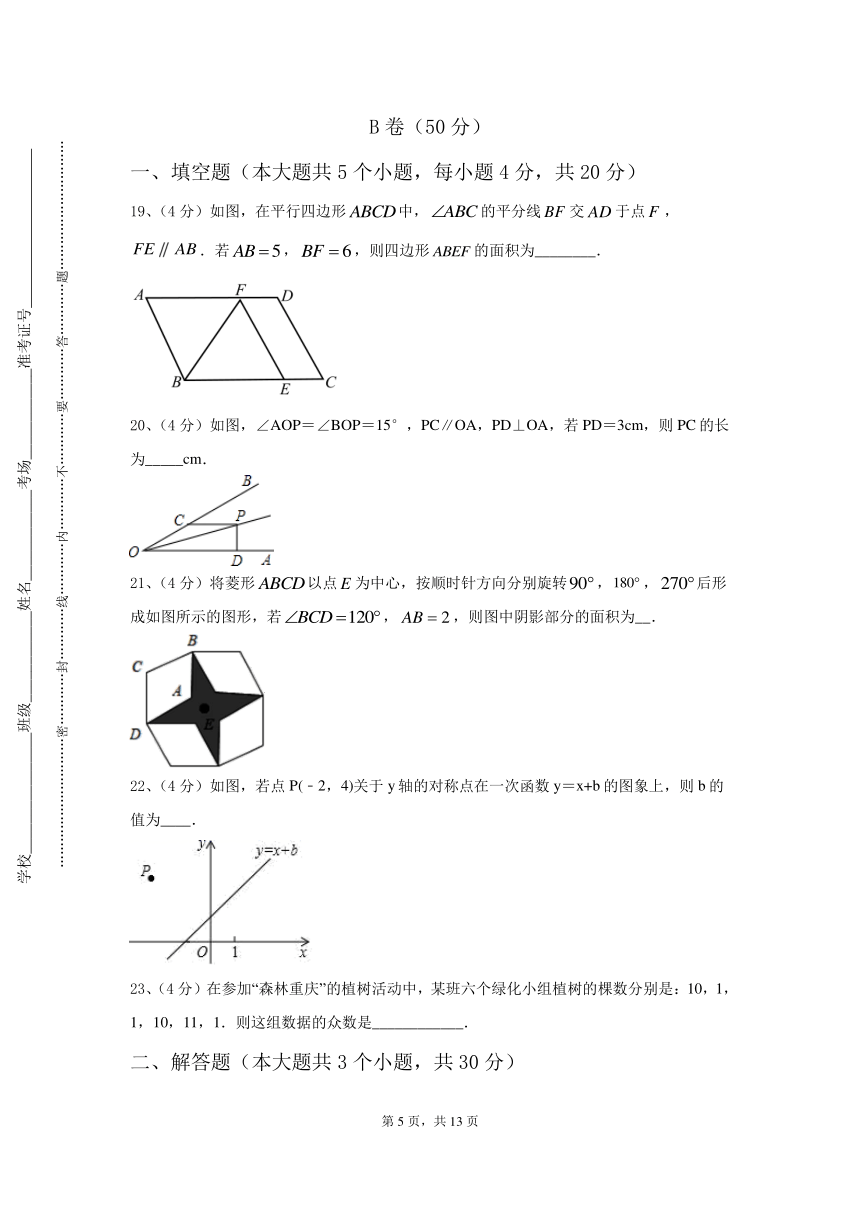
19、(4分)如图,在平行四边形中,的平分线交于点,.若,,则四边形的面积为________.
20、(4分)如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=3cm,则PC的长为_____cm.
21、(4分)将菱形以点为中心,按顺时针方向分别旋转,,后形成如图所示的图形,若,,则图中阴影部分的面积为__.
22、(4分)如图,若点P(﹣2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值为____.
23、(4分)在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.
二、解答题(本大题共3个小题,共30分)
24、(8分) “端午节小长假”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)甲公司每小时的租费是 元;
(2)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数解析式;
(3)请你帮助小明计算并分析选择哪个出游方案合算.
25、(10分)已知,直线与双曲线交于点,点.
(1)求反比例函数的表达式;
(2)根据图象直接写出不等式的解集 .
(3)将直线沿轴向下平移后,分别与轴,轴交于点,点,当四边形为平行四边形时,求直线的表达式.
26、(12分)如图,在矩形中,.
(1)请用尺规作图法,在矩形中作出以为对角线的菱形,且点分别在上.(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求菱形的边长.
参考答案
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、B
2、D
3、B
4、D
5、B
6、D
7、C
8、A
二、填空题(本大题共5个小题,每小题4分,共20分)
9、7.5
10、2.
11、1
12、3
13、3
三、解答题(本大题共5个小题,共48分)
14、解:(1)设笔记本打折前售价为元,则打折后售价为元,
由题意得:,
解得:,
经检验,是原方程的根.
答:打折前每本笔记本的售价是4元;
(2)购入笔记本的数量为:(元).
故该校最多可购入112本笔记本.
15、解:(1);
(2)若点位于线段的垂直平分线上,
则,
即,
解得.
所以存在,秒时点位于线段的垂直平分线上.
(3)若,
因为,,
所以只需,
即,解得,
所以存在.
(4)若,
因为,
所以需满足且,
即且,
所以不存在.
16、原式=,
当x=11﹣时,原式=11﹣ +1=12﹣.
本题主要考查分式的混合运算,解题的关键是熟练掌握分式混合运算顺序和运算法则.
17、解:(1)一次函数,令,则;
令,则,∴,,
∵是的中点,
∴,
设直线的函数表达式为,则
解得
∴直线的函数表达式为.
(2)①若四边形BCDF是平行四边形,则DF∥CB,DF=CB,
而点C向右平移6个单位长度得到点B,
∴点D向右平移6个单位长度得到点F(8,2);
②若四边形BCFD是平行四边形,则DF∥CB,DF=CB,
而点B向左平移6个单位长度得到点C,
∴点D向左平移6个单位长度得到点F(-4,2);
③若四边形BDCF是平行四边形,则BF∥DC,BF=DC,
而点D向左平移4个单位长度、向下平移2个单位长度得到点C,
∴点B向左平移4个单位长度、向下平移2个单位长度得到点F(0,-2);
综上,点的坐标为或或.
18、(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
∴点B的横坐标是2m.
又∵点B在双曲线y= (x>0)上,
∴B(2m,).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m, ),B(2m, ),
∴P(m, ),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为 BP AP=3,
∴BP AP=1,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A. B都在双曲线y= (x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OC AC=BP 2AP=12.
∴该双曲线的解析式是:y= .
一、填空题(本大题共5个小题,每小题4分,共20分)
19、1
20、1
21、
22、1
23、1
二、解答题(本大题共3个小题,共30分)
24、(1)由图象可得:甲公司每小时的租费是15元;
故答案为:15;
(2)设y1=k1x+80,
把点(1,95)代入,可得
95=k1+80,
解得k1=15,
∴y1=15x+80(x≥0);
设y2=k2x,
把(1,30)代入,可得
30=k2,即k2=30,
∴y2=30x(x≥0);
(3)当y1=y2时,15x+80=30x,
解得x=;
当y1>y2时,15x+80>30x,
解得x<;
当y1<y2时,15x+80<30x,
解得x>;
∴当租车时间为小时,选择甲乙公司一样合算;当租车时间小于小时,选择乙公司合算;当租车时间大于小时,选择甲公司合算.
25、解:(1)根据题意,可得点
将其代入反比例函数解析式,即得
(2)根据题意,得
解得
∴点B(4,-2)
∴直接观察图像,可得的解集为
或
(3)过点作轴,过点作轴,交于点
根据题意,可得
∴∠EAB=∠NOB=∠OCD,∠AEB=∠COD=90°,AB=CD
∴∠ABE=∠CDO
∴(ASA)
∴
则可得出直线CD为
此题主要考查一次函数、反比例函数和平行四边形的综合应用,熟练运用,即可解题.
26、 (1)连接BD,作BD的垂直平分线交AD、BC与E、F,连接BE,DF即可,如图,菱形即为所求.
(2)设的长为,
∵,
∴,
∴在中,,
即,
解得,即菱形的边长为.
第12页,共13页
题号 一 二 三 四 五 总分
得分
批阅人
A卷(100分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)计算的结果是( )
A.16 B.4 C.2 D.-4
2、(4分)下面是任意抛掷一枚质地均匀的正六面体骰子所得结果,其中发生的可能性很大的是( )
A.朝上的点数为 B.朝上的点数为
C.朝上的点数为的倍数 D.朝上的点数不小于
3、(4分)在正方形中,是边上一点,若,且点与点不重合,则的长可以是( )
A.3 B.4 C.5 D.6
4、(4分)如图,在梯形ABCD中,AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于( )cm
A.10 B.13 C.20 D.26
5、(4分)下列等式不一定成立的是( )
A. B.
C. D.
6、(4分)如图,点为菱形边上的一个动点,并沿→→→的路径移动,设点E经过的路径长为,的面积为,则下列图象能大致反映与的函数关系的是( )
A. B.
C. D.
7、(4分)用配方法解方程,则方程可变形为
A. B. C. D.
8、(4分)已知 x=-1 是一元二次方程 x2+px+q=0 的一个根,则代数式 p-q 的值是( )
A.1 B.-1 C.2 D.-2
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的中位数是_____.
10、(4分)若矩形的边长分别为2和4,则它的对角线长是__.
11、(4分)小华用S2={(x1-8)2+(x2-8)2+……+(x10-8)2计算一组数据的方差,那么x1+x2+x3+…+x10=____________.
12、(4分)当x=________时,分式的值为零.
13、(4分)如图,在中,为边延长线上一点,且,连结、.若的面积为1,则的面积为____.
三、解答题(本大题共5个小题,共48分)
14、(12分)某八年级计划用360元购买笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,结果买得的笔记本比打折前多10本。
(1)请求出每本笔记本的原来标价;
(2)恰逢文具店周年志庆,每本笔记本可以按原价打8折,这样该校最多可购入多少本笔记本?
15、(8分)如图,在中,为的中点,,.动点从点出发,沿方向以的速度向点运动;同时动点从点出发,沿方向以的速度向点运动,运动时间是秒.
(1)用含的代数式表示的长度.
(2)在运动过程中,是否存在某一时刻,使点位于线段的垂直平分线上?若存在,求出的值;若不存在,请说明理由.
(3)是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
(4)是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
16、(8分)先化简再求值:()÷,其中x=11﹣.
17、(10分)如图,一次函数的图象与轴交于点,与轴交于点,过的中点的直线交轴于点.
(1)求,两点的坐标及直线的函数表达式;
(2)若坐标平面内的点,能使以点,,,为顶点的四边形为平行四边形,请直接写出满足条件的点的坐标.
18、(10分)如图,已知点A.B在双曲线y= (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)如图,在平行四边形中,的平分线交于点,.若,,则四边形的面积为________.
20、(4分)如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=3cm,则PC的长为_____cm.
21、(4分)将菱形以点为中心,按顺时针方向分别旋转,,后形成如图所示的图形,若,,则图中阴影部分的面积为__.
22、(4分)如图,若点P(﹣2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值为____.
23、(4分)在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.
二、解答题(本大题共3个小题,共30分)
24、(8分) “端午节小长假”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)甲公司每小时的租费是 元;
(2)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数解析式;
(3)请你帮助小明计算并分析选择哪个出游方案合算.
25、(10分)已知,直线与双曲线交于点,点.
(1)求反比例函数的表达式;
(2)根据图象直接写出不等式的解集 .
(3)将直线沿轴向下平移后,分别与轴,轴交于点,点,当四边形为平行四边形时,求直线的表达式.
26、(12分)如图,在矩形中,.
(1)请用尺规作图法,在矩形中作出以为对角线的菱形,且点分别在上.(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求菱形的边长.
参考答案
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、B
2、D
3、B
4、D
5、B
6、D
7、C
8、A
二、填空题(本大题共5个小题,每小题4分,共20分)
9、7.5
10、2.
11、1
12、3
13、3
三、解答题(本大题共5个小题,共48分)
14、解:(1)设笔记本打折前售价为元,则打折后售价为元,
由题意得:,
解得:,
经检验,是原方程的根.
答:打折前每本笔记本的售价是4元;
(2)购入笔记本的数量为:(元).
故该校最多可购入112本笔记本.
15、解:(1);
(2)若点位于线段的垂直平分线上,
则,
即,
解得.
所以存在,秒时点位于线段的垂直平分线上.
(3)若,
因为,,
所以只需,
即,解得,
所以存在.
(4)若,
因为,
所以需满足且,
即且,
所以不存在.
16、原式=,
当x=11﹣时,原式=11﹣ +1=12﹣.
本题主要考查分式的混合运算,解题的关键是熟练掌握分式混合运算顺序和运算法则.
17、解:(1)一次函数,令,则;
令,则,∴,,
∵是的中点,
∴,
设直线的函数表达式为,则
解得
∴直线的函数表达式为.
(2)①若四边形BCDF是平行四边形,则DF∥CB,DF=CB,
而点C向右平移6个单位长度得到点B,
∴点D向右平移6个单位长度得到点F(8,2);
②若四边形BCFD是平行四边形,则DF∥CB,DF=CB,
而点B向左平移6个单位长度得到点C,
∴点D向左平移6个单位长度得到点F(-4,2);
③若四边形BDCF是平行四边形,则BF∥DC,BF=DC,
而点D向左平移4个单位长度、向下平移2个单位长度得到点C,
∴点B向左平移4个单位长度、向下平移2个单位长度得到点F(0,-2);
综上,点的坐标为或或.
18、(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
∴点B的横坐标是2m.
又∵点B在双曲线y= (x>0)上,
∴B(2m,).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m, ),B(2m, ),
∴P(m, ),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为 BP AP=3,
∴BP AP=1,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A. B都在双曲线y= (x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OC AC=BP 2AP=12.
∴该双曲线的解析式是:y= .
一、填空题(本大题共5个小题,每小题4分,共20分)
19、1
20、1
21、
22、1
23、1
二、解答题(本大题共3个小题,共30分)
24、(1)由图象可得:甲公司每小时的租费是15元;
故答案为:15;
(2)设y1=k1x+80,
把点(1,95)代入,可得
95=k1+80,
解得k1=15,
∴y1=15x+80(x≥0);
设y2=k2x,
把(1,30)代入,可得
30=k2,即k2=30,
∴y2=30x(x≥0);
(3)当y1=y2时,15x+80=30x,
解得x=;
当y1>y2时,15x+80>30x,
解得x<;
当y1<y2时,15x+80<30x,
解得x>;
∴当租车时间为小时,选择甲乙公司一样合算;当租车时间小于小时,选择乙公司合算;当租车时间大于小时,选择甲公司合算.
25、解:(1)根据题意,可得点
将其代入反比例函数解析式,即得
(2)根据题意,得
解得
∴点B(4,-2)
∴直接观察图像,可得的解集为
或
(3)过点作轴,过点作轴,交于点
根据题意,可得
∴∠EAB=∠NOB=∠OCD,∠AEB=∠COD=90°,AB=CD
∴∠ABE=∠CDO
∴(ASA)
∴
则可得出直线CD为
此题主要考查一次函数、反比例函数和平行四边形的综合应用,熟练运用,即可解题.
26、 (1)连接BD,作BD的垂直平分线交AD、BC与E、F,连接BE,DF即可,如图,菱形即为所求.
(2)设的长为,
∵,
∴,
∴在中,,
即,
解得,即菱形的边长为.
第12页,共13页
同课章节目录
