2.3一元一次方程(第2课时) 课件(共20张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 2.3一元一次方程(第2课时) 课件(共20张PPT) 2024-2025学年数学北师版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 00:48:32 | ||
图片预览


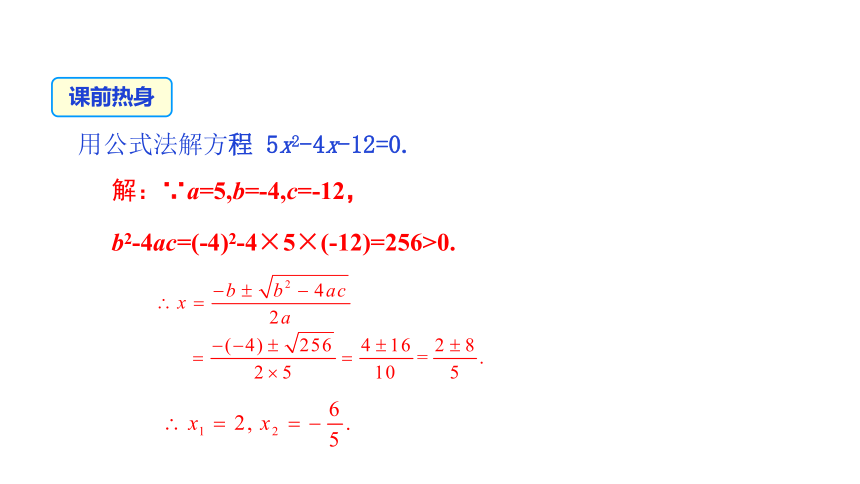



文档简介
(共20张PPT)
2.3用公式法求解一元二次方程
(第2课时 利用一元二次方程解决面积问题)
第二章 一元二次方程
C
B
D
A
公式法解方程的步骤
1.变形: 化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数;
3.计算: b2-4ac的值;
4.判断:若b2-4ac ≥0,则利用求根公式求出;
若b2-4ac<0,则方程没有实数根.
课前热身
用公式法解方程 5x2-4x-12=0.
解:∵a=5,b=-4,c=-12,
b2-4ac=(-4)2-4×5×(-12)=256>0.
本节学习目标
1.掌握面积法建立一元二次方程的数学模型.(难点)
2.能运用一元二次方程解决与面积有关的实际问题.(重点)
问题引入
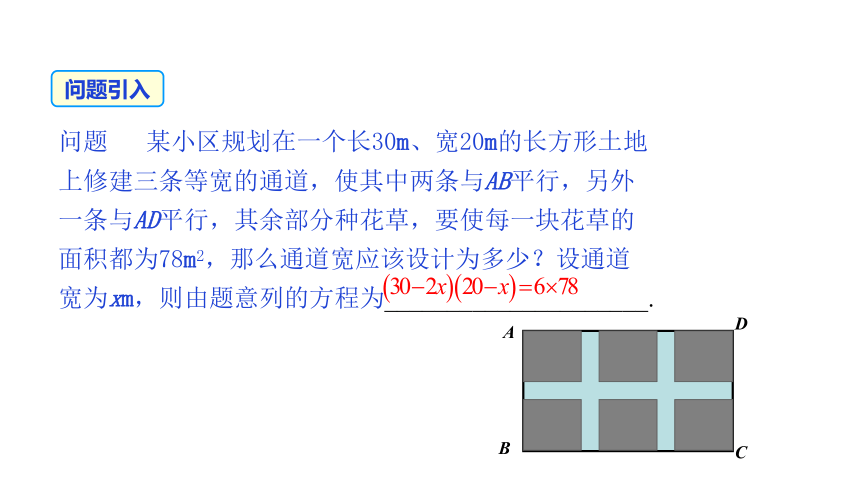
问题 某小区规划在一个长30m、宽20m的长方形土地上修建三条等宽的通道,使其中两条与AB平行,另外一条与AD平行,其余部分种花草,要使每一块花草的面积都为78m2,那么通道宽应该设计为多少?设通道宽为xm,则由题意列的方程为_____________________.
C
B
D
A
利用一元二次方程解决面积问题
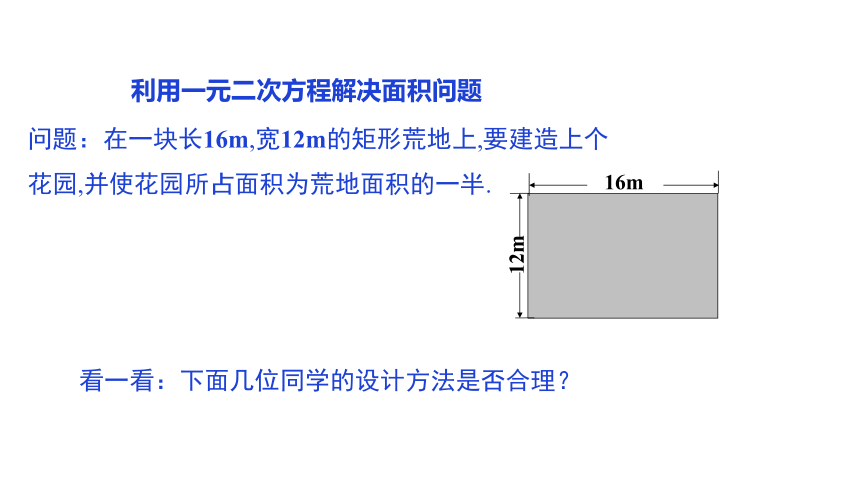
问题:在一块长16m,宽12m的矩形荒地上,要建造上个
花园,并使花园所占面积为荒地面积的一半.
16m
12m
看一看:下面几位同学的设计方法是否合理?
小明设计:
如右图所示.其中花园四周小路的宽都相等.通过解方程, 得到小路的宽为2m或12m.
问题:他的结果对吗?你能将小明的解答过程重现吗?
解:设小路的宽为 xm, 根据题意得:
即 x2 - 14x + 24 = 0.
解方程得 x1 = 2 , x2 = 12.
将x =12 代入方程中不符合题意舍去.
答:小路的宽为2m.
16m
12m
x
x
解:设扇形半径为 xm, 根据题意得:
即 πx2 = 96.
解方程得 x1 = , x2 = (舍去),
答:扇形半径约为5.5m.
小亮设计:如右图所示.其中花园每个角上的
扇形都相同.
16m
12m
问题:你能帮小亮计算一下这个扇形的半径
是多少吗?
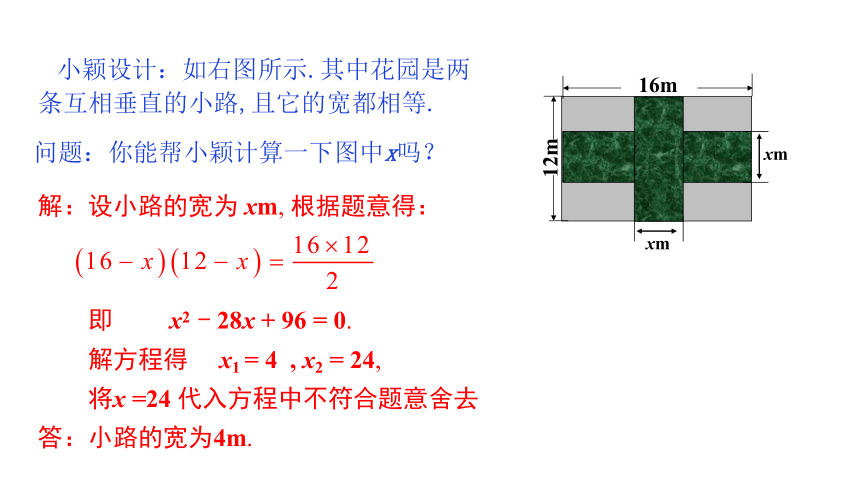
小颖设计:如右图所示.其中花园是两条互相垂直的小路,且它的宽都相等.
16m
12m
xm
xm
问题:你能帮小颖计算一下图中x吗?
解:设小路的宽为 xm, 根据题意得:
即 x2 - 28x + 96 = 0.
解方程得 x1 = 4 , x2 = 24,
将x =24 代入方程中不符合题意舍去
答:小路的宽为4m.
典例精析
例1:要设计一本书的封面,封面长27㎝,宽21cm正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何
设计四周边衬的宽度?(精确到0.1cm)
27cm
21cm
分析:这本书的长宽之比 : 正中央的矩形
长宽之比 : ,上下边衬与左右边衬之
比 : .
9 7
9 7
9 7
27cm
21cm
解:设中央长方形的长和宽分别为9a和7a由此得到上下边衬宽度之比为:
解:设上下边衬为9xcm,左右边衬宽为7xcm依
题意得
解方程得
故上下边衬的宽度为:
故左右边衬的宽度为:
方程的哪个根合乎实际意义
为什么
试一试:如果换一种设未知数的方法,是否可以更简单地解决上面的问题?
27cm
21cm
解:设正中央的矩形两边别为9xcm,7xcm.依题意得
解得
故上下边衬的宽度为:
故左右边衬的宽度为:
例2:如图所示,在△ABC中,∠C=90°, AC=6cm,BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动;同时点Q沿CB边从点C向终点B以2cm/s的速度移动,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后可使△PCQ的面积为9 cm ?
解:若设出发x s后可使△PCQ的面积为9cm
根据题意得AP= xcm,PC=(6-x)cm,CQ=2xcm
整理,得
解得 x1= x2=3
答:点P,Q出发3s后可使△PCQ的面积为9cm .
方法点拨
主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程;
例4:如图:要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB和BC的长分别是多少米?
解:设AB长是x m.
(100-4x)x=400.
x2-25x+100=0.
x1=5,x2=20.
x=20,100-4x=20<25.
x=5,100-4x=80>25, x=5(舍去).
答:羊圈的边长AB和BC的长分别是20m,20m.
D
C
B
A
25米
几何图形与一元二次方程问题
几何图形
常见几何图形面积是等量关系.
类 型
课本封面问题
彩条/小路宽度问题
常采用图形平移,聚零为整,方便列方程
(2020 徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,
宽为(20﹣2x)cm,高为xcm,
当x=10时,20﹣2x=0,不合题意,舍去
根据题意:2×[(30﹣2x)+(20﹣2x)]x=200
(2020 巴彦淖尔)如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
解:设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m,
由已知得:(30﹣3x) (24﹣2x)=480,
解得:x1=2,x2=20,
当x=20时,30﹣3x=﹣30,24﹣2x=﹣16,
不符合题意,
意志坚强的人能把世界放在手中像泥块一样任意揉捏。
-------- 歌德
2.3用公式法求解一元二次方程
(第2课时 利用一元二次方程解决面积问题)
第二章 一元二次方程
C
B
D
A
公式法解方程的步骤
1.变形: 化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数;
3.计算: b2-4ac的值;
4.判断:若b2-4ac ≥0,则利用求根公式求出;
若b2-4ac<0,则方程没有实数根.
课前热身
用公式法解方程 5x2-4x-12=0.
解:∵a=5,b=-4,c=-12,
b2-4ac=(-4)2-4×5×(-12)=256>0.
本节学习目标
1.掌握面积法建立一元二次方程的数学模型.(难点)
2.能运用一元二次方程解决与面积有关的实际问题.(重点)
问题引入
问题 某小区规划在一个长30m、宽20m的长方形土地上修建三条等宽的通道,使其中两条与AB平行,另外一条与AD平行,其余部分种花草,要使每一块花草的面积都为78m2,那么通道宽应该设计为多少?设通道宽为xm,则由题意列的方程为_____________________.
C
B
D
A
利用一元二次方程解决面积问题
问题:在一块长16m,宽12m的矩形荒地上,要建造上个
花园,并使花园所占面积为荒地面积的一半.
16m
12m
看一看:下面几位同学的设计方法是否合理?
小明设计:
如右图所示.其中花园四周小路的宽都相等.通过解方程, 得到小路的宽为2m或12m.
问题:他的结果对吗?你能将小明的解答过程重现吗?
解:设小路的宽为 xm, 根据题意得:
即 x2 - 14x + 24 = 0.
解方程得 x1 = 2 , x2 = 12.
将x =12 代入方程中不符合题意舍去.
答:小路的宽为2m.
16m
12m
x
x
解:设扇形半径为 xm, 根据题意得:
即 πx2 = 96.
解方程得 x1 = , x2 = (舍去),
答:扇形半径约为5.5m.
小亮设计:如右图所示.其中花园每个角上的
扇形都相同.
16m
12m
问题:你能帮小亮计算一下这个扇形的半径
是多少吗?
小颖设计:如右图所示.其中花园是两条互相垂直的小路,且它的宽都相等.
16m
12m
xm
xm
问题:你能帮小颖计算一下图中x吗?
解:设小路的宽为 xm, 根据题意得:
即 x2 - 28x + 96 = 0.
解方程得 x1 = 4 , x2 = 24,
将x =24 代入方程中不符合题意舍去
答:小路的宽为4m.
典例精析
例1:要设计一本书的封面,封面长27㎝,宽21cm正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何
设计四周边衬的宽度?(精确到0.1cm)
27cm
21cm
分析:这本书的长宽之比 : 正中央的矩形
长宽之比 : ,上下边衬与左右边衬之
比 : .
9 7
9 7
9 7
27cm
21cm
解:设中央长方形的长和宽分别为9a和7a由此得到上下边衬宽度之比为:
解:设上下边衬为9xcm,左右边衬宽为7xcm依
题意得
解方程得
故上下边衬的宽度为:
故左右边衬的宽度为:
方程的哪个根合乎实际意义
为什么
试一试:如果换一种设未知数的方法,是否可以更简单地解决上面的问题?
27cm
21cm
解:设正中央的矩形两边别为9xcm,7xcm.依题意得
解得
故上下边衬的宽度为:
故左右边衬的宽度为:
例2:如图所示,在△ABC中,∠C=90°, AC=6cm,BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动;同时点Q沿CB边从点C向终点B以2cm/s的速度移动,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后可使△PCQ的面积为9 cm ?
解:若设出发x s后可使△PCQ的面积为9cm
根据题意得AP= xcm,PC=(6-x)cm,CQ=2xcm
整理,得
解得 x1= x2=3
答:点P,Q出发3s后可使△PCQ的面积为9cm .
方法点拨
主要集中在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程;
例4:如图:要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB和BC的长分别是多少米?
解:设AB长是x m.
(100-4x)x=400.
x2-25x+100=0.
x1=5,x2=20.
x=20,100-4x=20<25.
x=5,100-4x=80>25, x=5(舍去).
答:羊圈的边长AB和BC的长分别是20m,20m.
D
C
B
A
25米
几何图形与一元二次方程问题
几何图形
常见几何图形面积是等量关系.
类 型
课本封面问题
彩条/小路宽度问题
常采用图形平移,聚零为整,方便列方程
(2020 徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,
宽为(20﹣2x)cm,高为xcm,
当x=10时,20﹣2x=0,不合题意,舍去
根据题意:2×[(30﹣2x)+(20﹣2x)]x=200
(2020 巴彦淖尔)如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
解:设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m,
由已知得:(30﹣3x) (24﹣2x)=480,
解得:x1=2,x2=20,
当x=20时,30﹣3x=﹣30,24﹣2x=﹣16,
不符合题意,
意志坚强的人能把世界放在手中像泥块一样任意揉捏。
-------- 歌德
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
