2.2.2用配方法求解一元二次方程(第2课时) 课件(共20张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 2.2.2用配方法求解一元二次方程(第2课时) 课件(共20张PPT) 2024-2025学年数学北师版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 00:49:50 | ||
图片预览







文档简介
(共20张PPT)
(第2课时)
2.2 用配方法求解一元二次方程
第二章一元二次方程
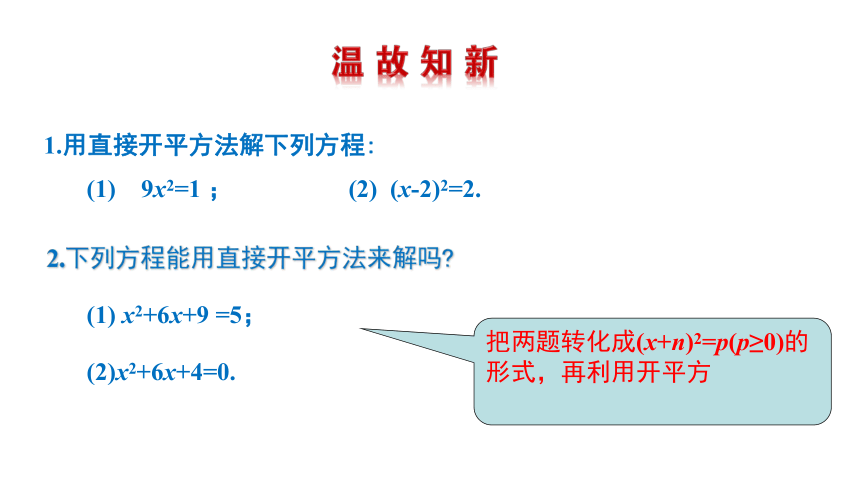
(1) 9x2=1 ;
(2) (x-2)2=2.
2.下列方程能用直接开平方法来解吗
1.用直接开平方法解下列方程:
(1) x2+6x+9 =5;
(2)x2+6x+4=0.
把两题转化成(x+n)2=p(p≥0)的
形式,再利用开平方
1.会用配方法解二次项系数不为1的一元二次方程;(重点)
2.能够熟练地、灵活地应用配方法解一元二次方程.(难点)
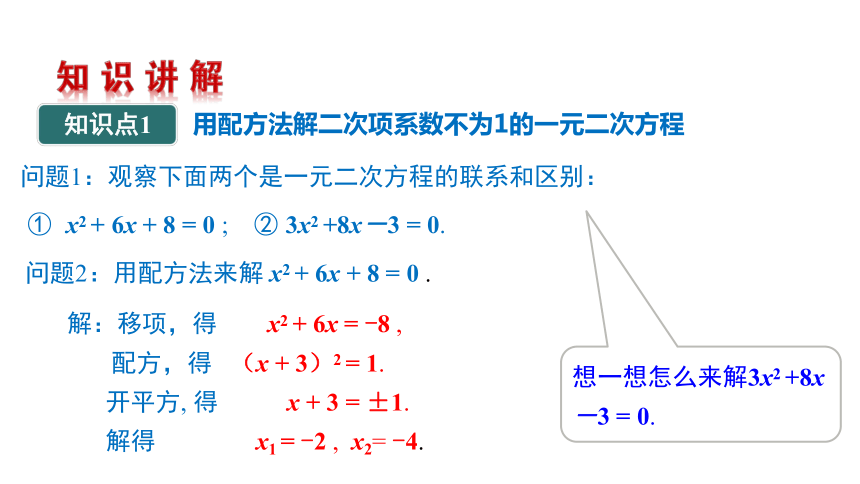
问题1:观察下面两个是一元二次方程的联系和区别:
① x2 + 6x + 8 = 0 ; ② 3x2 +8x-3 = 0.
问题2:用配方法来解 x2 + 6x + 8 = 0 .
解:移项,得 x2 + 6x = -8 ,
配方,得 (x + 3)2 = 1.
开平方, 得 x + 3 = ±1.
解得 x1 = -2 , x2= -4.
想一想怎么来解3x2 +8x-3 = 0.
用配方法解二次项系数不为1的一元二次方程
知识点1
所以x1= , x2 = -3 .
②解方程: 3x2 + 8x -3 = 0.
解:
即x + = 或 x + = .
移项得x + =± ,
配方得 x2 + x + ( ) 2 - ( )2 - 1 = 0,
(x + )2 - =0.
两边同除以3,得x2 + x - 1=0.
配方,得
由此可得
二次项系数化为1,得
解:移项,得
2x2-3x=-1,
即
移项和二次项系数化为1这两个步骤能不能交换一下呢
例1 解下列方程:
配方,得
因为实数的平方不会是负数,所以x取任何实数时,上式都不成立,所以原方程无实数根.
解:移项,得
二次项系数化为1,得
为什么方程两边都加12?
即
思考1:用配方法解一元二次方程时,移项时要
注意些什么?
思考2:用配方法解一元二次方程的一般步骤.
移项时需注意改变符号.
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p.
①当p>0时,则 x+n = , 方程的两个根为
规律总结
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为
x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
例1.一个小球从地面上以15m/s的初速度竖直向上弹出,它在空中的高度h (m)与时间 t (s)满足关系:
h=15t - 5t2.
小球何时能达到10m高?
解:将 h = 10代入方程式中.
15t - 5t2 = 10.
两边同时除以-5,得 t2 - 3t = -2,
配方,得 t2 - 3t + ( )2= ( )2 - 2,
(t - )2 =
配方法的应用
知识点2
移项,得 (t - )2 =
即 t - = ,或 t - = .
所以 t1= 2 , t2 = 1 .
①二次项系数要化为1;②在二次项系数化为1时,常数项也要除以二次项系数;③配方时,两边同时加上一次项系数一半的平方.
注意
即在1s或2s时,小球可达10m高.
例2.试用配方法说明:不论k取何实数,多项式
k2-4k+5 的值必定大于零.
解:k2-4k+5=k2-4k+4+1
=(k-2)2+1
因为(k-2)2≥0,所以(k-2)2+1≥1.
所以k2-4k+5的值必定大于零.
例3.用配方法解方 程 x2 + x = 0.
解:方程两边同时除以 ,得
x2 - 5x + = 0 .
移项,得 x2 - 5x = - ,
配方, 得 x2 - 5x + ( )2= ( )2 - .
即 (x + )2 = .
两边开平方,得 x - = ±
即 x - = 或 x - =
所以 x1 = x2 =
配方法的应用
类别 解题策略
1.求最值或
证明代数式
的值为恒正
(或负)
对于一个关于x的二次多项式通过配方成a(x+m)2
+n的形式后,(x+m)2≥0,n为常数,当a>0时,可知其最小值;当a<0时,可知其最大值.
2.完全平方式中的配方
如:已知x2-2mx+16是一个完全平方式,所以一次项系数一半的平方等于16,即m2=16,m=±4.
3.利用配方构成非负数和的形式
对于含有多个未知数的二次式的等式,求未知数的值,解题突破口往往是配方成多个完全平方式得其和为0,再根据非负数的和为0,各项均为0,从而求解.如:a2+b2-4b+4=0,则a2+(b-2)2=0,即a=0,b=2.
配方法
方法
步骤
一移常数项;
二配方[配上 ];
三写成(x+n)2=p (p ≥0);
四直接开平方法解方程.
特别提醒:
在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
应用
求代数式的最值或证明
在方程两边都配上
1.(2021 南岗质检)用配方法解一元二次方程x2-4x+1=0,配方
正确的是( )
A.(x-1)2=12
B.(x-2)2=3
C.(x-1)2=0
D.(x-2)2=4
B
2.(2021 鼓楼质检)用配方法解一元二次方程2x2-4x-1=0,配方正
确的是( )
3
2
A.(x-1)2=
B.(x-1)2=2
3
2
C.(x-2)2=
D.(x-2)2=2
A
3.(2021 覃塘期末)用配方法解一元二次方程x2+6x-5=0时,配
方后得到的方程为( )
A.(x+3)2=9
B.(x+3)2=14
D.(x-5)2=6
C.(x+6)2=41
B
4.嘉琪准备完成题目:解一元二次方程x2-6x+□=0. (1)若“□”表示常数-7,请你用配方法解方程:x2-6x-7=0; (2)若“□”表示一个字母,且一元二次方程x2-6x+□=0有实数根.求“□”的最大值.
解:(1)x2-6x-7=0,
x2-6x+32=7+32,即(x-3)2=16,
解得x1=7,x2=-1.
(2)设□中为m,则x2-6x+m=0,
由题意得,△=b2-4ac=(-6)2-4×1×m≥0,
解得m≤9,
∴□的最大的值为9.
人生不是受环境的支配,而是受自己习惯思想的恐吓.
——赫胥黎
(第2课时)
2.2 用配方法求解一元二次方程
第二章一元二次方程
(1) 9x2=1 ;
(2) (x-2)2=2.
2.下列方程能用直接开平方法来解吗
1.用直接开平方法解下列方程:
(1) x2+6x+9 =5;
(2)x2+6x+4=0.
把两题转化成(x+n)2=p(p≥0)的
形式,再利用开平方
1.会用配方法解二次项系数不为1的一元二次方程;(重点)
2.能够熟练地、灵活地应用配方法解一元二次方程.(难点)
问题1:观察下面两个是一元二次方程的联系和区别:
① x2 + 6x + 8 = 0 ; ② 3x2 +8x-3 = 0.
问题2:用配方法来解 x2 + 6x + 8 = 0 .
解:移项,得 x2 + 6x = -8 ,
配方,得 (x + 3)2 = 1.
开平方, 得 x + 3 = ±1.
解得 x1 = -2 , x2= -4.
想一想怎么来解3x2 +8x-3 = 0.
用配方法解二次项系数不为1的一元二次方程
知识点1
所以x1= , x2 = -3 .
②解方程: 3x2 + 8x -3 = 0.
解:
即x + = 或 x + = .
移项得x + =± ,
配方得 x2 + x + ( ) 2 - ( )2 - 1 = 0,
(x + )2 - =0.
两边同除以3,得x2 + x - 1=0.
配方,得
由此可得
二次项系数化为1,得
解:移项,得
2x2-3x=-1,
即
移项和二次项系数化为1这两个步骤能不能交换一下呢
例1 解下列方程:
配方,得
因为实数的平方不会是负数,所以x取任何实数时,上式都不成立,所以原方程无实数根.
解:移项,得
二次项系数化为1,得
为什么方程两边都加12?
即
思考1:用配方法解一元二次方程时,移项时要
注意些什么?
思考2:用配方法解一元二次方程的一般步骤.
移项时需注意改变符号.
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成
(x+n)2=p.
①当p>0时,则 x+n = , 方程的两个根为
规律总结
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为
x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
例1.一个小球从地面上以15m/s的初速度竖直向上弹出,它在空中的高度h (m)与时间 t (s)满足关系:
h=15t - 5t2.
小球何时能达到10m高?
解:将 h = 10代入方程式中.
15t - 5t2 = 10.
两边同时除以-5,得 t2 - 3t = -2,
配方,得 t2 - 3t + ( )2= ( )2 - 2,
(t - )2 =
配方法的应用
知识点2
移项,得 (t - )2 =
即 t - = ,或 t - = .
所以 t1= 2 , t2 = 1 .
①二次项系数要化为1;②在二次项系数化为1时,常数项也要除以二次项系数;③配方时,两边同时加上一次项系数一半的平方.
注意
即在1s或2s时,小球可达10m高.
例2.试用配方法说明:不论k取何实数,多项式
k2-4k+5 的值必定大于零.
解:k2-4k+5=k2-4k+4+1
=(k-2)2+1
因为(k-2)2≥0,所以(k-2)2+1≥1.
所以k2-4k+5的值必定大于零.
例3.用配方法解方 程 x2 + x = 0.
解:方程两边同时除以 ,得
x2 - 5x + = 0 .
移项,得 x2 - 5x = - ,
配方, 得 x2 - 5x + ( )2= ( )2 - .
即 (x + )2 = .
两边开平方,得 x - = ±
即 x - = 或 x - =
所以 x1 = x2 =
配方法的应用
类别 解题策略
1.求最值或
证明代数式
的值为恒正
(或负)
对于一个关于x的二次多项式通过配方成a(x+m)2
+n的形式后,(x+m)2≥0,n为常数,当a>0时,可知其最小值;当a<0时,可知其最大值.
2.完全平方式中的配方
如:已知x2-2mx+16是一个完全平方式,所以一次项系数一半的平方等于16,即m2=16,m=±4.
3.利用配方构成非负数和的形式
对于含有多个未知数的二次式的等式,求未知数的值,解题突破口往往是配方成多个完全平方式得其和为0,再根据非负数的和为0,各项均为0,从而求解.如:a2+b2-4b+4=0,则a2+(b-2)2=0,即a=0,b=2.
配方法
方法
步骤
一移常数项;
二配方[配上 ];
三写成(x+n)2=p (p ≥0);
四直接开平方法解方程.
特别提醒:
在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
应用
求代数式的最值或证明
在方程两边都配上
1.(2021 南岗质检)用配方法解一元二次方程x2-4x+1=0,配方
正确的是( )
A.(x-1)2=12
B.(x-2)2=3
C.(x-1)2=0
D.(x-2)2=4
B
2.(2021 鼓楼质检)用配方法解一元二次方程2x2-4x-1=0,配方正
确的是( )
3
2
A.(x-1)2=
B.(x-1)2=2
3
2
C.(x-2)2=
D.(x-2)2=2
A
3.(2021 覃塘期末)用配方法解一元二次方程x2+6x-5=0时,配
方后得到的方程为( )
A.(x+3)2=9
B.(x+3)2=14
D.(x-5)2=6
C.(x+6)2=41
B
4.嘉琪准备完成题目:解一元二次方程x2-6x+□=0. (1)若“□”表示常数-7,请你用配方法解方程:x2-6x-7=0; (2)若“□”表示一个字母,且一元二次方程x2-6x+□=0有实数根.求“□”的最大值.
解:(1)x2-6x-7=0,
x2-6x+32=7+32,即(x-3)2=16,
解得x1=7,x2=-1.
(2)设□中为m,则x2-6x+m=0,
由题意得,△=b2-4ac=(-6)2-4×1×m≥0,
解得m≤9,
∴□的最大的值为9.
人生不是受环境的支配,而是受自己习惯思想的恐吓.
——赫胥黎
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
