3.1用树状图或表格求概率(第2课时) 课件(共25张PPT) 2024-2025学年数学北师大版九年级上册
文档属性
| 名称 | 3.1用树状图或表格求概率(第2课时) 课件(共25张PPT) 2024-2025学年数学北师大版九年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 984.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-21 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第2课时
3.1 用树状图或表格求概率
第三章 概率的进一步认识
用画树状图和列表的方法求概率时应注意各种结果出现的可能性相同.
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,较方便地求出某些事件发生的概率.
借助于树状图、列表法计算随机事件的概率.
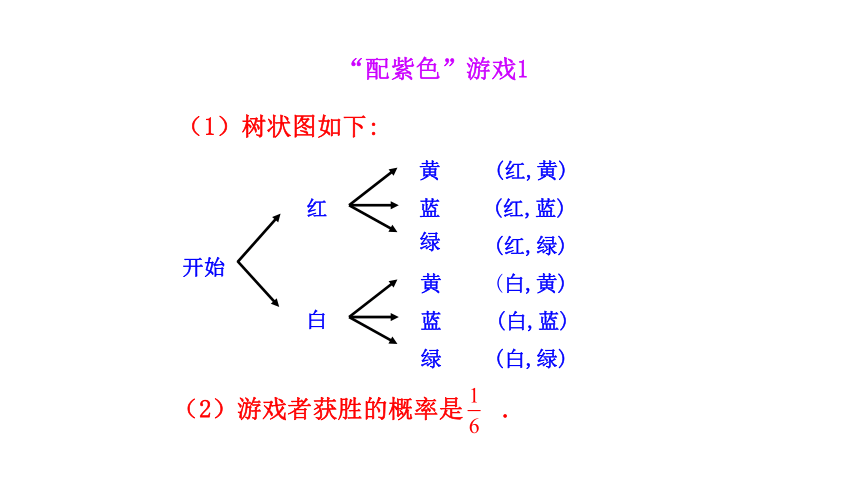
小颖为学校联欢会设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用画树状图或列表的方法
表示游戏所有可能出现的结果.
(2)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
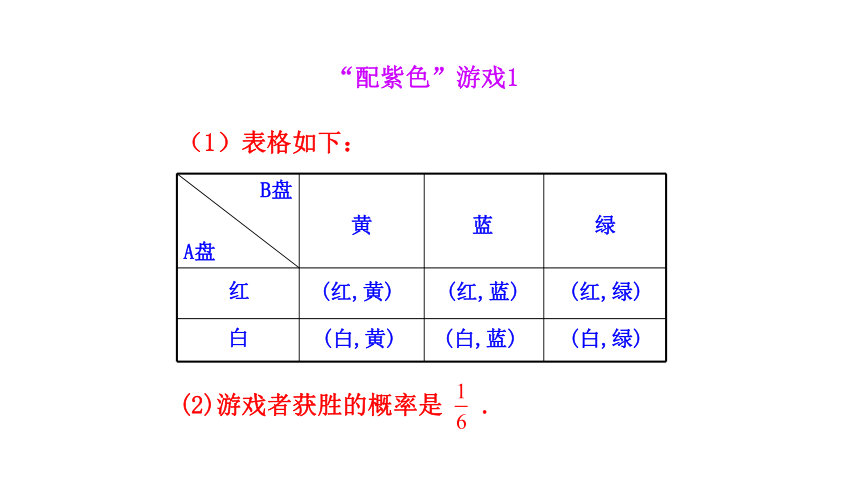
(1)树状图如下:
“配紫色”游戏1
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
(2)游戏者获胜的概率是 .
(1)表格如下:
“配紫色”游戏1
(2)游戏者获胜的概率是 .
B盘
A盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
120°
红
红
蓝
蓝
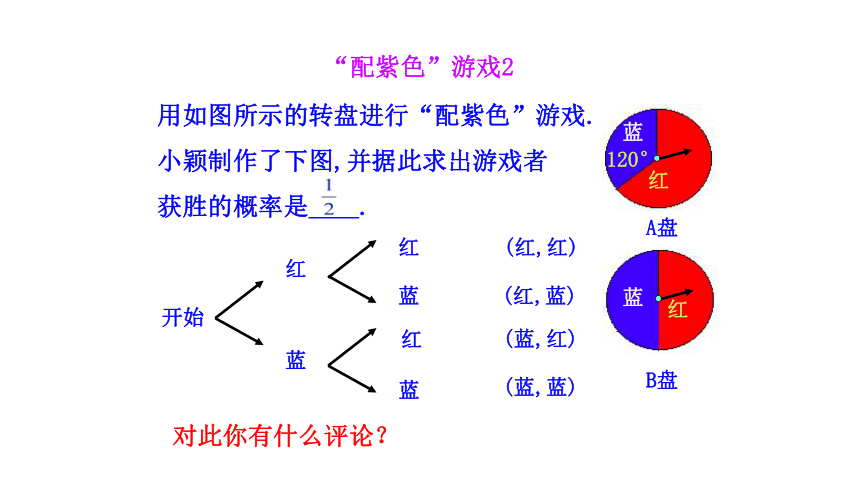
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者
获胜的概率是 .
“配紫色”游戏2
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
A盘
B盘
小亮则先把A盘的红色区域等分成2份,分
别记作“红1”,“红2”,然后制作了下表,
据此求出游戏者获胜的概率也是 .
120°
红1
红
蓝
蓝
红2
你认为谁做得对 说说你的理由.
B盘
A盘 红 蓝
红1 (红1,红) (红1,蓝)
红2 (红2,红) (红2,蓝)
蓝 (蓝,红) (蓝,蓝)
“配紫色”游戏3
A盘
B盘
小颖的做法不正确.因为A盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法正确,他的方法是解决这类问题的一种常用方法.
【结论】
1
2
3
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并且自由转动图中的转盘(转盘被分成面积相等的三个扇形).
游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
【例1】
【解析】每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有1种:(1,1),因此游戏者获胜的概率为 .
转盘
摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
你能用树状图解答吗?试试看!
桌面上有5张背面相同的卡片,正面分别写着数字“1”、“2”、“3”、“4”、“5”.将卡片背面朝上洗匀.
(1)小军从中任意抽取一张,抽到偶数的概率是 ;
(2)小红从中同时抽取两张.规定:抽到的两张卡片上的数字之和为奇数,则小军胜,否则小红胜.你认为这个游戏公平吗?请用树状图或表格说明你的理由.
【例2】
概率与游戏
的综合应用
配紫色
判断游戏公平性
红色+蓝色=紫色
判断游戏参与者获
胜的概率是否相同
1.(2021 武昌模拟)一个不透明的口袋中有四个完全相
同的小球,把它们分别标号为1,2,3,4.若一次性摸
出两个球,则一次性取出的两个小球标号的和不小于4
的概率是( )
D
2.(2021 广西模拟)消费者在网店购物后,将从“好评、中
评、差评”中选择一种作为对卖家的评价,假设这三种评价是
等可能的,若小明、小亮在某网店购买了同一商品,且都给出
了评价,则两人中至少有一个给“好评”的概率为( ).
C
3.为了防控输入性“新冠肺炎”,某医院成立隔离治疗发
热病人防控小组,决定从内科3位骨干医师中(含有
甲)抽调2人组成.则甲一定会被抽调到防控小组的概
率是( )
C
4.(2021 洛阳模拟)小明在概率活动课上制作了四张卡
片,卡片正面分别标有数字2,4, (卡片除所标数字
外,其他均相同),并将其背面朝上放置.现从中随机抽
出两张卡片,则两张卡片上的数字均为有理数的概率
为 .
5.(2021 兰州模拟)转动如图所示的两个转盘(每个转
盘被分成五个面积相等的扇形)各一次,两次转得的数字
之和大于7的概率是 .
6.(2021 温江模拟)今年某市体育中考将于4月上旬开展.为备战体考,某校初三年级学生利用每天大课时间对坐位体前屈、立定跳远和长跑三项运动进行专项训练.为了解同学们对这三项运动训练技巧的掌握情况,随机抽取了若干名学生进行调查,并将调查结果分成了四类:掌握3项技巧的为A类,掌握2项技巧的为B类,掌握1项技巧的为C类,掌握0项技巧的为D类,并绘制成两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)本次被调查的学生共有 人,请补全条形统计图;
(2)若该校初三年级共有1500名学生,请估计该校初三年级大约有多少名学生掌握了3项训练项目技巧;
(3)D类的4名同学中有且仅有2名来自同一个班,现从D类的4名同学中随机抽取2名同学进行强化训练,请用树状图或表格法求抽到的两个人恰好来自同一个班的概率.
解:(1)16÷40%=40(人),
则C类的人数为:40﹣8﹣16﹣4=12(人),
答案:40
补全条形统计图:
(3)来自同一个班的同学记为A,其他2名同学
记为B,C,
画树状图如图:
人的生命,似洪水奔流,不遇着岛屿和暗礁,难以击起美丽的浪花.
——佚名
第2课时
3.1 用树状图或表格求概率
第三章 概率的进一步认识
用画树状图和列表的方法求概率时应注意各种结果出现的可能性相同.
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,较方便地求出某些事件发生的概率.
借助于树状图、列表法计算随机事件的概率.
小颖为学校联欢会设计了一个“配紫色”的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用画树状图或列表的方法
表示游戏所有可能出现的结果.
(2)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
(1)树状图如下:
“配紫色”游戏1
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
(2)游戏者获胜的概率是 .
(1)表格如下:
“配紫色”游戏1
(2)游戏者获胜的概率是 .
B盘
A盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
120°
红
红
蓝
蓝
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者
获胜的概率是 .
“配紫色”游戏2
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
A盘
B盘
小亮则先把A盘的红色区域等分成2份,分
别记作“红1”,“红2”,然后制作了下表,
据此求出游戏者获胜的概率也是 .
120°
红1
红
蓝
蓝
红2
你认为谁做得对 说说你的理由.
B盘
A盘 红 蓝
红1 (红1,红) (红1,蓝)
红2 (红2,红) (红2,蓝)
蓝 (蓝,红) (蓝,蓝)
“配紫色”游戏3
A盘
B盘
小颖的做法不正确.因为A盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法正确,他的方法是解决这类问题的一种常用方法.
【结论】
1
2
3
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并且自由转动图中的转盘(转盘被分成面积相等的三个扇形).
游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
【例1】
【解析】每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有1种:(1,1),因此游戏者获胜的概率为 .
转盘
摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
你能用树状图解答吗?试试看!
桌面上有5张背面相同的卡片,正面分别写着数字“1”、“2”、“3”、“4”、“5”.将卡片背面朝上洗匀.
(1)小军从中任意抽取一张,抽到偶数的概率是 ;
(2)小红从中同时抽取两张.规定:抽到的两张卡片上的数字之和为奇数,则小军胜,否则小红胜.你认为这个游戏公平吗?请用树状图或表格说明你的理由.
【例2】
概率与游戏
的综合应用
配紫色
判断游戏公平性
红色+蓝色=紫色
判断游戏参与者获
胜的概率是否相同
1.(2021 武昌模拟)一个不透明的口袋中有四个完全相
同的小球,把它们分别标号为1,2,3,4.若一次性摸
出两个球,则一次性取出的两个小球标号的和不小于4
的概率是( )
D
2.(2021 广西模拟)消费者在网店购物后,将从“好评、中
评、差评”中选择一种作为对卖家的评价,假设这三种评价是
等可能的,若小明、小亮在某网店购买了同一商品,且都给出
了评价,则两人中至少有一个给“好评”的概率为( ).
C
3.为了防控输入性“新冠肺炎”,某医院成立隔离治疗发
热病人防控小组,决定从内科3位骨干医师中(含有
甲)抽调2人组成.则甲一定会被抽调到防控小组的概
率是( )
C
4.(2021 洛阳模拟)小明在概率活动课上制作了四张卡
片,卡片正面分别标有数字2,4, (卡片除所标数字
外,其他均相同),并将其背面朝上放置.现从中随机抽
出两张卡片,则两张卡片上的数字均为有理数的概率
为 .
5.(2021 兰州模拟)转动如图所示的两个转盘(每个转
盘被分成五个面积相等的扇形)各一次,两次转得的数字
之和大于7的概率是 .
6.(2021 温江模拟)今年某市体育中考将于4月上旬开展.为备战体考,某校初三年级学生利用每天大课时间对坐位体前屈、立定跳远和长跑三项运动进行专项训练.为了解同学们对这三项运动训练技巧的掌握情况,随机抽取了若干名学生进行调查,并将调查结果分成了四类:掌握3项技巧的为A类,掌握2项技巧的为B类,掌握1项技巧的为C类,掌握0项技巧的为D类,并绘制成两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)本次被调查的学生共有 人,请补全条形统计图;
(2)若该校初三年级共有1500名学生,请估计该校初三年级大约有多少名学生掌握了3项训练项目技巧;
(3)D类的4名同学中有且仅有2名来自同一个班,现从D类的4名同学中随机抽取2名同学进行强化训练,请用树状图或表格法求抽到的两个人恰好来自同一个班的概率.
解:(1)16÷40%=40(人),
则C类的人数为:40﹣8﹣16﹣4=12(人),
答案:40
补全条形统计图:
(3)来自同一个班的同学记为A,其他2名同学
记为B,C,
画树状图如图:
人的生命,似洪水奔流,不遇着岛屿和暗礁,难以击起美丽的浪花.
——佚名
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
