4.3 相似多边形 课件(共23张PPT)2024-2025学年数学北师大版九年级上册
文档属性
| 名称 | 4.3 相似多边形 课件(共23张PPT)2024-2025学年数学北师大版九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 780.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-21 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
4.3 相似多边形
第四章 图形的相似
问题:用同一张底片洗出不同尺寸的照片,两张图片相似吗
情境导入
1.经历相似多边形概念的形成过程,了解相似多
边形的含义.
2.在探索相似多边形的边、角关系中,进一步发
展学生的观察、判断、归纳能力.
3.在交流和反思过程中,体验数学活动中充满了
探索性和创造性.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
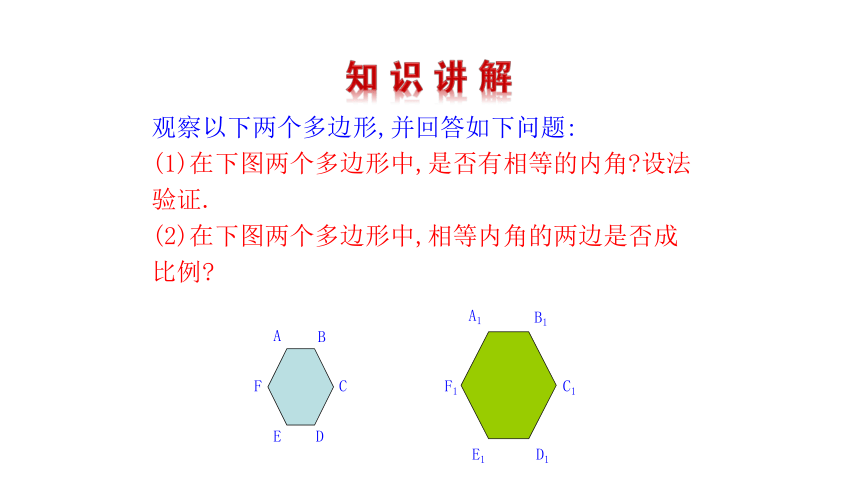
观察以下两个多边形,并回答如下问题:
(1)在下图两个多边形中,是否有相等的内角 设法验证.
(2)在下图两个多边形中,相等内角的两边是否成比例
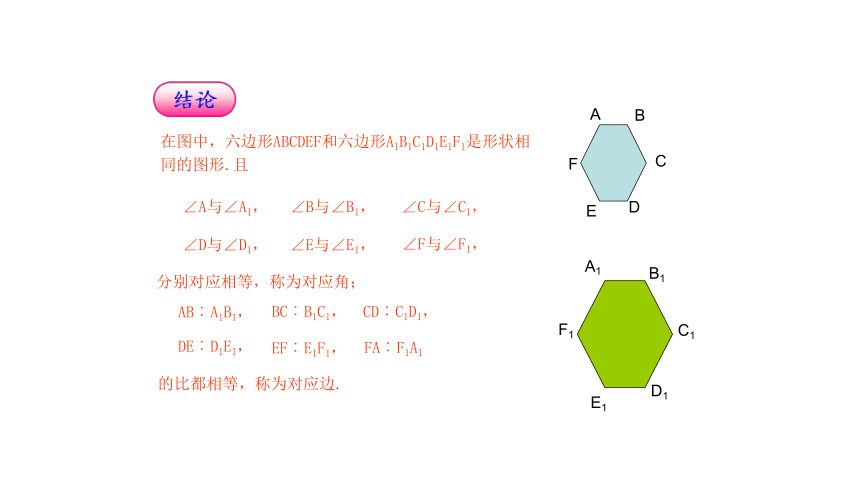
在图中,六边形ABCDEF和六边形A1B1C1D1E1F1是形状相同的图形.且
∠A与∠A1,
∠B与∠B1,
∠C与∠C1,
∠D与∠D1,
∠E与∠E1,
∠F与∠F1,
分别对应相等,称为对应角;
AB︰A1B1,
BC︰B1C1,
CD︰C1D1,
DE︰D1E1,
EF︰E1F1,
FA︰F1A1
的比都相等,称为对应边.
A
B
D
E
F
A1
B1
D1
E1
F1
C1
C
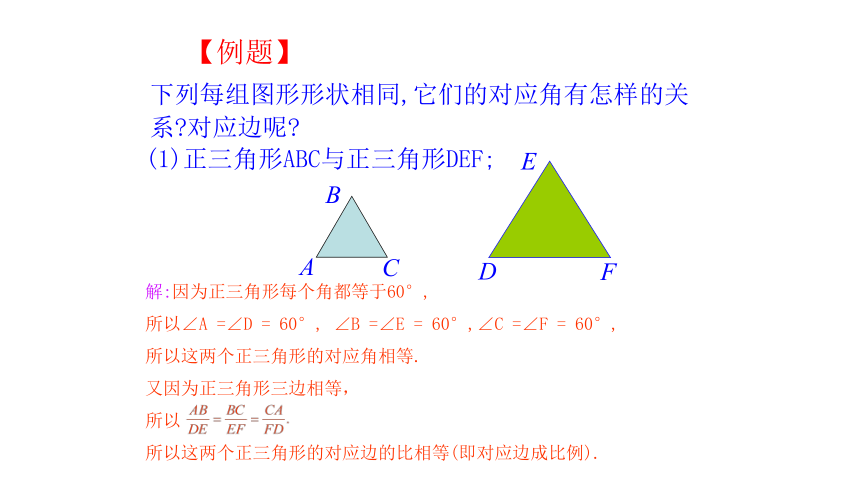
下列每组图形形状相同,它们的对应角有怎样的关系 对应边呢
(1)正三角形ABC与正三角形DEF;
解:因为正三角形每个角都等于60°,
所以∠A =∠D = 60°, ∠B =∠E = 60°,∠C =∠F = 60°,
所以这两个正三角形的对应角相等.
又因为正三角形三边相等,
所以
所以这两个正三角形的对应边的比相等(即对应边成比例).
A
B
C
D
E
F
【例题】
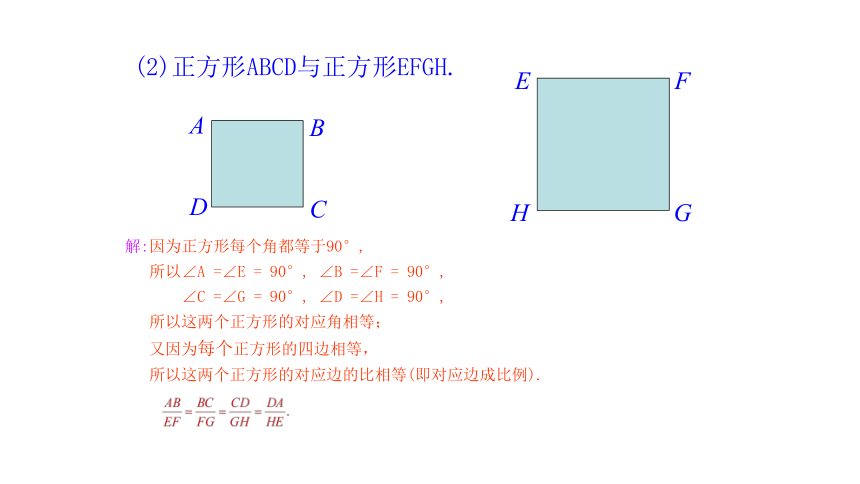
(2)正方形ABCD与正方形EFGH.
解:因为正方形每个角都等于90°,
所以∠A =∠E = 90°, ∠B =∠F = 90°,
∠C =∠G = 90°, ∠D =∠H = 90°,
所以这两个正方形的对应角相等;
又因为每个正方形的四边相等,
所以这两个正方形的对应边的比相等(即对应边成比例).
A
D
C
B
E
F
G
H
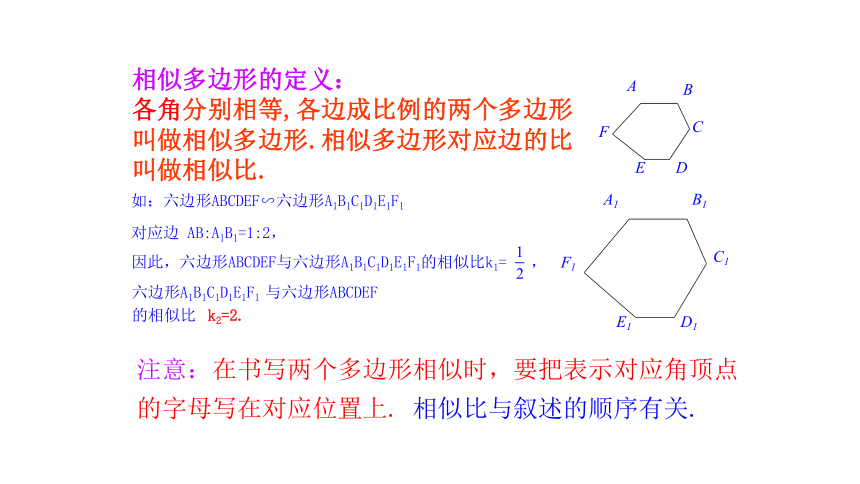
相似多边形的定义:
各角分别相等,各边成比例的两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
注意:在书写两个多边形相似时,要把表示对应角顶点的字母写在对应位置上. 相似比与叙述的顺序有关.
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
如:六边形ABCDEF∽六边形A1B1C1D1E1F1
六边形A1B1C1D1E1F1 与六边形ABCDEF
的相似比
对应边 AB:A1B1=1:2,
因此,六边形ABCDEF与六边形A1B1C1D1E1F1的相似比k1= ,
k2=2.
若两个多边形相似,那么它们的对应角相等,对应边成比例.
例:已知五边形ABCDE∽五边形A′B′C′D′E′,
它们的相似比为1:3,
(1)若∠D=135°,则∠D′=_______.
(2)若A′B′=15cm,则AB= .
135°
5cm
【做一做】
判断下列每组图形是否相似,为什么
10
正方形
10
10
正方形
10
12
12
8
12
菱形
长方形
(1)
(2)
【议一议】
解:(1)不相似.因为正方形,菱形的四条边都相等,所
以它们的对应边一定成比例,又因为正方形的
四个内角均为直角,而菱形的内角有钝角有锐
角,所以它们的对应角不相等,所以这一组图
形不相似.
(2)不相似.因为正方形和矩形的四个内角都是直
角,所以它们的对应角相等;又因为对应边
5:6≠5:4,所以对应边不成比例,所以这一组
图形不相似.
一块长3m,宽1.5m的矩形黑板如图,镶在其外围的木质边框宽7.5cm.边框的内外边缘所成的矩形相似吗 为什么
F
观察,思考,感悟是能否进入数学大门,领略数学奥妙的关键.
A
C
B
D
G
E
H
【做一做】
解: 边框的内外边缘所成的矩形不相似.理由如下:因为矩形的每个内角都等于90°,所以∠A=∠E=90°, ∠B=∠F= 90°, ∠D =∠H= 90°,∠C=∠G= 90°,
所以它们的对应角相等.
相似多边形
相似图形
相似多边形
形状相同的图形叫作相似图形
相似图形的大小不一定相同
对应角相等,对应边成比例
相似多边形对应边的比叫作相似比
1.(2021 望江期末)如图,在正方形网格上有两个
相似三角形△ABC和△EDF,则∠ABC+∠ACB的度数为
( )
A.135° B.90° C.60° D.45°
D
2.如图,小聪将一张报纸对折后,发现对折后的半
张报纸与整张报纸相似,则整张报纸的长与宽的比
是( )
A. ∶1 B.4∶1 C.2∶1 D.1.5∶1
A
3.如图,在长为8 cm、宽为4 cm的矩形中,截去一个
矩形,使得留下的矩形(图中阴影部分)与原矩形相
似,则留下的矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
C
4. 下列图形中能够确定相似的是( )
A.两个半径不相等的圆 B.所有的等边三角形
C.所有的等腰三角形 D.所有的正方形
E.所有的等腰梯形 F.所有的正六边形
ABDF
5. 若一张地图的比例尺是 1:150000,在地图上量
得甲、乙两地的距离是 5cm,则甲、乙两地的实际
距离是( )
A. 3000 m B. 3500 m
C. 5000 m D. 7500 m
D
6.一个五边形的边长分别是2,3,4,5,6,另一个
和它相似的五边形的最短边长为6,则这个五边形的
最长边长为____________.
【解析】设这个五边形的最长边长为x,则有
解得x=18.
答案:18
18
7.如图,在矩形ABCD中,点E,F分别在边AD,DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
解:因为四边形ABCD是矩形,
所以∠A=∠D=90°,
又因为AE=9,AB=6.
所以在Rt△ABE中,由勾股定理得:
BE=
因为△ABE∽△DEF,
所以 ,即
所以EF= .
人生犹如一本书,愚蠢者草草翻过,聪明人细细阅读.为何如此 因为他们只能读它一次.
——保罗
4.3 相似多边形
第四章 图形的相似
问题:用同一张底片洗出不同尺寸的照片,两张图片相似吗
情境导入
1.经历相似多边形概念的形成过程,了解相似多
边形的含义.
2.在探索相似多边形的边、角关系中,进一步发
展学生的观察、判断、归纳能力.
3.在交流和反思过程中,体验数学活动中充满了
探索性和创造性.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
观察以下两个多边形,并回答如下问题:
(1)在下图两个多边形中,是否有相等的内角 设法验证.
(2)在下图两个多边形中,相等内角的两边是否成比例
在图中,六边形ABCDEF和六边形A1B1C1D1E1F1是形状相同的图形.且
∠A与∠A1,
∠B与∠B1,
∠C与∠C1,
∠D与∠D1,
∠E与∠E1,
∠F与∠F1,
分别对应相等,称为对应角;
AB︰A1B1,
BC︰B1C1,
CD︰C1D1,
DE︰D1E1,
EF︰E1F1,
FA︰F1A1
的比都相等,称为对应边.
A
B
D
E
F
A1
B1
D1
E1
F1
C1
C
下列每组图形形状相同,它们的对应角有怎样的关系 对应边呢
(1)正三角形ABC与正三角形DEF;
解:因为正三角形每个角都等于60°,
所以∠A =∠D = 60°, ∠B =∠E = 60°,∠C =∠F = 60°,
所以这两个正三角形的对应角相等.
又因为正三角形三边相等,
所以
所以这两个正三角形的对应边的比相等(即对应边成比例).
A
B
C
D
E
F
【例题】
(2)正方形ABCD与正方形EFGH.
解:因为正方形每个角都等于90°,
所以∠A =∠E = 90°, ∠B =∠F = 90°,
∠C =∠G = 90°, ∠D =∠H = 90°,
所以这两个正方形的对应角相等;
又因为每个正方形的四边相等,
所以这两个正方形的对应边的比相等(即对应边成比例).
A
D
C
B
E
F
G
H
相似多边形的定义:
各角分别相等,各边成比例的两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
注意:在书写两个多边形相似时,要把表示对应角顶点的字母写在对应位置上. 相似比与叙述的顺序有关.
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
如:六边形ABCDEF∽六边形A1B1C1D1E1F1
六边形A1B1C1D1E1F1 与六边形ABCDEF
的相似比
对应边 AB:A1B1=1:2,
因此,六边形ABCDEF与六边形A1B1C1D1E1F1的相似比k1= ,
k2=2.
若两个多边形相似,那么它们的对应角相等,对应边成比例.
例:已知五边形ABCDE∽五边形A′B′C′D′E′,
它们的相似比为1:3,
(1)若∠D=135°,则∠D′=_______.
(2)若A′B′=15cm,则AB= .
135°
5cm
【做一做】
判断下列每组图形是否相似,为什么
10
正方形
10
10
正方形
10
12
12
8
12
菱形
长方形
(1)
(2)
【议一议】
解:(1)不相似.因为正方形,菱形的四条边都相等,所
以它们的对应边一定成比例,又因为正方形的
四个内角均为直角,而菱形的内角有钝角有锐
角,所以它们的对应角不相等,所以这一组图
形不相似.
(2)不相似.因为正方形和矩形的四个内角都是直
角,所以它们的对应角相等;又因为对应边
5:6≠5:4,所以对应边不成比例,所以这一组
图形不相似.
一块长3m,宽1.5m的矩形黑板如图,镶在其外围的木质边框宽7.5cm.边框的内外边缘所成的矩形相似吗 为什么
F
观察,思考,感悟是能否进入数学大门,领略数学奥妙的关键.
A
C
B
D
G
E
H
【做一做】
解: 边框的内外边缘所成的矩形不相似.理由如下:因为矩形的每个内角都等于90°,所以∠A=∠E=90°, ∠B=∠F= 90°, ∠D =∠H= 90°,∠C=∠G= 90°,
所以它们的对应角相等.
相似多边形
相似图形
相似多边形
形状相同的图形叫作相似图形
相似图形的大小不一定相同
对应角相等,对应边成比例
相似多边形对应边的比叫作相似比
1.(2021 望江期末)如图,在正方形网格上有两个
相似三角形△ABC和△EDF,则∠ABC+∠ACB的度数为
( )
A.135° B.90° C.60° D.45°
D
2.如图,小聪将一张报纸对折后,发现对折后的半
张报纸与整张报纸相似,则整张报纸的长与宽的比
是( )
A. ∶1 B.4∶1 C.2∶1 D.1.5∶1
A
3.如图,在长为8 cm、宽为4 cm的矩形中,截去一个
矩形,使得留下的矩形(图中阴影部分)与原矩形相
似,则留下的矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
C
4. 下列图形中能够确定相似的是( )
A.两个半径不相等的圆 B.所有的等边三角形
C.所有的等腰三角形 D.所有的正方形
E.所有的等腰梯形 F.所有的正六边形
ABDF
5. 若一张地图的比例尺是 1:150000,在地图上量
得甲、乙两地的距离是 5cm,则甲、乙两地的实际
距离是( )
A. 3000 m B. 3500 m
C. 5000 m D. 7500 m
D
6.一个五边形的边长分别是2,3,4,5,6,另一个
和它相似的五边形的最短边长为6,则这个五边形的
最长边长为____________.
【解析】设这个五边形的最长边长为x,则有
解得x=18.
答案:18
18
7.如图,在矩形ABCD中,点E,F分别在边AD,DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
解:因为四边形ABCD是矩形,
所以∠A=∠D=90°,
又因为AE=9,AB=6.
所以在Rt△ABE中,由勾股定理得:
BE=
因为△ABE∽△DEF,
所以 ,即
所以EF= .
人生犹如一本书,愚蠢者草草翻过,聪明人细细阅读.为何如此 因为他们只能读它一次.
——保罗
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
