4.6利用相似三角形测高 课件(共21张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 4.6利用相似三角形测高 课件(共21张PPT) 2024-2025学年数学北师版九年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 762.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 00:55:37 | ||
图片预览






文档简介
(共21张PPT)
第四章 图形相似
4.6 利用相似三角形测高
1.相似三角形的性质有哪些?
相似三角形的三个角相等,三边对应成比例
2.相似三角形的判定定理
本节学习目标
1.通过测量旗杆的高度,使学生综合运用三角形相似的判定条件和性质解决问题,发展学生的数学应用意识,加深学生对相似三角形的理解.
2.在分组合作活动以及全班交流过程中,使学生进一步积累数学经验和成功体验,增强学生学习数学的自信心.
如何利用相似三角形的有关知识测量旗杆(或路灯,或树,或烟囱)的高度
【议一议】
2.利用阳光下的影子,测量旗杆高度,需要测出哪些数据才能计算出高度?
方法1:利用阳光下的影子
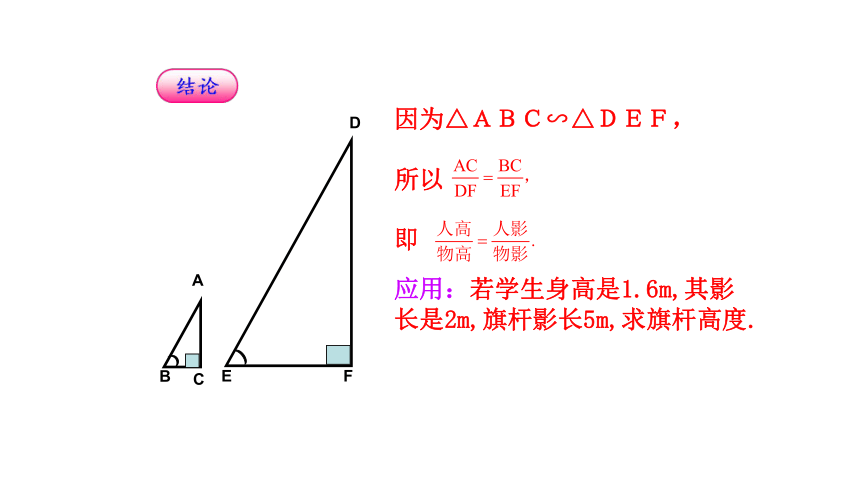
1.图中两个三角形是否相似
为什么
A
B
C
D
E
F
因为△ABC∽△DEF,
所以
即
应用:若学生身高是1.6m,其影长是2m,旗杆影长5m,求旗杆高度.
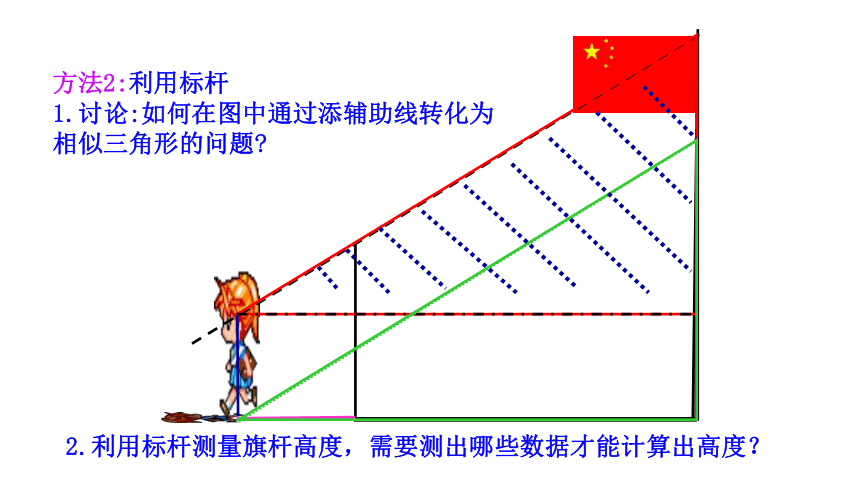
方法2:利用标杆
1.讨论:如何在图中通过添辅助线转化为相似三角形的问题
2.利用标杆测量旗杆高度,需要测出哪些数据才能计算出高度?
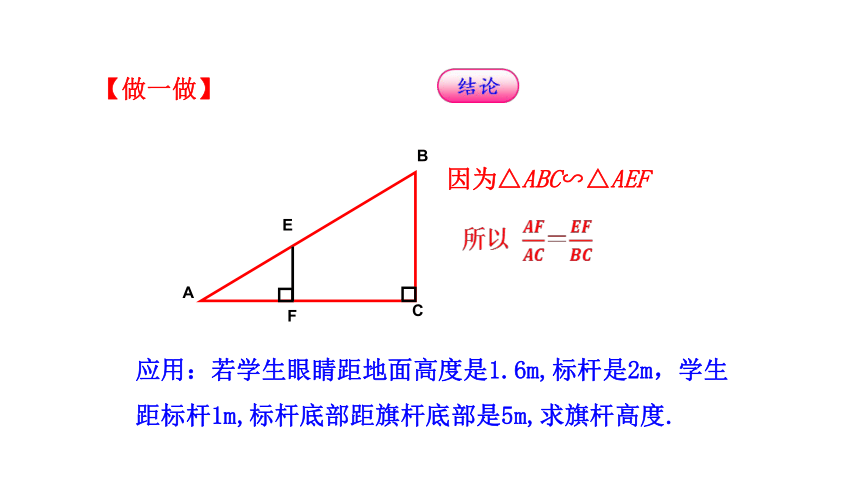
A
C
B
E
F
因为△ABC∽△AEF
应用:若学生眼睛距地面高度是1.6m,标杆是2m,学生距标杆1m,标杆底部距旗杆底部是5m,求旗杆高度.
【做一做】
方法3:利用镜子
1.图中的两个三角形是否相似 为什么?
2.利用镜子反射测量旗杆高度,需要
测出哪些数据才能计算出高度?
【议一议】
E
C
B
D
A
因为△ADE∽△ABC
所以 =
AE DE
AC BC
应用:若学生眼睛距地面高度是1.6m,学生脚距镜子1m,镜子距旗杆底部是5m,求旗杆高度.
【做一做】
1.如图,在距离AB 18m的地面上平放着一面镜子E,人退后到距镜子2.1m的D处,在镜子里恰看见树顶,若人眼距地面1.4m,求树高.
解:设树高xm.
由题意知△ABE∽△CDE,
所以
x=12.
答:树高12m.
18m
1.4m
2.1m
1
2
D
B
C
E
A
【跟踪训练】
2.如图,A,B两点分别位于一个池塘的两端,小芳想用绳子测量A,B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A,B两点的点C,找到AC,BC的中点D,E,若DE的长为5m,则A,B两点的距离是多少?
解:由题意知△CDE∽△CAB,
所以AB=10.
答:A,B两点间的距离是10m.
5m
C
B
A
E
D
通过本课时的学习,需要我们掌握:
1.利用阳光下的影子、标杆和镜子的反射,测量旗杆的高度.
2.当被测物体不能直接测量时,我们往往利用相似三角形的性质测量物体.
3.利用这三种测量方法,测量的结果允许有误差.
1.(2021 越秀区月考)下列图形不是相似图形的
是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和
放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
C
2.(2021 兰州期末)某数学兴趣小组来到城关区时代广场,
设计用手电来测量广场附近某大厦CD的高度,如图,点P处放
一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大
厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2
米,PD=52米,那么该大厦的高度约为( )
A.39米 B.30米 C.24米 D.15米
A
3.(2021 天桥期末)如图所示,某校数学兴趣小组利用标杆
BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,
BC=7m,则建筑物CD的高是( )
A.3.5m B.4m C.4.5m D.5m
D
4.(2021 芜湖模拟)如图所示,小明在地面上放置一个平面镜C,选择合适的位置,刚好在平面镜C中看到旗杆DE的顶部,此时小明与平面镜C的水平距离BC为2m,旗杆底部与平面镜的水平距离CE为16m.若小明的眼睛与地面的距离AB为1.6m,试求旗杆DE的高度.
【分析】如图,BC=2m,CE=16m,AB=1.6m,利用题意得∠ACB=∠DCE,则可判断△ACB∽△DCE,然后利用相似比计算出DE的长.
解:由题意得∠ACB=∠DCE,
∵∠ABC=∠DEC,
∴△ACB∽△DCE,
∴DE=12.8
答:旗杆的高度为12.8m.
∴ ,即 .
5.(2021 陕西模拟)如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB,GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计)
解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴OE=OA+4,
答:大树的高度OE为12m.
∴OE=1.5OA,
∴1.5OA=OA+4,
∴OA=8m,OE=12m.
把语言化为行动,比把行动化为语言困难得多。 ———高尔基
第四章 图形相似
4.6 利用相似三角形测高
1.相似三角形的性质有哪些?
相似三角形的三个角相等,三边对应成比例
2.相似三角形的判定定理
本节学习目标
1.通过测量旗杆的高度,使学生综合运用三角形相似的判定条件和性质解决问题,发展学生的数学应用意识,加深学生对相似三角形的理解.
2.在分组合作活动以及全班交流过程中,使学生进一步积累数学经验和成功体验,增强学生学习数学的自信心.
如何利用相似三角形的有关知识测量旗杆(或路灯,或树,或烟囱)的高度
【议一议】
2.利用阳光下的影子,测量旗杆高度,需要测出哪些数据才能计算出高度?
方法1:利用阳光下的影子
1.图中两个三角形是否相似
为什么
A
B
C
D
E
F
因为△ABC∽△DEF,
所以
即
应用:若学生身高是1.6m,其影长是2m,旗杆影长5m,求旗杆高度.
方法2:利用标杆
1.讨论:如何在图中通过添辅助线转化为相似三角形的问题
2.利用标杆测量旗杆高度,需要测出哪些数据才能计算出高度?
A
C
B
E
F
因为△ABC∽△AEF
应用:若学生眼睛距地面高度是1.6m,标杆是2m,学生距标杆1m,标杆底部距旗杆底部是5m,求旗杆高度.
【做一做】
方法3:利用镜子
1.图中的两个三角形是否相似 为什么?
2.利用镜子反射测量旗杆高度,需要
测出哪些数据才能计算出高度?
【议一议】
E
C
B
D
A
因为△ADE∽△ABC
所以 =
AE DE
AC BC
应用:若学生眼睛距地面高度是1.6m,学生脚距镜子1m,镜子距旗杆底部是5m,求旗杆高度.
【做一做】
1.如图,在距离AB 18m的地面上平放着一面镜子E,人退后到距镜子2.1m的D处,在镜子里恰看见树顶,若人眼距地面1.4m,求树高.
解:设树高xm.
由题意知△ABE∽△CDE,
所以
x=12.
答:树高12m.
18m
1.4m
2.1m
1
2
D
B
C
E
A
【跟踪训练】
2.如图,A,B两点分别位于一个池塘的两端,小芳想用绳子测量A,B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A,B两点的点C,找到AC,BC的中点D,E,若DE的长为5m,则A,B两点的距离是多少?
解:由题意知△CDE∽△CAB,
所以AB=10.
答:A,B两点间的距离是10m.
5m
C
B
A
E
D
通过本课时的学习,需要我们掌握:
1.利用阳光下的影子、标杆和镜子的反射,测量旗杆的高度.
2.当被测物体不能直接测量时,我们往往利用相似三角形的性质测量物体.
3.利用这三种测量方法,测量的结果允许有误差.
1.(2021 越秀区月考)下列图形不是相似图形的
是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和
放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
C
2.(2021 兰州期末)某数学兴趣小组来到城关区时代广场,
设计用手电来测量广场附近某大厦CD的高度,如图,点P处放
一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大
厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2
米,PD=52米,那么该大厦的高度约为( )
A.39米 B.30米 C.24米 D.15米
A
3.(2021 天桥期末)如图所示,某校数学兴趣小组利用标杆
BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,
BC=7m,则建筑物CD的高是( )
A.3.5m B.4m C.4.5m D.5m
D
4.(2021 芜湖模拟)如图所示,小明在地面上放置一个平面镜C,选择合适的位置,刚好在平面镜C中看到旗杆DE的顶部,此时小明与平面镜C的水平距离BC为2m,旗杆底部与平面镜的水平距离CE为16m.若小明的眼睛与地面的距离AB为1.6m,试求旗杆DE的高度.
【分析】如图,BC=2m,CE=16m,AB=1.6m,利用题意得∠ACB=∠DCE,则可判断△ACB∽△DCE,然后利用相似比计算出DE的长.
解:由题意得∠ACB=∠DCE,
∵∠ABC=∠DEC,
∴△ACB∽△DCE,
∴DE=12.8
答:旗杆的高度为12.8m.
∴ ,即 .
5.(2021 陕西模拟)如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB,GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计)
解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴OE=OA+4,
答:大树的高度OE为12m.
∴OE=1.5OA,
∴1.5OA=OA+4,
∴OA=8m,OE=12m.
把语言化为行动,比把行动化为语言困难得多。 ———高尔基
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
