6.2反比例函数的图象与性质(第2课时)课件(共24张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 6.2反比例函数的图象与性质(第2课时)课件(共24张PPT) 2024-2025学年数学北师版九年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 01:03:00 | ||
图片预览





文档简介
(共24张PPT)
(第2课时)
2 反比例函数的图象与性质
O
x
y
第六章 反比例函数
1.写出反比例函数的表达式:________________.
2.反比例函数的图象是__________.
3.反比例函数 的图象在第_________象限内.
4.反比例函数 经过点(m,2),则m的值为____.
5.反比例函数 的图象经过点(2,-3), 则它的达
式为__________.
双曲线
2
二、四
1.通过图象探索反比例函数的主要性质.
2.逐步提高从函数图象获取信息的能力,会运用数形结合的思想方法解决涉及反比例函数的有关问题.
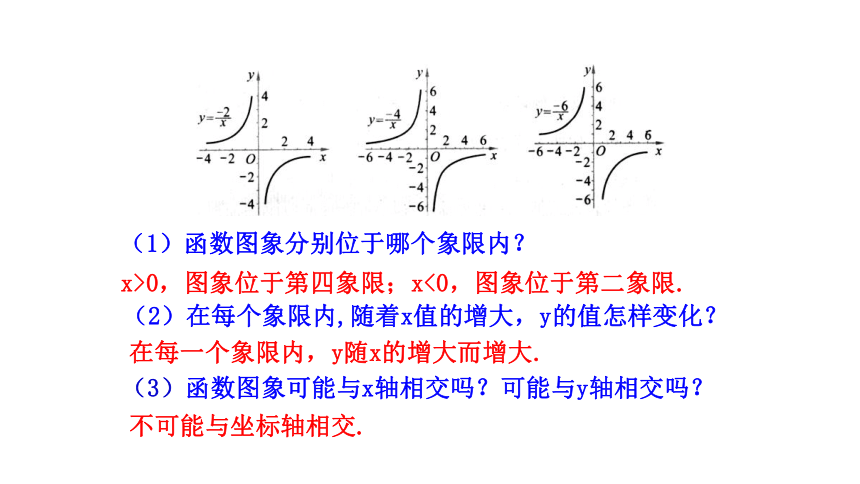
(1)函数图象分别位于哪几个象限?
第一、三象限内
x>0,图象位于第一象限;x<0,图象位于第三象限.
在每一个象限内,y随x的增大而减小.
(2)当x取什么值时,图象位于第一象限?当x取什么值时,图象位于第三象限?
(3)在每个象限内,随着x值的增大,y的值怎样变化?
1.反比例函数是一个怎样的图象?
2.反比例函数的图象的位置与k有怎样的关系?
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线.
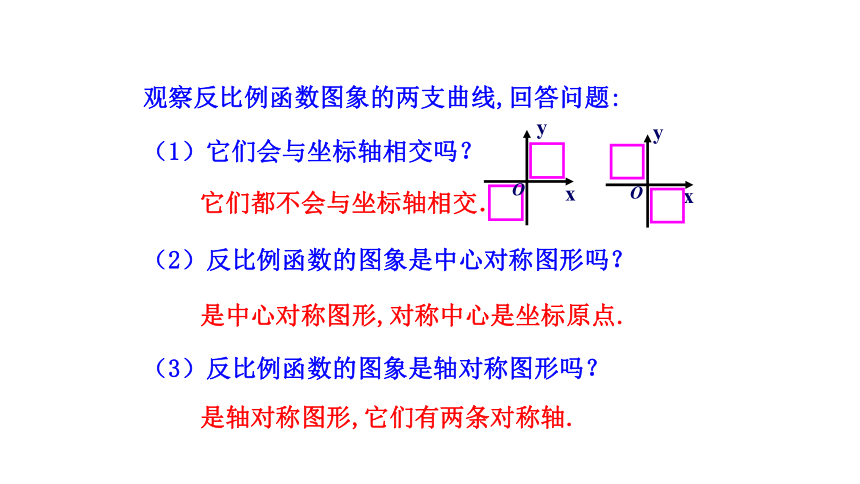
(1)函数图象分别位于哪个象限内?
x>0,图象位于第四象限;x<0,图象位于第二象限.
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一个象限内,y随x的增大而增大.
(3)函数图象可能与x轴相交吗?可能与y轴相交吗?
不可能与坐标轴相交.
观察反比例函数图象的两支曲线,回答问题:
(1)它们会与坐标轴相交吗?
(2)反比例函数的图象是中心对称图形吗?
(3)反比例函数的图象是轴对称图形吗?
它们都不会与坐标轴相交.
是轴对称图形,它们有两条对称轴.
是中心对称图形,对称中心是坐标原点.
x
y
O
x
y
O
⑴当k>0时,两支曲线分别位于第一、三象限
内,在每一象限内,y的值随x值的增大而减小.
1.反比例函数的图象是双曲线.
⑵当k<0时,两支曲线分别位于第二、四象限
内,在每一象限内,y的值随x值的增大而增大.
x
y
O
x
y
【结论】
O
2.双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交.
3.图象的两个分支关于原点对称.
O
x
y
O
x
y
1.下列函数中,其图象位于第一、三象限的有__________________;
在其所在的象限内,y随x的增大而增大的有_____.
(1)(2)(3)
(4)
【跟踪训练】
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函
数 的图象上,比较y1、 y2 、y3的大小关系.
【解析】∵k=4>0,
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵-2<-1<0,3>0,
∴点A(-2,y1),点B(-1,y2)在第三象限,点C(3,y3)在第一象限.
∴y3>0, y2【解析】当k>0时, y2 < y1 < y3 ;
当k<0时, y3 < y1 < y2.
(2)如果点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函
数 的图象上,那么y1、 y2 、y3的大小关系又如何呢?
O
x
y
O
x
y
在一个反比例函数图象上任意取两点P,Q,过点P,Q分别作x轴和y轴的平行线,与坐标轴围成的矩形面积分别记为S1和S2,则S1和S2之间有什么关系?说明理由.
想一想
P
Q
S1
S2
S1、S2有什么关系?
为什么?
R
S3
S1=S2,
S1、S2、S3有什么关系?
S1=S2=S3
函数 正比例函数 反比例函数
表达式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y=
x
k
直线
双曲线
一、三象限
y随x的增大而增大
一、三象限
每个象限内, y随x的增大而减小
二、四象限
二、四象限
y随x的增大而减小
每个象限内, y随x的增大而增大
x
y
O
x
y
O
x
y
O
x
y
O
反比例函数
的性质
性质
反比例函数图象中比例系数k的几何意义
当k>0时,在每一象限内,
y的值随x的增大而减小.
当k<0时,在每一象限内,
y的值随x的增大而增大.
A
2.(2021 河口质检)若图中反比例函数的表达式均为y= ,
则阴影面积为4的有( )
A.1个 B.2个 C.3个 D.4个
B
增大
努力向前,默默耕耘,机会和成功必属于最坚韧的奋斗者.
——佚名
(第2课时)
2 反比例函数的图象与性质
O
x
y
第六章 反比例函数
1.写出反比例函数的表达式:________________.
2.反比例函数的图象是__________.
3.反比例函数 的图象在第_________象限内.
4.反比例函数 经过点(m,2),则m的值为____.
5.反比例函数 的图象经过点(2,-3), 则它的达
式为__________.
双曲线
2
二、四
1.通过图象探索反比例函数的主要性质.
2.逐步提高从函数图象获取信息的能力,会运用数形结合的思想方法解决涉及反比例函数的有关问题.
(1)函数图象分别位于哪几个象限?
第一、三象限内
x>0,图象位于第一象限;x<0,图象位于第三象限.
在每一个象限内,y随x的增大而减小.
(2)当x取什么值时,图象位于第一象限?当x取什么值时,图象位于第三象限?
(3)在每个象限内,随着x值的增大,y的值怎样变化?
1.反比例函数是一个怎样的图象?
2.反比例函数的图象的位置与k有怎样的关系?
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线.
(1)函数图象分别位于哪个象限内?
x>0,图象位于第四象限;x<0,图象位于第二象限.
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一个象限内,y随x的增大而增大.
(3)函数图象可能与x轴相交吗?可能与y轴相交吗?
不可能与坐标轴相交.
观察反比例函数图象的两支曲线,回答问题:
(1)它们会与坐标轴相交吗?
(2)反比例函数的图象是中心对称图形吗?
(3)反比例函数的图象是轴对称图形吗?
它们都不会与坐标轴相交.
是轴对称图形,它们有两条对称轴.
是中心对称图形,对称中心是坐标原点.
x
y
O
x
y
O
⑴当k>0时,两支曲线分别位于第一、三象限
内,在每一象限内,y的值随x值的增大而减小.
1.反比例函数的图象是双曲线.
⑵当k<0时,两支曲线分别位于第二、四象限
内,在每一象限内,y的值随x值的增大而增大.
x
y
O
x
y
【结论】
O
2.双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交.
3.图象的两个分支关于原点对称.
O
x
y
O
x
y
1.下列函数中,其图象位于第一、三象限的有__________________;
在其所在的象限内,y随x的增大而增大的有_____.
(1)(2)(3)
(4)
【跟踪训练】
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函
数 的图象上,比较y1、 y2 、y3的大小关系.
【解析】∵k=4>0,
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵-2<-1<0,3>0,
∴点A(-2,y1),点B(-1,y2)在第三象限,点C(3,y3)在第一象限.
∴y3>0, y2
当k<0时, y3 < y1 < y2.
(2)如果点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函
数 的图象上,那么y1、 y2 、y3的大小关系又如何呢?
O
x
y
O
x
y
在一个反比例函数图象上任意取两点P,Q,过点P,Q分别作x轴和y轴的平行线,与坐标轴围成的矩形面积分别记为S1和S2,则S1和S2之间有什么关系?说明理由.
想一想
P
Q
S1
S2
S1、S2有什么关系?
为什么?
R
S3
S1=S2,
S1、S2、S3有什么关系?
S1=S2=S3
函数 正比例函数 反比例函数
表达式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y=
x
k
直线
双曲线
一、三象限
y随x的增大而增大
一、三象限
每个象限内, y随x的增大而减小
二、四象限
二、四象限
y随x的增大而减小
每个象限内, y随x的增大而增大
x
y
O
x
y
O
x
y
O
x
y
O
反比例函数
的性质
性质
反比例函数图象中比例系数k的几何意义
当k>0时,在每一象限内,
y的值随x的增大而减小.
当k<0时,在每一象限内,
y的值随x的增大而增大.
A
2.(2021 河口质检)若图中反比例函数的表达式均为y= ,
则阴影面积为4的有( )
A.1个 B.2个 C.3个 D.4个
B
增大
努力向前,默默耕耘,机会和成功必属于最坚韧的奋斗者.
——佚名
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
