人教版数学八年级下册18.2.3正方形的判定教学设计
文档属性
| 名称 | 人教版数学八年级下册18.2.3正方形的判定教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 47.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 14:52:06 | ||
图片预览


文档简介
《正方形的判定》教学设计
一:教材分析
《正方形的判定》是人教版数学八年级下册第18章第2节特殊的平行四边形第六课时。本节课注重新旧知识的联系与对比,注重图形的分析,判别。在学行四边形,矩形,菱形的性质与判定以及正方形的性质的基础上,引入了正方形的判定,这节课既是前面所学知识的延续,又是对平行四边形,矩形,菱形的判定进行综合的不可缺少的重要环节。
二:教学目标
知道正方形的判定方法,会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算。经历探究正方形判定条件的过程,发展学生初步的综合推理能力,主动探究的学习习 惯,逐步掌握说理的基本方法。理解特殊的平行四边形之间的内在联系,培养学生辩证看问题的观点。
三:教学重难点
教学重点:掌握正方形的判定条件。
教学难点:正方形判定方法的应用。
四:学生学情分析
学生已经较为系统的学行四边形、矩形、菱形的基本性质与判定,已经具有了四边形的基本认知与知识结构,这些已有的认知结构可以迁移到正方形的学习中来。在相关知识的学习过程中,学生已经经历了一些对四边形探索的具体方法,并能解决一些简单的现实问题,感受到数学信息的收集和处理的必要性和作用,获得了从事探究活动所必须的一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
五:教学策略分析
本节课虽然内容不多,但是与前面内容平行四边形,菱形,矩形的判定进行综合,对学生的逆向思维与推理能力要求比较高,针对本班的学生的知识结构与心理特点,我采用了“提前预习+多媒体教学”,运用了“情境引入、合作交流、引导提问、归纳论证、深化巩固”的启发式教学方法。教学中,引导学生经历类比归纳的过程,充分感受教学思维的特点,进一步提高逻辑推理能力,增强探索新知的兴趣。
六:教学过程
第一环节:复习回顾
正方形的定义:有一个角是直角且一组邻边相等的平行四边形是正方形。
正方形的性质:
边:正方形的对边平行且相等
角:正方形的四个角都是直角
对角线:正方形的对角线互相垂直平分且相等,每条对角线平分一组对角。
师生一起回顾,并要求学生不要看书,看谁回顾的准确。
通过创设情境,引导学生回顾旧知识,在掌握正方形的定义的基础上,进一步探索正方形的判定的方法,引出本课主题。
第二环节:讲授新课
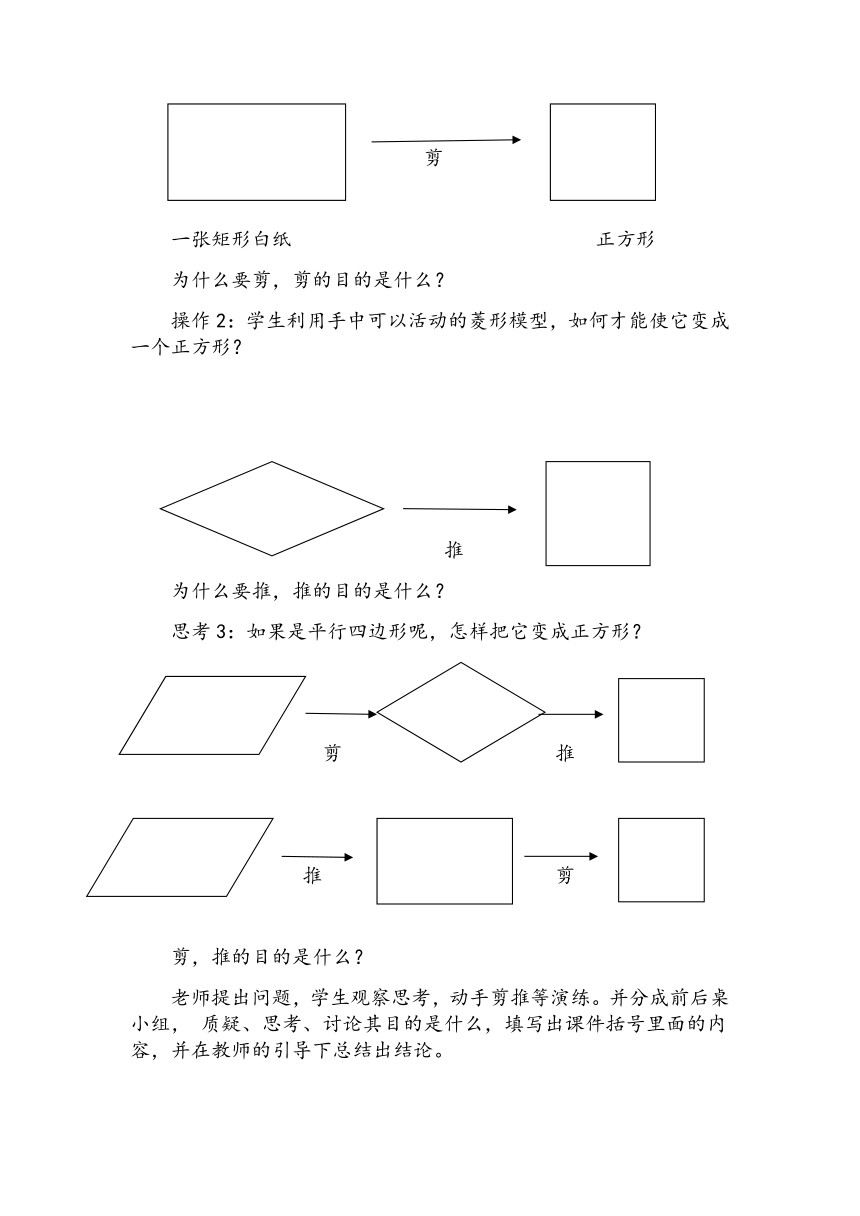
操作1:每个同学手里准备一张矩形白纸,如何让它变成一个正方形?
剪
一张矩形白纸 正方形
为什么要剪,剪的目的是什么?
操作2:学生利用手中可以活动的菱形模型,如何才能使它变成一个正方形?
推
为什么要推,推的目的是什么?
思考3:如果是平行四边形呢,怎样把它变成正方形?
剪 推
推 剪
剪,推的目的是什么?
老师提出问题,学生观察思考,动手剪推等演练。并分成前后桌小组, 质疑、思考、讨论其目的是什么,填写出课件括号里面的内容,并在教师的引导下总结出结论。
通过这一活动,让学生感受到生活中的数学,引起学生学习兴趣,更加深刻的理解正方形的判定方法。
总结4:归纳总结出正方形的判定方法:
定义法:有一个角是直角且一组邻边相等的平行四边形。
菱形法:有一个角是直角的菱形是正方形。
矩形法:有一组邻边相等的矩形是正方形。
老师引导,学生根据操作1、2、3总结出正方形的判定方法。让学生对正方形的判定方法知识,有了一个完整的明确的印象,培养了学生的记忆归纳和表达能力。
第三环节:议一议
我们学习了四边形,平行四边形,菱形,矩形,正方形,那么思考一下,它们之间有怎样的包含关系呢?
通过填写让学生形象的看到正方形是特殊的矩形,也是特殊的菱形,还是特殊的平行四边形,而正方形、菱形、矩形都是平行四边形,菱形、矩形也是特殊的平行四边形,正方形、菱形、矩形、平行四边形都是四边形。
1:怎样判断一个四边形是平行四边形?
2:怎样判断一个四边形是菱形?
3:怎样判断一个四边形是矩形?
4:怎样判断一个四边形是正方形?
这些都是我们以前学习过的,今天通过议一议,比一比,通过小组竞猜的模式看谁的答案对且多,回答4的问题。
通过竞赛的模式能更加激发学生的主动探索的求知欲,让学生通过自己的思考得出来的结论会让其记忆更深刻,理解更透彻。
第四环节:自我检测
这一环节的题目我分了两部分,第一部分“我选择,我喜欢”都是一些相对简单的题目,我会找平时学习成绩不是太好的学生,让他们也能得到很好的认可。第二部分“奔跑吧,挑战者”是一些相对有一些难度的题目。这样题目有了梯度和层次,更有针对性。
“我选择,我喜欢”有六个题目,分别被六个可爱的小动物掌管,四道题目是判断,两道题目是选择。学生思考探究解决问题的思路与方法,教师针对学生的解答情况进行讲解。这道题意在对正方形判定方法更进一步巩固,并能让教师及时对学生所学知识的应用有个反馈作用。让学生经历运用知识解决问题的过程,给学生获得成功体验的空间,激发学习的积极性,建立学好数学的信心。
“奔跑吧,挑战者”有3个题目:
1.已知:在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.
求证: 四边形CFDE是正方形.
2.已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6 cm,面积S=________.则边长AB=____
3.如图,正方形ABCD的周长为15cm,则矩形EFCG的周长为 ________cm。
通过这样的训练,分析证明题的方法,可以扩大学生的思维能力,培养学生的动手能力,动脑分析问题的能力,培养学生的逻辑推理能力。
第五环节:归纳总结
本节课学习了哪些内容,谈谈你们的感受。
教师鼓励学生积极发言,进行归纳,教师可补充进行说明。通过学生对本节课所学内容的自我归纳,总结,加深了“正方形判定方法”的理解及应用,使学生对所学知识形成了一个完整的知识体系。
七:教学反思
在教学设计上,我依据教材、《新课标》及学生实际情况,坚持了以学生为中心的教学思想,运用了探究式,开放式的教学方法,通过学生们的亲自动手演示得到相应的结论,让他们大胆的放开思维,再通过老师亲切的语言互动,使学生们在欢乐的气氛中得到知识,掌握知识。我觉得只有这样学生们才能真正的爱上数学,把学到的知识牢牢的记住。
八:板书设计:
正方形的判定
矩形 正方形
菱形 正方形
平行四边形 正方形
四边形 正方形
一:教材分析
《正方形的判定》是人教版数学八年级下册第18章第2节特殊的平行四边形第六课时。本节课注重新旧知识的联系与对比,注重图形的分析,判别。在学行四边形,矩形,菱形的性质与判定以及正方形的性质的基础上,引入了正方形的判定,这节课既是前面所学知识的延续,又是对平行四边形,矩形,菱形的判定进行综合的不可缺少的重要环节。
二:教学目标
知道正方形的判定方法,会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算。经历探究正方形判定条件的过程,发展学生初步的综合推理能力,主动探究的学习习 惯,逐步掌握说理的基本方法。理解特殊的平行四边形之间的内在联系,培养学生辩证看问题的观点。
三:教学重难点
教学重点:掌握正方形的判定条件。
教学难点:正方形判定方法的应用。
四:学生学情分析
学生已经较为系统的学行四边形、矩形、菱形的基本性质与判定,已经具有了四边形的基本认知与知识结构,这些已有的认知结构可以迁移到正方形的学习中来。在相关知识的学习过程中,学生已经经历了一些对四边形探索的具体方法,并能解决一些简单的现实问题,感受到数学信息的收集和处理的必要性和作用,获得了从事探究活动所必须的一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
五:教学策略分析
本节课虽然内容不多,但是与前面内容平行四边形,菱形,矩形的判定进行综合,对学生的逆向思维与推理能力要求比较高,针对本班的学生的知识结构与心理特点,我采用了“提前预习+多媒体教学”,运用了“情境引入、合作交流、引导提问、归纳论证、深化巩固”的启发式教学方法。教学中,引导学生经历类比归纳的过程,充分感受教学思维的特点,进一步提高逻辑推理能力,增强探索新知的兴趣。
六:教学过程
第一环节:复习回顾
正方形的定义:有一个角是直角且一组邻边相等的平行四边形是正方形。
正方形的性质:
边:正方形的对边平行且相等
角:正方形的四个角都是直角
对角线:正方形的对角线互相垂直平分且相等,每条对角线平分一组对角。
师生一起回顾,并要求学生不要看书,看谁回顾的准确。
通过创设情境,引导学生回顾旧知识,在掌握正方形的定义的基础上,进一步探索正方形的判定的方法,引出本课主题。
第二环节:讲授新课
操作1:每个同学手里准备一张矩形白纸,如何让它变成一个正方形?
剪
一张矩形白纸 正方形
为什么要剪,剪的目的是什么?
操作2:学生利用手中可以活动的菱形模型,如何才能使它变成一个正方形?
推
为什么要推,推的目的是什么?
思考3:如果是平行四边形呢,怎样把它变成正方形?
剪 推
推 剪
剪,推的目的是什么?
老师提出问题,学生观察思考,动手剪推等演练。并分成前后桌小组, 质疑、思考、讨论其目的是什么,填写出课件括号里面的内容,并在教师的引导下总结出结论。
通过这一活动,让学生感受到生活中的数学,引起学生学习兴趣,更加深刻的理解正方形的判定方法。
总结4:归纳总结出正方形的判定方法:
定义法:有一个角是直角且一组邻边相等的平行四边形。
菱形法:有一个角是直角的菱形是正方形。
矩形法:有一组邻边相等的矩形是正方形。
老师引导,学生根据操作1、2、3总结出正方形的判定方法。让学生对正方形的判定方法知识,有了一个完整的明确的印象,培养了学生的记忆归纳和表达能力。
第三环节:议一议
我们学习了四边形,平行四边形,菱形,矩形,正方形,那么思考一下,它们之间有怎样的包含关系呢?
通过填写让学生形象的看到正方形是特殊的矩形,也是特殊的菱形,还是特殊的平行四边形,而正方形、菱形、矩形都是平行四边形,菱形、矩形也是特殊的平行四边形,正方形、菱形、矩形、平行四边形都是四边形。
1:怎样判断一个四边形是平行四边形?
2:怎样判断一个四边形是菱形?
3:怎样判断一个四边形是矩形?
4:怎样判断一个四边形是正方形?
这些都是我们以前学习过的,今天通过议一议,比一比,通过小组竞猜的模式看谁的答案对且多,回答4的问题。
通过竞赛的模式能更加激发学生的主动探索的求知欲,让学生通过自己的思考得出来的结论会让其记忆更深刻,理解更透彻。
第四环节:自我检测
这一环节的题目我分了两部分,第一部分“我选择,我喜欢”都是一些相对简单的题目,我会找平时学习成绩不是太好的学生,让他们也能得到很好的认可。第二部分“奔跑吧,挑战者”是一些相对有一些难度的题目。这样题目有了梯度和层次,更有针对性。
“我选择,我喜欢”有六个题目,分别被六个可爱的小动物掌管,四道题目是判断,两道题目是选择。学生思考探究解决问题的思路与方法,教师针对学生的解答情况进行讲解。这道题意在对正方形判定方法更进一步巩固,并能让教师及时对学生所学知识的应用有个反馈作用。让学生经历运用知识解决问题的过程,给学生获得成功体验的空间,激发学习的积极性,建立学好数学的信心。
“奔跑吧,挑战者”有3个题目:
1.已知:在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.
求证: 四边形CFDE是正方形.
2.已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6 cm,面积S=________.则边长AB=____
3.如图,正方形ABCD的周长为15cm,则矩形EFCG的周长为 ________cm。
通过这样的训练,分析证明题的方法,可以扩大学生的思维能力,培养学生的动手能力,动脑分析问题的能力,培养学生的逻辑推理能力。
第五环节:归纳总结
本节课学习了哪些内容,谈谈你们的感受。
教师鼓励学生积极发言,进行归纳,教师可补充进行说明。通过学生对本节课所学内容的自我归纳,总结,加深了“正方形判定方法”的理解及应用,使学生对所学知识形成了一个完整的知识体系。
七:教学反思
在教学设计上,我依据教材、《新课标》及学生实际情况,坚持了以学生为中心的教学思想,运用了探究式,开放式的教学方法,通过学生们的亲自动手演示得到相应的结论,让他们大胆的放开思维,再通过老师亲切的语言互动,使学生们在欢乐的气氛中得到知识,掌握知识。我觉得只有这样学生们才能真正的爱上数学,把学到的知识牢牢的记住。
八:板书设计:
正方形的判定
矩形 正方形
菱形 正方形
平行四边形 正方形
四边形 正方形
