1.2 怎样判定三角形相似(第4课时) 课件(共21张PPT)
文档属性
| 名称 | 1.2 怎样判定三角形相似(第4课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 734.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 06:56:38 | ||
图片预览








文档简介
(共21张PPT)
(青岛版)9年级
上
1.2怎样判定三角形相似(第4课时)
第1章
“—”
二、相似三角形的判定方法:
3、判定定理1
还有其它
判定方法吗?
一、相似三角形的定义:
1、定义法:
2、平行线法:
三、相似三角形的性质:
1.对应角的关系
2.对应边的关系
4、判定定理2
复习回顾
1、能识别两个三角形相似的方法:有两边对应成比例,且夹角相等的两个三角形相似;三条边对应成比例的两个三角形相似.
2、能依据条件,灵活运用三种识别方法,正确判断两个三角形相似.
3、在推理过程中学会灵活使用数学方法.
学习目标
1.在前面的学习中,我们学过哪些判定三角形相似的方法?
1.定义法:
对应角相等、对应边成比例的两个三角形相似.
2.预备定理:
平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3.(AA)两个角对应相等的两个三角形相似.
类似于判定三角形全等的SSS方法,能不能通过三边对应成比例来判定两个三角形相似呢?
4.(SAS)两边对应成比例且夹角相等,两三角形相似.
新知导入
A
B
C
A′
B′
C′
提示:
能形成A型或X型吗?
(1)在AB边上截取AD=A′B′;
(2)过点D作DE∥BC,交AC于点E;
问:(1)△ADE与△ABC相似吗?
(2)△ADE与△A′B′C′全等吗?
D.
E
所以,△ABC∽△A′B′C′
在△ABC和△A′B′C′中,若
那么△ABC∽△A′B′C′吗?
新知探究
相似三角形的判定定理3
三边对应成比例的两三角形相似。
△ABC∽△A'B'C'.
A'
B'
C'
A
B
C
在△A′B′C'与△ABC中:
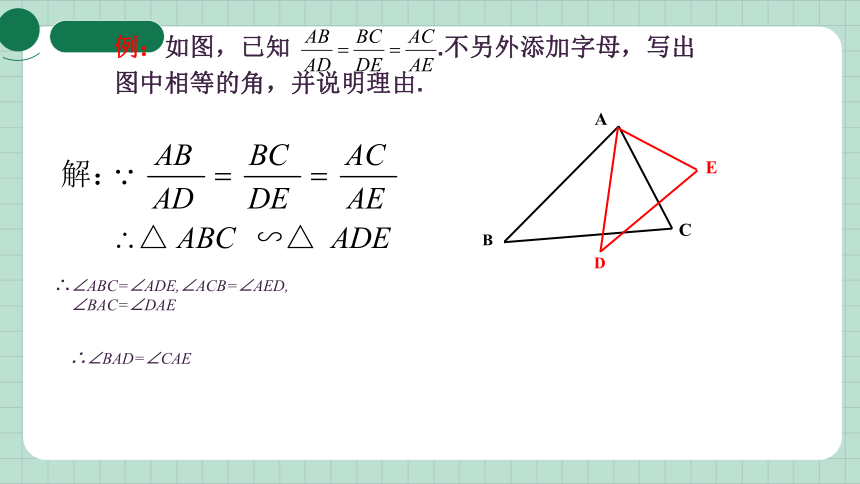
例:如图,已知 .不另外添加字母,写出 图中相等的角,并说明理由.
A
C
B
D
E
例:如图,已知 .不另外添加字母,写出 图中相等的角,并说明理由.
A
C
B
D
E
∴∠ABC=∠ADE,∠ACB=∠AED,
∠BAC=∠DAE
∴∠BAD=∠CAE
看已知条件
判定相似
选方法
找够判定方法
中所需的条件
1.下列条件中,能判定△ABC与△DEF相似的有( )
①∠A=45°,AB=12,AC=15,∠D=45°,DE=16,DF=40;
②AB=12,BC=15,AC=24,DE=20,EF=25,DF=40;
③∠A=47°,AB=15,AC=20,∠E=47°,DE=28,EF=21.
A.0个 B.1个
C.2个 D.3个
C
课堂练习
2、图中的两个三角形是否相似?
15
25
20
27
45
40
A
B
C
D
E
45
54
36
30
2、图中的两个三角形是否相似?
15
25
20
27
45
40
A
B
C
D
E
45
54
36
30
∴△ACB∽△ECD
对应边的比不相等
∴图中两个三角形不相似.
对应边的比不相等
A
B
C
D
E
F
3.如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC∽△DEF.
5
12
8
10
A
B
C
D
E
F
3.如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC∽△DEF.
5
12
8
10
16
24
A
B
C
D
E
4.如图,在 △ABC 和 △ADE 中, ,∠BAD=20°,求∠CAE的度数.
∴∠CAE=20°.
A
B
C
D
E
4.如图,在 △ABC 和 △ADE 中, ,∠BAD=20°,求∠CAE的度数.
解:
∴ △ABC ∽△ADE
∴ ∠BAC=∠DAE,
∴∠BAC -∠DAC=∠DAE -∠DAC,
即 ∠BAD=∠CAE.
又∵∠BAD=20°,
∵
判定三角形相似的方法
定义
判定定理1
判定定理2
判定定理3
平行线法
课堂总结
1、课本18练习1,2
2、习题1.2,T2-5
作业布置
A
B
C
O
A′
。
B′
。
C′
。
3、已知:如图,AA′、BB′、CC′相交于点O,且
求证:△ABC∽△A′B′C′
2
https://www.21cnjy.com/help/help_extract.php
(青岛版)9年级
上
1.2怎样判定三角形相似(第4课时)
第1章
“—”
二、相似三角形的判定方法:
3、判定定理1
还有其它
判定方法吗?
一、相似三角形的定义:
1、定义法:
2、平行线法:
三、相似三角形的性质:
1.对应角的关系
2.对应边的关系
4、判定定理2
复习回顾
1、能识别两个三角形相似的方法:有两边对应成比例,且夹角相等的两个三角形相似;三条边对应成比例的两个三角形相似.
2、能依据条件,灵活运用三种识别方法,正确判断两个三角形相似.
3、在推理过程中学会灵活使用数学方法.
学习目标
1.在前面的学习中,我们学过哪些判定三角形相似的方法?
1.定义法:
对应角相等、对应边成比例的两个三角形相似.
2.预备定理:
平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3.(AA)两个角对应相等的两个三角形相似.
类似于判定三角形全等的SSS方法,能不能通过三边对应成比例来判定两个三角形相似呢?
4.(SAS)两边对应成比例且夹角相等,两三角形相似.
新知导入
A
B
C
A′
B′
C′
提示:
能形成A型或X型吗?
(1)在AB边上截取AD=A′B′;
(2)过点D作DE∥BC,交AC于点E;
问:(1)△ADE与△ABC相似吗?
(2)△ADE与△A′B′C′全等吗?
D.
E
所以,△ABC∽△A′B′C′
在△ABC和△A′B′C′中,若
那么△ABC∽△A′B′C′吗?
新知探究
相似三角形的判定定理3
三边对应成比例的两三角形相似。
△ABC∽△A'B'C'.
A'
B'
C'
A
B
C
在△A′B′C'与△ABC中:
例:如图,已知 .不另外添加字母,写出 图中相等的角,并说明理由.
A
C
B
D
E
例:如图,已知 .不另外添加字母,写出 图中相等的角,并说明理由.
A
C
B
D
E
∴∠ABC=∠ADE,∠ACB=∠AED,
∠BAC=∠DAE
∴∠BAD=∠CAE
看已知条件
判定相似
选方法
找够判定方法
中所需的条件
1.下列条件中,能判定△ABC与△DEF相似的有( )
①∠A=45°,AB=12,AC=15,∠D=45°,DE=16,DF=40;
②AB=12,BC=15,AC=24,DE=20,EF=25,DF=40;
③∠A=47°,AB=15,AC=20,∠E=47°,DE=28,EF=21.
A.0个 B.1个
C.2个 D.3个
C
课堂练习
2、图中的两个三角形是否相似?
15
25
20
27
45
40
A
B
C
D
E
45
54
36
30
2、图中的两个三角形是否相似?
15
25
20
27
45
40
A
B
C
D
E
45
54
36
30
∴△ACB∽△ECD
对应边的比不相等
∴图中两个三角形不相似.
对应边的比不相等
A
B
C
D
E
F
3.如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC∽△DEF.
5
12
8
10
A
B
C
D
E
F
3.如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC∽△DEF.
5
12
8
10
16
24
A
B
C
D
E
4.如图,在 △ABC 和 △ADE 中, ,∠BAD=20°,求∠CAE的度数.
∴∠CAE=20°.
A
B
C
D
E
4.如图,在 △ABC 和 △ADE 中, ,∠BAD=20°,求∠CAE的度数.
解:
∴ △ABC ∽△ADE
∴ ∠BAC=∠DAE,
∴∠BAC -∠DAC=∠DAE -∠DAC,
即 ∠BAD=∠CAE.
又∵∠BAD=20°,
∵
判定三角形相似的方法
定义
判定定理1
判定定理2
判定定理3
平行线法
课堂总结
1、课本18练习1,2
2、习题1.2,T2-5
作业布置
A
B
C
O
A′
。
B′
。
C′
。
3、已知:如图,AA′、BB′、CC′相交于点O,且
求证:△ABC∽△A′B′C′
2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
