人教版数学八年级上册14.2.1平方差公式 精品同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级上册14.2.1平方差公式 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-21 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学 14.2.1平方差公式 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.用乘法公式进行简单的计算(a+2b)(a-2b)的结果是
A.a2-4b2 B.a2-2b2 C.a2+4b2 D.-a2+4b2
2.当,时,代数式的值是
A.6 B.8 C.9 D.12
3.计算的结果是
A. B.
C. D.以上答案都不对
4.若a2-b2=4,a-b=1,则a+b的值为
A.-4 B.4 C.1 D.2
5.为了运用平方差公式计算(x+2y-1)(x-2y+1),下列变形正确的是
A.[x-(2y+1)]2 B.[x+(2y-1)][x-(2y-1)]
C.[(x-2y)+1][(x-2y)-1] D.[x+(2y-1)]2
6.用简便方法计算40×39,变形正确的是
A.(40+)(39+) B.(40+)(40-)
C.(40+)(40-) D.(40-)(40-)
7.式子化简的结果为( )
A. B. C. D.
8.可以用平方差公式进行计算的是( ).
A. B.
C. D.
9.根据等式:,,……的规律,则可以推算得出的末位数字是( )
A. B. C. D.
10.···的个位数是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.计算:__________.
12.在一个边长为11.75 cm的正方形纸板内,剪去一个边长为8.25 cm的正方形,剩下部分的面积等于__________cm2.
13.计算=__________.
14.化简______________;
15.已知,,_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.计算.
(1)(0.25x-)(0.25x+0.25);
(2)(x-2y)(-2y-x)-(3x+4y)(-3x+4y);
(3)(2a+b-c-3d)(2a-b-c+3d);
(4)(x-2)(16+x4)(2+x)(4+x2).
17.计算:.
18.如图1所示,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
(1)请问用这两个图可以验证公式法因式分解中的哪个公式?
(2)若图1中的阴影部分的面积是10,a-b=2,求a+b的值;
(3)试利用这个公式计算:
19..如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8dm,r=1.6dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
20.乘法公式的探究及应用.
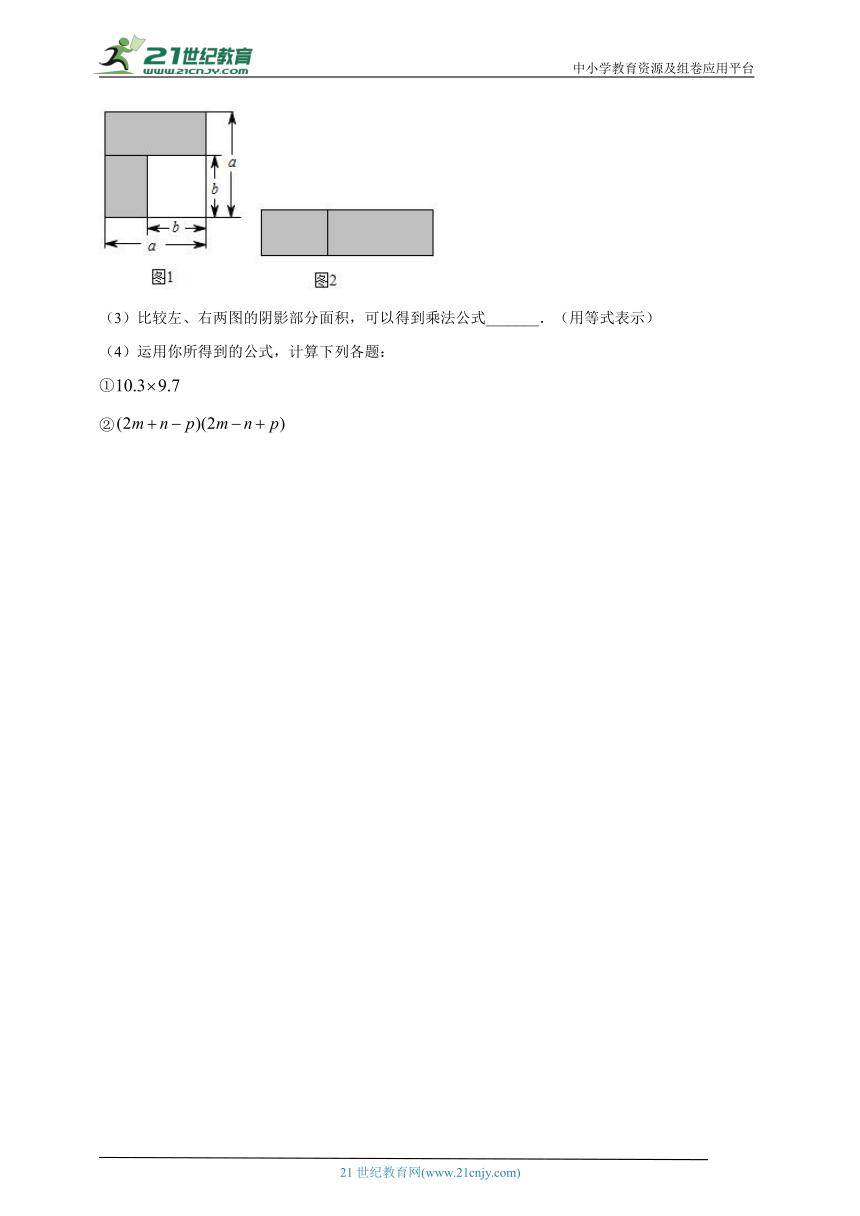
(1)如图1,可以求出阴影部分的面积是_______(写成两数平方差的形式);
(2)图2是将图1中的阴影部分裁剪开,重新拼成的一个长方形,观察它的长和宽,其面积是______(写成多项式乘法的形式).
(3)比较左、右两图的阴影部分面积,可以得到乘法公式_______.(用等式表示)
(4)运用你所得到的公式,计算下列各题:
①
②
参考答案
选择题
1.【答案】A
【解析】(a+2b)(a-2b)=a2-4b2.故选A.
2.【答案】C
【解析】原式=x2-y2+y2=x2,当x=3,y=1时,原式=9.故选C.
3.【答案】A
【解析】(a+1)(a-1)(a2+1)(a4+1)=(a2-1)(a2+1)(a4+1)=(a4-1)(a4+1)=a8-1.故选A.
4.【答案】B
【解析】∵a2-b2=4,a-b=1,由a2-b2=(a+b)(a-b)得到,4=1×(a+b),∴a+b=4,故选B.
5.【答案】B
【解析】(x+2y-1)(x-2y+1)=[x+(2y-1)] [x-(2y-1)],故选B.
6.【答案】B
【解析】运用平方差进行变形为:40×39=(40+)(40-).故选B.
7.【答案】C
【分析】利用添项法,构造平方差公式计算即可.
【详解】设S=,
∴(2—1)S=(2—1)
∴S=
=
=
=,
故选C.
8.【答案】C
【分析】根据两数之和与两数之差的乘积等于两数的平方差判断即可得到正确的选项.
【详解】A.不可用平方差公式,故不符合题意;
B.,不是平方差,故不符合题意;
C.,符合题意;
D.,不是平方差,故不符合题意.
故选C.
9.【答案】B
【分析】利用题目给出的规律:把乘(2-1)得出22022-1,研究22022的末位数字规律,进一步解决问题.
【详解】由题目中等式的规律可得:
=(2-1)×
=22022-1,
21的末位数字是2,22的末位数字是4,23的末位数字是8,24的末位数字是6,25的末位数字是2…,
所以2n的末位数字是以2、4、8、6四个数字一循环.
2022÷4=505…2,
所以22022的末位数字是4,
22022-1的末位数字是3.
故选:B
10.【答案】C
【分析】原式中的3变形为22-1,反复利用平方差公式计算即可得到结果.
【详解】3(22+1)(24+1)(28+1)…(232+1)+1=(22-1)(22+1)(24+1)(28+1)…(232+1)+1
=(24-1)(24+1)(28+1)…(232+1)+1…=264-1+1=264,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵64÷4=16,
∴264个位上数字为6,即原式个位上数字为6.
故选:C.
填空题
11.【答案】1
【解析】根据积的乘方和平方差公式,可把原式变形化简:=.故答案为:1.
12.【答案】70
【解析】剩下部分的面积是11.752-8.252=(11.75+8.25)(11.75-8.25)=20×3.5=70,故答案为:70.
13.【答案】7
【分析】根据平方差公式,得=,计算即可
【详解】∵=
=10×0.7
=7,
故答案为:7.
14.【答案】
【分析】根据乘方的意义以及积的乘方公式的逆运用,结合平方差公式,即可求解.
【详解】原式=
=
=
=
=
=
=,
故答案是:.
15.【答案】;
【分析】根据平方差公式化简,代入求值即可;
【详解】,
∵,,
∴原式;
故答案是.
解答题
16.【解析】(1)原式===.
(2)原式=(-2y+x)(-2y-x)-(4y+3x)(4y-3x)==.
(3)原式=[(2a-c)+(b-3d)][(2a-c)-(b-3d)]=.
(4)原式=(x-2)(x+2)(x2+4)(x4+16)=x8-256.
17.【答案】
【分析】根据整式的混合运算法则进行计算即可求解.
【详解】
.
18.【答案】(1);(2)5;(3)232
【分析】(1)根据两个图形的面积相等,即可写出公式;
(2)根据a2-b2=(a+b)(a-b)=10,把a-b的值代入即可求得a+b的值;
(3)从左到右依次利用平方差公式即可求解.
【详解】(1)平方差公式:
故答案为
(2)∵且,a-b=2∴a+b=5
(3)原式=(2-1)(2+1)(22+1)(24+1)(23+1)(216+1)+1
=(22-1)(22+1)(24+1)(28+1)(216+1)+1
=(24-1)(24+1)(28+1)(216+1)+1
=(28-1)(28+1)(216+1)+1
=(216-1)(216+1)+1
=(232-1)+1
=232
故答案为232
19.【答案】36πdm2
【分析】根据剩余部分的面积=圆形板材的面积﹣四个小圆的面积,即可求解
【详解】根据题意有:剩余部分的面积=圆形板材的面积﹣四个小圆的面积.
剩余部分的面积=πR2﹣4πr2=π(R2﹣4r2)=π(R+2r)(R﹣2r)
将R=6.8dm,r=1.6dm代入上式得:
剩余部分的面积=π(R+2r)(R﹣2r)=π(6.8+3.2)(6.8﹣3.2)=36π.
答:剩余部分的面积为:36π dm2
20.【答案】(1);(2);(3);(4)①99.91;②
【分析】(1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
【详解】(1)利用大正方形面积减去小正方形面积即可求出:,
故填:;
(2)它的宽是a﹣b,长是a+b,面积是,
故填:;
(3)根据题意得出:,
故填:;
(4)①解:原式
;
②解:原式
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级上册数学 14.2.1平方差公式 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.用乘法公式进行简单的计算(a+2b)(a-2b)的结果是
A.a2-4b2 B.a2-2b2 C.a2+4b2 D.-a2+4b2
2.当,时,代数式的值是
A.6 B.8 C.9 D.12
3.计算的结果是
A. B.
C. D.以上答案都不对
4.若a2-b2=4,a-b=1,则a+b的值为
A.-4 B.4 C.1 D.2
5.为了运用平方差公式计算(x+2y-1)(x-2y+1),下列变形正确的是
A.[x-(2y+1)]2 B.[x+(2y-1)][x-(2y-1)]
C.[(x-2y)+1][(x-2y)-1] D.[x+(2y-1)]2
6.用简便方法计算40×39,变形正确的是
A.(40+)(39+) B.(40+)(40-)
C.(40+)(40-) D.(40-)(40-)
7.式子化简的结果为( )
A. B. C. D.
8.可以用平方差公式进行计算的是( ).
A. B.
C. D.
9.根据等式:,,……的规律,则可以推算得出的末位数字是( )
A. B. C. D.
10.···的个位数是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.计算:__________.
12.在一个边长为11.75 cm的正方形纸板内,剪去一个边长为8.25 cm的正方形,剩下部分的面积等于__________cm2.
13.计算=__________.
14.化简______________;
15.已知,,_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.计算.
(1)(0.25x-)(0.25x+0.25);
(2)(x-2y)(-2y-x)-(3x+4y)(-3x+4y);
(3)(2a+b-c-3d)(2a-b-c+3d);
(4)(x-2)(16+x4)(2+x)(4+x2).
17.计算:.
18.如图1所示,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
(1)请问用这两个图可以验证公式法因式分解中的哪个公式?
(2)若图1中的阴影部分的面积是10,a-b=2,求a+b的值;
(3)试利用这个公式计算:
19..如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8dm,r=1.6dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
20.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是_______(写成两数平方差的形式);
(2)图2是将图1中的阴影部分裁剪开,重新拼成的一个长方形,观察它的长和宽,其面积是______(写成多项式乘法的形式).
(3)比较左、右两图的阴影部分面积,可以得到乘法公式_______.(用等式表示)
(4)运用你所得到的公式,计算下列各题:
①
②
参考答案
选择题
1.【答案】A
【解析】(a+2b)(a-2b)=a2-4b2.故选A.
2.【答案】C
【解析】原式=x2-y2+y2=x2,当x=3,y=1时,原式=9.故选C.
3.【答案】A
【解析】(a+1)(a-1)(a2+1)(a4+1)=(a2-1)(a2+1)(a4+1)=(a4-1)(a4+1)=a8-1.故选A.
4.【答案】B
【解析】∵a2-b2=4,a-b=1,由a2-b2=(a+b)(a-b)得到,4=1×(a+b),∴a+b=4,故选B.
5.【答案】B
【解析】(x+2y-1)(x-2y+1)=[x+(2y-1)] [x-(2y-1)],故选B.
6.【答案】B
【解析】运用平方差进行变形为:40×39=(40+)(40-).故选B.
7.【答案】C
【分析】利用添项法,构造平方差公式计算即可.
【详解】设S=,
∴(2—1)S=(2—1)
∴S=
=
=
=,
故选C.
8.【答案】C
【分析】根据两数之和与两数之差的乘积等于两数的平方差判断即可得到正确的选项.
【详解】A.不可用平方差公式,故不符合题意;
B.,不是平方差,故不符合题意;
C.,符合题意;
D.,不是平方差,故不符合题意.
故选C.
9.【答案】B
【分析】利用题目给出的规律:把乘(2-1)得出22022-1,研究22022的末位数字规律,进一步解决问题.
【详解】由题目中等式的规律可得:
=(2-1)×
=22022-1,
21的末位数字是2,22的末位数字是4,23的末位数字是8,24的末位数字是6,25的末位数字是2…,
所以2n的末位数字是以2、4、8、6四个数字一循环.
2022÷4=505…2,
所以22022的末位数字是4,
22022-1的末位数字是3.
故选:B
10.【答案】C
【分析】原式中的3变形为22-1,反复利用平方差公式计算即可得到结果.
【详解】3(22+1)(24+1)(28+1)…(232+1)+1=(22-1)(22+1)(24+1)(28+1)…(232+1)+1
=(24-1)(24+1)(28+1)…(232+1)+1…=264-1+1=264,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵64÷4=16,
∴264个位上数字为6,即原式个位上数字为6.
故选:C.
填空题
11.【答案】1
【解析】根据积的乘方和平方差公式,可把原式变形化简:=.故答案为:1.
12.【答案】70
【解析】剩下部分的面积是11.752-8.252=(11.75+8.25)(11.75-8.25)=20×3.5=70,故答案为:70.
13.【答案】7
【分析】根据平方差公式,得=,计算即可
【详解】∵=
=10×0.7
=7,
故答案为:7.
14.【答案】
【分析】根据乘方的意义以及积的乘方公式的逆运用,结合平方差公式,即可求解.
【详解】原式=
=
=
=
=
=
=,
故答案是:.
15.【答案】;
【分析】根据平方差公式化简,代入求值即可;
【详解】,
∵,,
∴原式;
故答案是.
解答题
16.【解析】(1)原式===.
(2)原式=(-2y+x)(-2y-x)-(4y+3x)(4y-3x)==.
(3)原式=[(2a-c)+(b-3d)][(2a-c)-(b-3d)]=.
(4)原式=(x-2)(x+2)(x2+4)(x4+16)=x8-256.
17.【答案】
【分析】根据整式的混合运算法则进行计算即可求解.
【详解】
.
18.【答案】(1);(2)5;(3)232
【分析】(1)根据两个图形的面积相等,即可写出公式;
(2)根据a2-b2=(a+b)(a-b)=10,把a-b的值代入即可求得a+b的值;
(3)从左到右依次利用平方差公式即可求解.
【详解】(1)平方差公式:
故答案为
(2)∵且,a-b=2∴a+b=5
(3)原式=(2-1)(2+1)(22+1)(24+1)(23+1)(216+1)+1
=(22-1)(22+1)(24+1)(28+1)(216+1)+1
=(24-1)(24+1)(28+1)(216+1)+1
=(28-1)(28+1)(216+1)+1
=(216-1)(216+1)+1
=(232-1)+1
=232
故答案为232
19.【答案】36πdm2
【分析】根据剩余部分的面积=圆形板材的面积﹣四个小圆的面积,即可求解
【详解】根据题意有:剩余部分的面积=圆形板材的面积﹣四个小圆的面积.
剩余部分的面积=πR2﹣4πr2=π(R2﹣4r2)=π(R+2r)(R﹣2r)
将R=6.8dm,r=1.6dm代入上式得:
剩余部分的面积=π(R+2r)(R﹣2r)=π(6.8+3.2)(6.8﹣3.2)=36π.
答:剩余部分的面积为:36π dm2
20.【答案】(1);(2);(3);(4)①99.91;②
【分析】(1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
【详解】(1)利用大正方形面积减去小正方形面积即可求出:,
故填:;
(2)它的宽是a﹣b,长是a+b,面积是,
故填:;
(3)根据题意得出:,
故填:;
(4)①解:原式
;
②解:原式
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
