2024年秋华师大版七年级数学上册1.10 有理数的除法 课件(共21张PPT)
文档属性
| 名称 | 2024年秋华师大版七年级数学上册1.10 有理数的除法 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 801.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 10:46:23 | ||
图片预览








文档简介
(共21张PPT)
华师大版 七年级 上册
1.10 有理数的除法
复习导入
有理数的乘法法则是什么?
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与0相乘,都得零.
两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘,都得 0 .
1.小学里已经学过数的除法.回想一下,除法的意义
是什么?它与乘法有什么关系?
已知两个数的积和一个乘数,求另一个乘数.
除法与乘法是互逆运算关系.
2.小学学习过的倒数的意义是什么?
如果两个数的积为1,那么这两个数互为倒数,用式子表示为:
注意:0 没有倒数哟!
如果一个数与 2 的乘积是﹣6 ,那么这个数是几?
探究新知
乘法算式:__________________
除法算式:__________________
2×( )=﹣6
(﹣6)÷2=( )
3
﹣3
另外,我们还知道
(﹣6)× =﹣3
比较以上两式,即有
(﹣6)÷2=(﹣6)×
这表明,除法可以转化为乘法来进行运算.
﹣
倒数
负数也有倒数吗?
例如, 互为倒数, 互为倒数.
小学里我们学过倒数,对于有理数仍然有:
乘积是 1 的两个数互为倒数.
你能再举出几个互为倒数的有理数吗?
正
由于“两数相乘,同号得正”,所以互为倒数的两个数正负号相同.
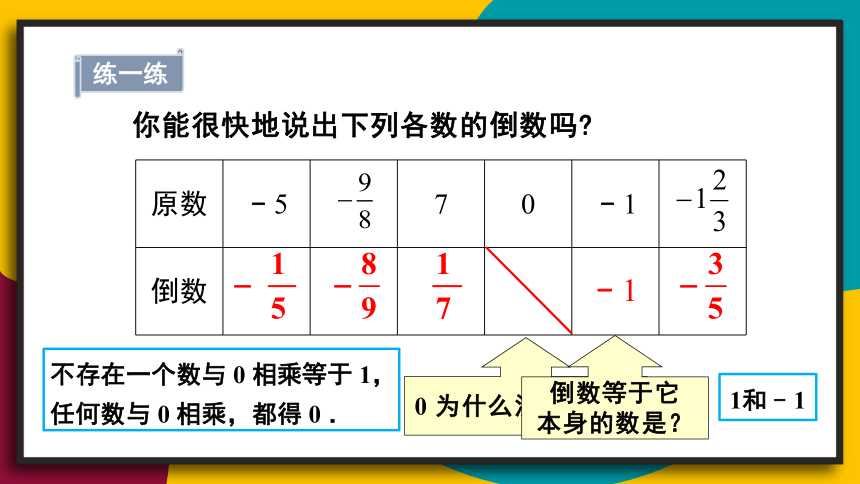
你能很快地说出下列各数的倒数吗
原数 ﹣5 7 0 ﹣1
倒数
﹣1
0 为什么没有倒数?
练一练
不存在一个数与 0 相乘等于 1,任何数与 0 相乘,都得 0 .
倒数等于它
本身的数是?
1和﹣1
倒数的求法:
相反数 倒数
定义
表示(原数为a)
找对应数的方法
正负 关系 正数
负数
0
等于自身的数
﹣a
仅有符号不同的两数
乘积为 1 的两数
改变该数的正负号
颠倒分子、分母的位置
(小数化为分数)
负数
负数
正数
正数
0
0
无
1,﹣1
4
-3
-25
3
0
4
-3
3
-25
0
已知积和其中一个因数,
求另一个因数
积÷因数=另一个因数
除法是乘法的逆运算
填空
有理数的除法可以转化为乘法:
除以一个数等于乘以这个数的倒数.
0 不能作除数.
注意
为什么?
因为 0 没有倒数.
除法变为乘法
除数变为其倒数
(其他式子同理)
计算:
(1) (-18)÷6;
(2) ;
(3) .
(1) (-18)÷6=(-18)× =-3.
例1
解
示例:
因为除法可以转化为乘法,所以与乘法类似,我们也有如下有理数的除法法则:
两数相除,同号得正,异号得负,并把绝对值相除.
0 除以任何一个不等于 0 的数,都得 0 .
有理数都可以表示成两个整数之商.
(有理数的本质)
有理数的本质:
有理数就是可以表示成两个整数之商的数.
有理数
整数
正分数
负分数
分数
任何整数都是它除以 1 所得的商
(带分数先化成假分数)
分子除以分母所得的商
负号放到分子或分母上
两个整数(其中一个为负整数)的商
例如, ,它是﹣22 与 7 或 22 与﹣7 的商.
化简下列分数:
例2
解
计算:
例3
解
巩固练习
1.写出下列各数的倒数:
(1) ; (2) ; (3)﹣5; (4)1; (5)﹣1; (6)0.2.
【教材P52 练习 第1题】
=﹣12
=﹣4
= 0
=﹣40
【教材P52 练习 第2题】
2.计算:
不正确,此题应按从左到右的顺序计算,正确的是:
【教材P53 练习 第3题】
3.下列计算正确吗?为什么?
课堂小结
有理数的除法可以转化为乘法:
除以一个数等于乘以这个数的倒数.0 不能作除数.
有理数的除法法则:
两数相除,同号得正,异号得负,并把绝对值相除.
0 除以任何一个不等于 0 的数,都得 0 .
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华师大版 七年级 上册
1.10 有理数的除法
复习导入
有理数的乘法法则是什么?
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与0相乘,都得零.
两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘,都得 0 .
1.小学里已经学过数的除法.回想一下,除法的意义
是什么?它与乘法有什么关系?
已知两个数的积和一个乘数,求另一个乘数.
除法与乘法是互逆运算关系.
2.小学学习过的倒数的意义是什么?
如果两个数的积为1,那么这两个数互为倒数,用式子表示为:
注意:0 没有倒数哟!
如果一个数与 2 的乘积是﹣6 ,那么这个数是几?
探究新知
乘法算式:__________________
除法算式:__________________
2×( )=﹣6
(﹣6)÷2=( )
3
﹣3
另外,我们还知道
(﹣6)× =﹣3
比较以上两式,即有
(﹣6)÷2=(﹣6)×
这表明,除法可以转化为乘法来进行运算.
﹣
倒数
负数也有倒数吗?
例如, 互为倒数, 互为倒数.
小学里我们学过倒数,对于有理数仍然有:
乘积是 1 的两个数互为倒数.
你能再举出几个互为倒数的有理数吗?
正
由于“两数相乘,同号得正”,所以互为倒数的两个数正负号相同.
你能很快地说出下列各数的倒数吗
原数 ﹣5 7 0 ﹣1
倒数
﹣1
0 为什么没有倒数?
练一练
不存在一个数与 0 相乘等于 1,任何数与 0 相乘,都得 0 .
倒数等于它
本身的数是?
1和﹣1
倒数的求法:
相反数 倒数
定义
表示(原数为a)
找对应数的方法
正负 关系 正数
负数
0
等于自身的数
﹣a
仅有符号不同的两数
乘积为 1 的两数
改变该数的正负号
颠倒分子、分母的位置
(小数化为分数)
负数
负数
正数
正数
0
0
无
1,﹣1
4
-3
-25
3
0
4
-3
3
-25
0
已知积和其中一个因数,
求另一个因数
积÷因数=另一个因数
除法是乘法的逆运算
填空
有理数的除法可以转化为乘法:
除以一个数等于乘以这个数的倒数.
0 不能作除数.
注意
为什么?
因为 0 没有倒数.
除法变为乘法
除数变为其倒数
(其他式子同理)
计算:
(1) (-18)÷6;
(2) ;
(3) .
(1) (-18)÷6=(-18)× =-3.
例1
解
示例:
因为除法可以转化为乘法,所以与乘法类似,我们也有如下有理数的除法法则:
两数相除,同号得正,异号得负,并把绝对值相除.
0 除以任何一个不等于 0 的数,都得 0 .
有理数都可以表示成两个整数之商.
(有理数的本质)
有理数的本质:
有理数就是可以表示成两个整数之商的数.
有理数
整数
正分数
负分数
分数
任何整数都是它除以 1 所得的商
(带分数先化成假分数)
分子除以分母所得的商
负号放到分子或分母上
两个整数(其中一个为负整数)的商
例如, ,它是﹣22 与 7 或 22 与﹣7 的商.
化简下列分数:
例2
解
计算:
例3
解
巩固练习
1.写出下列各数的倒数:
(1) ; (2) ; (3)﹣5; (4)1; (5)﹣1; (6)0.2.
【教材P52 练习 第1题】
=﹣12
=﹣4
= 0
=﹣40
【教材P52 练习 第2题】
2.计算:
不正确,此题应按从左到右的顺序计算,正确的是:
【教材P53 练习 第3题】
3.下列计算正确吗?为什么?
课堂小结
有理数的除法可以转化为乘法:
除以一个数等于乘以这个数的倒数.0 不能作除数.
有理数的除法法则:
两数相除,同号得正,异号得负,并把绝对值相除.
0 除以任何一个不等于 0 的数,都得 0 .
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
