2024年秋华师大版七年级数学上册1.11.1 有理数的乘方 课件(共18张PPT)
文档属性
| 名称 | 2024年秋华师大版七年级数学上册1.11.1 有理数的乘方 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 606.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 10:46:58 | ||
图片预览





文档简介
(共18张PPT)
华师大版 七年级 上册
1.11 有理数的乘方
第 1 课时 有理数的乘方
情境导入
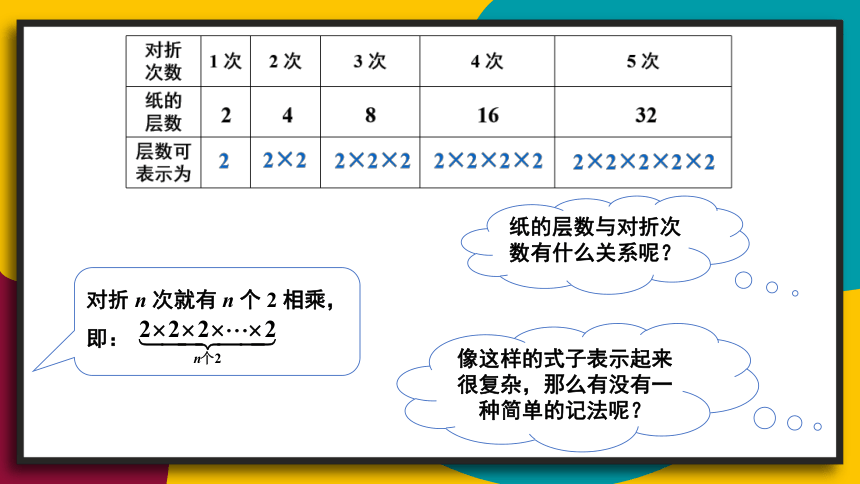
请同学们拿出一张纸进行对折,再对折……两人合作,一人对折,一人记录下表:
对折 次数 1 次 2 次 3 次 4 次 5 次
纸的 层数
层数可 表示为
2
4
8
16
32
2×2
2×2×2
2×2×2×2
2×2×2×2×2
2
…
纸的层数与对折次数有什么关系呢?
对折 n 次就有 n 个 2 相乘,即:
像这样的式子表示起来很复杂,那么有没有一种简单的记法呢?
探究新知
边长为 a cm 的正方形的面积为______cm2.
棱长为 a cm 的正方体的体积为______cm3.
a
a
a×a
a×a×a
读作: a 的平方(或 a 的 2 次方)
读作: a 的立方(或 a 的 3 次方)
a·a 记作 ,读作 a 的平方(或 a 的 2 次方);
a·a·a 记作 ,读作 a 的立方(或 a 的 3 次方).
记作
一般地,n 个相同的乘数 a 相乘:
记作 ,
读作 a 的 n 次方
n个
a·a·…·a
a·a·…·a
n个
这种求几个相同乘数的积的运算,叫做乘方,乘方的结果叫做幂.
当把 看作是 a 的 n 次方的结果时, 也可读作 a 的 n 次幂.
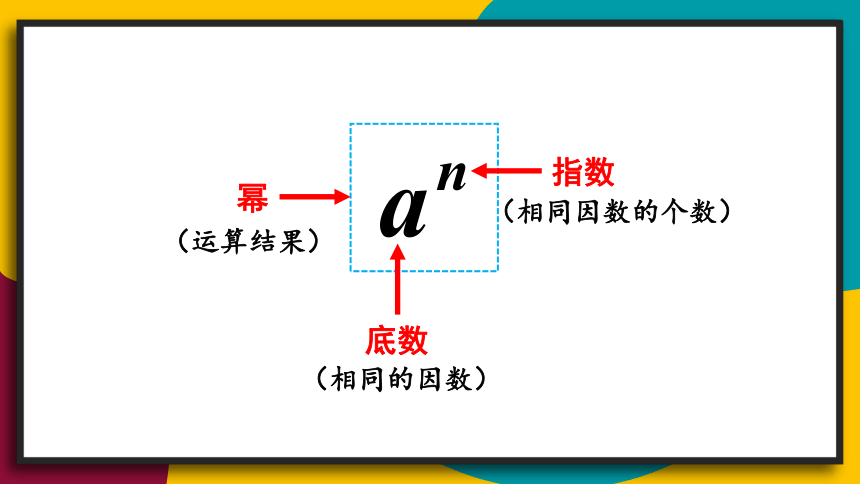
(相同的因数)
(相同因数的个数)
(运算结果)
底数
指数
幂
1.在 中,底数是_____,指数是_____,表示的意义是___________.
2.在 中,底数是_____,指数是_____,表示的意义是___________.
3.在 中,底数是_____,指数是_____,表示的意义是___________.
3个 相乘
4个﹣3相乘
5
2
2个5相乘
﹣3
4
3
在 8 中,底数是_____,指数是_____.
8
1
一个数可以看作这个数本身的 1 次方, 就是 a,指数 1 通常省略不写.
计算:
(1) ;
(2) ;
(3) .
(1)(-2)3=(-2)(-2)(-2)
(2)(-2)4=(-2)(-2)(-2)(-2)
(3)(-2)5=(-2)(-2)(-2)(-2)(-2)
例1
解
=-8.
=16.
=-32.
(-2)3
(-2)4
(-2)5
乘方运算的步骤:
转化
乘方运算
乘法运算
① 确定幂的符号
② 计算幂的绝对值
不相同,括号不能省!
=-8.
=16.
=-32.
(-2)3
(-2)4
(-2)5
观察上述结果的正负号,你发现了什么?
8
16
32
根据有理数的乘法法则,我们有:
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
0 的任何正整数次幂都是 0 .
根据任何数与 0 相乘,都得 0 ,可以得出:
1 的任何次幂都是 .
﹣1 的偶次幂是 ,奇次幂是 .
1
﹣1
1
任何数的
偶次幂都
是非负数
你能迅速判断下列各幂的正负吗?
+
+
-
+
-
+
+
+
0
+
+
两个重要的非负数:
巩固练习
1. 读作什么?其中底数是什么?指数
是什么? 是正数还是负数?
读作负 4 的 5 次方,底数是﹣4,指数是 5,它是负数.
【教材P55 练习 第1题】
=1000
=100000
=﹣1
=1
=﹣0.001
=﹣32
2.计算:
【教材P55 练习 第2题】
3.3 的平方是什么?﹣3 的平方是什么?平方得 9 的
数有几个?有没有平方得﹣9 的有理数?
【教材P55 练习 第3题】
是 9, 是 9,平方得 9 的数有两个,没有平方得﹣9 的有理数.
课堂小结
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华师大版 七年级 上册
1.11 有理数的乘方
第 1 课时 有理数的乘方
情境导入
请同学们拿出一张纸进行对折,再对折……两人合作,一人对折,一人记录下表:
对折 次数 1 次 2 次 3 次 4 次 5 次
纸的 层数
层数可 表示为
2
4
8
16
32
2×2
2×2×2
2×2×2×2
2×2×2×2×2
2
…
纸的层数与对折次数有什么关系呢?
对折 n 次就有 n 个 2 相乘,即:
像这样的式子表示起来很复杂,那么有没有一种简单的记法呢?
探究新知
边长为 a cm 的正方形的面积为______cm2.
棱长为 a cm 的正方体的体积为______cm3.
a
a
a×a
a×a×a
读作: a 的平方(或 a 的 2 次方)
读作: a 的立方(或 a 的 3 次方)
a·a 记作 ,读作 a 的平方(或 a 的 2 次方);
a·a·a 记作 ,读作 a 的立方(或 a 的 3 次方).
记作
一般地,n 个相同的乘数 a 相乘:
记作 ,
读作 a 的 n 次方
n个
a·a·…·a
a·a·…·a
n个
这种求几个相同乘数的积的运算,叫做乘方,乘方的结果叫做幂.
当把 看作是 a 的 n 次方的结果时, 也可读作 a 的 n 次幂.
(相同的因数)
(相同因数的个数)
(运算结果)
底数
指数
幂
1.在 中,底数是_____,指数是_____,表示的意义是___________.
2.在 中,底数是_____,指数是_____,表示的意义是___________.
3.在 中,底数是_____,指数是_____,表示的意义是___________.
3个 相乘
4个﹣3相乘
5
2
2个5相乘
﹣3
4
3
在 8 中,底数是_____,指数是_____.
8
1
一个数可以看作这个数本身的 1 次方, 就是 a,指数 1 通常省略不写.
计算:
(1) ;
(2) ;
(3) .
(1)(-2)3=(-2)(-2)(-2)
(2)(-2)4=(-2)(-2)(-2)(-2)
(3)(-2)5=(-2)(-2)(-2)(-2)(-2)
例1
解
=-8.
=16.
=-32.
(-2)3
(-2)4
(-2)5
乘方运算的步骤:
转化
乘方运算
乘法运算
① 确定幂的符号
② 计算幂的绝对值
不相同,括号不能省!
=-8.
=16.
=-32.
(-2)3
(-2)4
(-2)5
观察上述结果的正负号,你发现了什么?
8
16
32
根据有理数的乘法法则,我们有:
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
0 的任何正整数次幂都是 0 .
根据任何数与 0 相乘,都得 0 ,可以得出:
1 的任何次幂都是 .
﹣1 的偶次幂是 ,奇次幂是 .
1
﹣1
1
任何数的
偶次幂都
是非负数
你能迅速判断下列各幂的正负吗?
+
+
-
+
-
+
+
+
0
+
+
两个重要的非负数:
巩固练习
1. 读作什么?其中底数是什么?指数
是什么? 是正数还是负数?
读作负 4 的 5 次方,底数是﹣4,指数是 5,它是负数.
【教材P55 练习 第1题】
=1000
=100000
=﹣1
=1
=﹣0.001
=﹣32
2.计算:
【教材P55 练习 第2题】
3.3 的平方是什么?﹣3 的平方是什么?平方得 9 的
数有几个?有没有平方得﹣9 的有理数?
【教材P55 练习 第3题】
是 9, 是 9,平方得 9 的数有两个,没有平方得﹣9 的有理数.
课堂小结
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
同课章节目录
