1.1.2 有理数课件(13张PPT)2024年秋华师大版七年级数学上册
文档属性
| 名称 | 1.1.2 有理数课件(13张PPT)2024年秋华师大版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 831.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-22 19:35:54 | ||
图片预览



文档简介
(共13张PPT)
华师大版 七年级 上册
1.1 有理数的引入
有理数
02
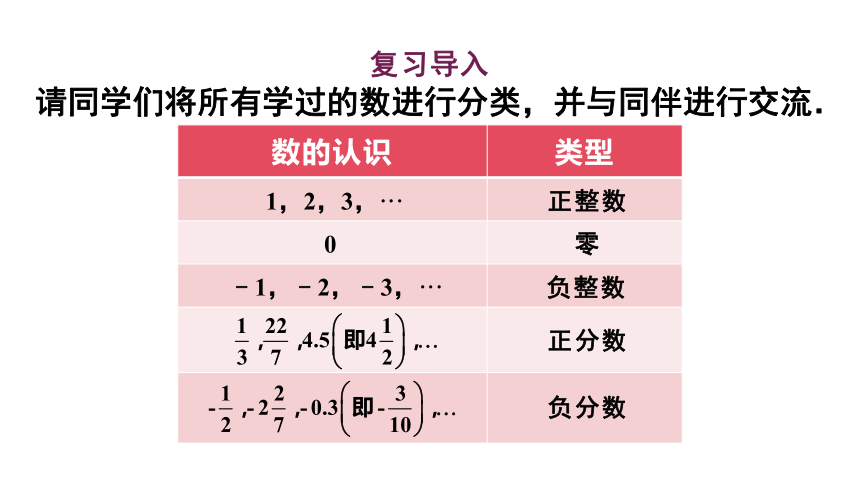
复习导入
请同学们将所有学过的数进行分类,并与同伴进行交流.
数的认识 类型
1,2,3,···
正整数
0
零
﹣1,﹣2,﹣3,···
负整数
正分数
负分数
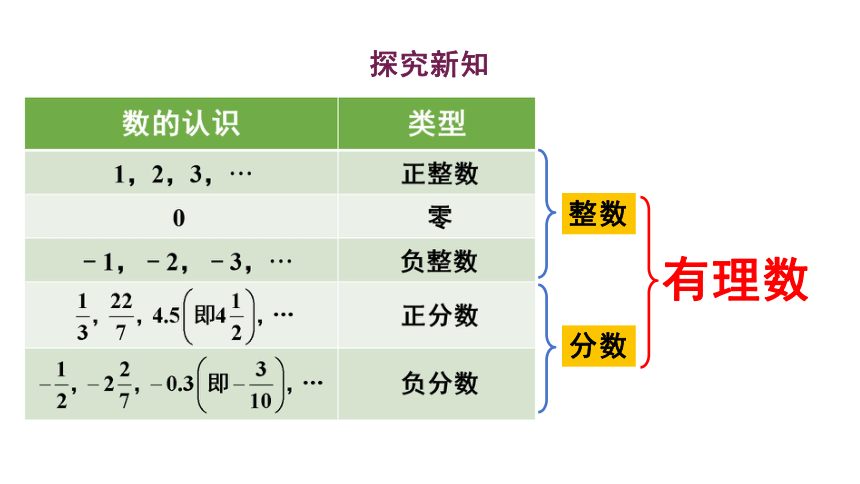
探究新知
整数
分数
有理数
整数和分数统称为有理数.
有理数的定义
“有理数”的英文名 rational number 中的单词 rational 应看成 ratio(比、比率)的形容词形式.因此,rational number 应该理解为“比率数”,即可以表示为两个整数之商(比率)的数.在学习了有理数的除法(1.10节)之后我们可以看到,这样的解释准确地描述了有理数的本质.
为什么叫“有理数”?
有理数
整数
正整数
0
负整数
正分数
负分数
分数
有理数
正有理数
正整数
0
负整数
正分数
负分数
负有理数
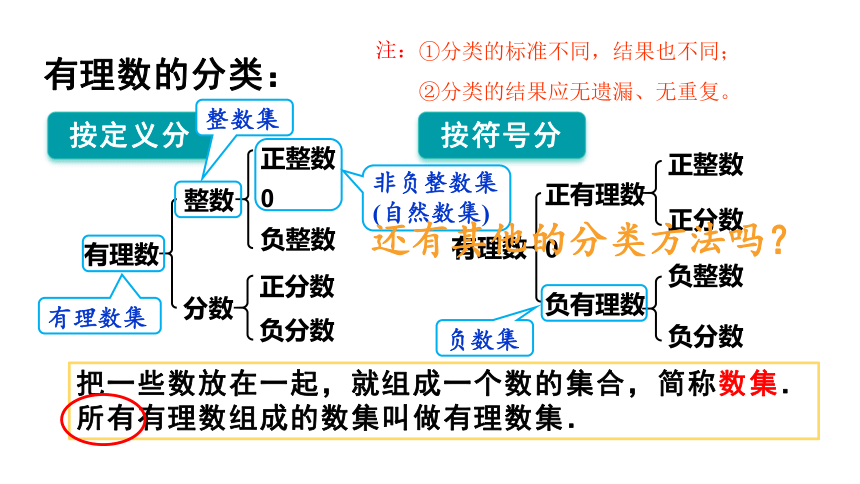
按定义分
按符号分
整数集
有理数集
负数集
非负整数集
(自然数集)
有理数的分类:
还有其他的分类方法吗?
①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复。
注:
把一些数放在一起,就组成一个数的集合,简称数集.
所有有理数组成的数集叫做有理数集.
正数集
负数集
整数集
有理数集
例1
把下列各数填入表示它们所在的数集的圈里:
﹣18, 3.1416,0,2023, ﹣0.142857,95%.
都是
3.1416,
2023,
95%
﹣18,
﹣0.142857
﹣18,
0,
2023
正数 负数 整数 分数 有理数
-8
0.9
0
π
例2
判断表中各数分别是什么数,在相应的空格中打√.
π不是有理数.
(1)0是整数;( ) (6)所有的整数都是正数;( )
(2)自然数一定是整数;( ) (7)所有的正数都是整数;( )
(3)0是正整数;( ) (8)一个数不是正数就是负数;( )
(4)整数一定是自然数;( ) (9)分数一定是有理数;( )
(5)任何小数都是有理数;( ) (10)0是最小的有理数.( )
例3
判断下列说法是否正确.
非负整数
无限不循环小数
0
巩固练习
1.请说出两个正整数、两个负整数、两个正
分数、两个负分数.它们都是有理数吗?
【教材P6 练习 第1题】
解:(答案不唯一)两个正整数:1,2:
两个负整数:-2,-7;
两个正分数:
两个负分数:
它们都是有理数.
2.有理数集中有没有这样的数,它既不是正数,
也不是负数?若有,请说出这样的数.
解:有,它是 0.
【教材P6 练习 第2题】
有理数按照不同的标准可以分为哪几类?
课堂小结
有理数
整数
正整数
0
负整数
正分数
负分数
分数
或
有理数
正有理数
正整数
0
负整数
正分数
负分数
负有理数
按定义分
按符号分
整数与分数统称为有理数.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
华师大版 七年级 上册
1.1 有理数的引入
有理数
02
复习导入
请同学们将所有学过的数进行分类,并与同伴进行交流.
数的认识 类型
1,2,3,···
正整数
0
零
﹣1,﹣2,﹣3,···
负整数
正分数
负分数
探究新知
整数
分数
有理数
整数和分数统称为有理数.
有理数的定义
“有理数”的英文名 rational number 中的单词 rational 应看成 ratio(比、比率)的形容词形式.因此,rational number 应该理解为“比率数”,即可以表示为两个整数之商(比率)的数.在学习了有理数的除法(1.10节)之后我们可以看到,这样的解释准确地描述了有理数的本质.
为什么叫“有理数”?
有理数
整数
正整数
0
负整数
正分数
负分数
分数
有理数
正有理数
正整数
0
负整数
正分数
负分数
负有理数
按定义分
按符号分
整数集
有理数集
负数集
非负整数集
(自然数集)
有理数的分类:
还有其他的分类方法吗?
①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复。
注:
把一些数放在一起,就组成一个数的集合,简称数集.
所有有理数组成的数集叫做有理数集.
正数集
负数集
整数集
有理数集
例1
把下列各数填入表示它们所在的数集的圈里:
﹣18, 3.1416,0,2023, ﹣0.142857,95%.
都是
3.1416,
2023,
95%
﹣18,
﹣0.142857
﹣18,
0,
2023
正数 负数 整数 分数 有理数
-8
0.9
0
π
例2
判断表中各数分别是什么数,在相应的空格中打√.
π不是有理数.
(1)0是整数;( ) (6)所有的整数都是正数;( )
(2)自然数一定是整数;( ) (7)所有的正数都是整数;( )
(3)0是正整数;( ) (8)一个数不是正数就是负数;( )
(4)整数一定是自然数;( ) (9)分数一定是有理数;( )
(5)任何小数都是有理数;( ) (10)0是最小的有理数.( )
例3
判断下列说法是否正确.
非负整数
无限不循环小数
0
巩固练习
1.请说出两个正整数、两个负整数、两个正
分数、两个负分数.它们都是有理数吗?
【教材P6 练习 第1题】
解:(答案不唯一)两个正整数:1,2:
两个负整数:-2,-7;
两个正分数:
两个负分数:
它们都是有理数.
2.有理数集中有没有这样的数,它既不是正数,
也不是负数?若有,请说出这样的数.
解:有,它是 0.
【教材P6 练习 第2题】
有理数按照不同的标准可以分为哪几类?
课堂小结
有理数
整数
正整数
0
负整数
正分数
负分数
分数
或
有理数
正有理数
正整数
0
负整数
正分数
负分数
负有理数
按定义分
按符号分
整数与分数统称为有理数.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
