4.4可能性大小的应用(教学课件)(共23张PPT)-五年级数学上册(人教版)
文档属性
| 名称 | 4.4可能性大小的应用(教学课件)(共23张PPT)-五年级数学上册(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-23 09:58:21 | ||
图片预览






文档简介
(共23张PPT)
第4课时 可能性大小的应用
小学数学·五年级(上)·人教版
1. 进一步体会不确定现象的特点及事件发生的可能性的大小。
2. 经历事件发生的可能性大小的探索过程,能根据试验的统计结果进行判断和推测,知道事件发生的可能性的大小与物体数量的多少有关,进一步体会随机现象的统计规律性,能根据数据推测事件发生的可能性的大小。
3. 进一步培养求实态度和科学精神。
【重点】
进一步体会随机现象的统计规律性,能根据数据推测事件发生的可能性的大小。
【难点】
理解随机现象和统计规律之间的关系。
回顾交流:
一叠扑克牌中有12张红桃、6张黑桃和3张梅花。摸出哪种花色牌的可能性最大?为什么?
可能性最大
最多
小组活动:在装有红、黄两种颜色小球的盒子里摸球,每个小组的盒子里装的球都一样。每次摸出一个球,记录下颜色,再放回去摇匀,重复20次。
小组合作:记录从盒中摸20次的结果。
合作要求
1. 小组成员分工合作。
2. 每次摸球前要将盒子里的球摇匀。
3. 每次摸出一个球,再放回去,重复20次。
4. 每摸出一个球后记录下它的颜色,可以用画“正”字的方法来记录。
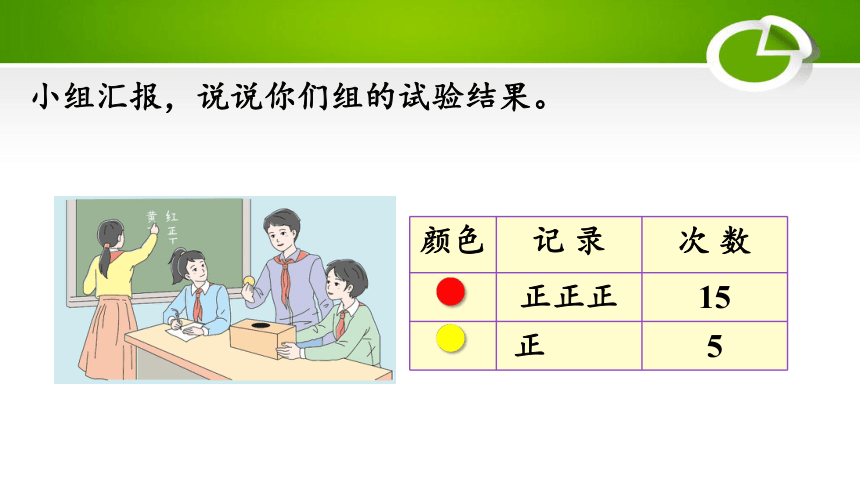
小组汇报,说说你们组的试验结果。
颜色 记 录 次 数
正正正 15
正 5
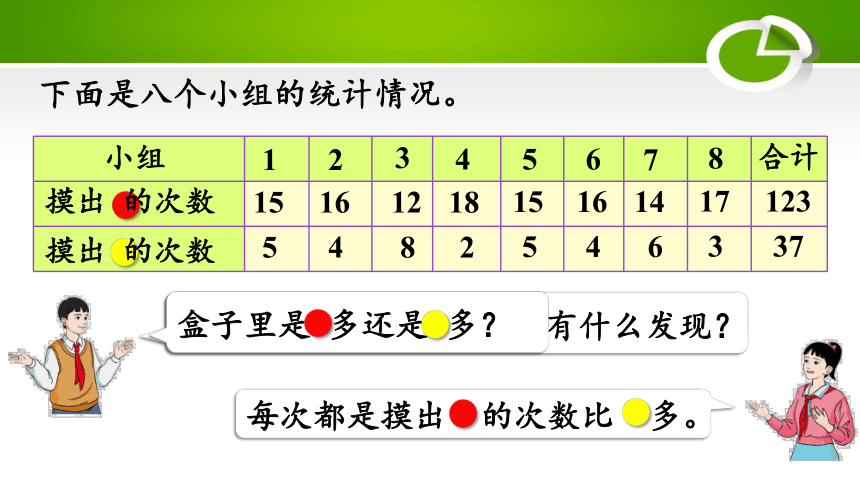
下面是八个小组的统计情况。
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
仔细观察上面的表格,你有什么发现?
每次都是摸出 的次数比 多。
盒子里是 多还是 多?
小组
摸出 的次数
摸出 的次数
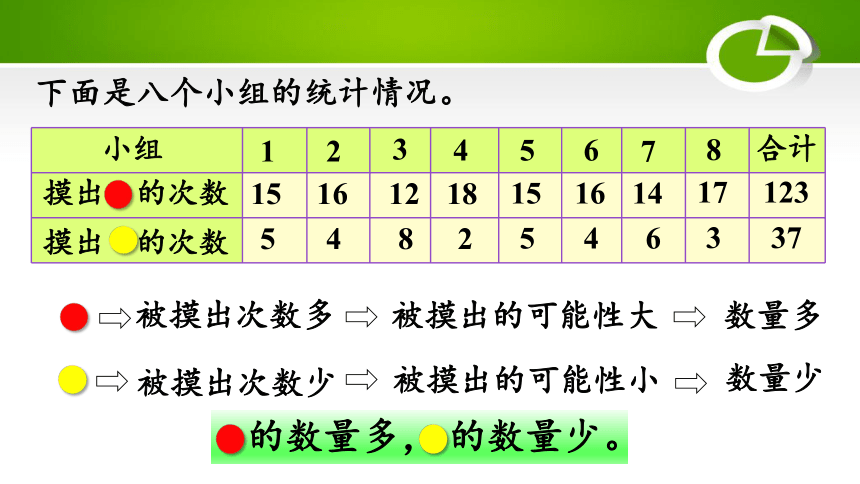
下面是八个小组的统计情况。
被摸出次数多
被摸出的可能性大
数量多
被摸出次数少
被摸出的可能性小
数量少
的数量多, 的数量少。
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
小组
摸出 的次数
摸出 的次数
真的是这样吗?让我们来验证一下吧。
下面是八个小组的统计情况。
哇,盒子里果然是 多。
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
小组
摸出 的次数
摸出 的次数
由以上试验可知,事件发生的可能性的大小能反映出个体的数量的多少:
可能性越大,个体在总数中所占数量越多; 可能性越小,个体在总数中所占数量越少。
思考:
(1)如果再摸一次,摸出哪种颜色的球的可能性大?
(2)如果继续摸下去,结果是不是一定摸出红色球?
(3)如果要使摸出的黄球的可能性大,可以怎么办?
从盒子里摸出一个棋子,可能是蓝色、黄色或红色。
1. 从下面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
因为盒子里红色棋子最多,黄色棋子最少,所以摸出红色棋子的可能性最大,摸出黄色棋子的可能性最小。
1. 从下面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
2.
全班每人掷一次。
掷出 朝上的有___人,
掷出 朝上的有___人。
哪面朝上?
朝上的可能性大还是 朝上的可能性大?
两面朝上的可能性应该是相等的。可为什么出现一个多一个少的现象呢?
如果有更多的人来掷,结果会怎样呢?
5红面1蓝面, 4红面2蓝面。
3. 给 涂上红、蓝两种颜色,要使掷出红色面朝上的可能性比蓝色面大,应该怎么涂?
红色面应比蓝色面多。
或5红1蓝。
所以可以涂 4红2蓝
共6个面
1.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上的数字应该怎样填?请你填一填。
1
1
1
1
1
1
1
1
5
卡片中 “1”的张数要最多;
卡片中 “5”的张数要最少。
1
1
1
1
1
1
1
1
1
5
5
1
1
1
1
1
1
1
2
2
5
1
1
1
1
1
1
4
4
4
5
10张卡片中可以只有“1”和“5”两个数字,也可以有其他数字。
1.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上可以是什么数字?请你填一填。
(1)
(2)
2. 小宇要设计一个转盘,上面画着 和 两种图案。如果要达到下面的要求,他该怎么画?
(1)任意转动1次,转到 的可能性大。
(2)任意转动1次,一定转到 。
的数量要多
都是
(答案不唯一)
(3)
(4)
(3)任意转动1次,转到 和 的可能性一样大。
(4)任意转到1次,不可能转到 。
和 的数量一样多
只有 ,没有
3. 小亮和小强玩摸球游戏(盒子里的球如右图所示)。一次摸 2个球,摸后放回,如果摸到2个红球算小亮赢,摸到1红1蓝,算小强赢,摸到2蓝不分输赢,重摸。他们俩谁获胜的可能性大?
小亮赢的情形只有一种,而小强赢的情形有四种,很明显,小强获胜的可能性大。
1
1
2
1
1
2
1
2
小亮赢:
小强赢:
2
1
2
2
不分输赢:
先给盒子中的球做上标记,比如可以标记为 和 ,再列出他们俩赢的情形。
1
2
1
2
可能性越大,个体在总数中所占数量越多;
可能性越小,个体在总数中所占数量越少。
事件发生的可能性的大小能反映出个体的数量的多少:
可能性大小的应用
作业课件中的相关练习。
课后补充练习。
01
02
第4课时 可能性大小的应用
小学数学·五年级(上)·人教版
1. 进一步体会不确定现象的特点及事件发生的可能性的大小。
2. 经历事件发生的可能性大小的探索过程,能根据试验的统计结果进行判断和推测,知道事件发生的可能性的大小与物体数量的多少有关,进一步体会随机现象的统计规律性,能根据数据推测事件发生的可能性的大小。
3. 进一步培养求实态度和科学精神。
【重点】
进一步体会随机现象的统计规律性,能根据数据推测事件发生的可能性的大小。
【难点】
理解随机现象和统计规律之间的关系。
回顾交流:
一叠扑克牌中有12张红桃、6张黑桃和3张梅花。摸出哪种花色牌的可能性最大?为什么?
可能性最大
最多
小组活动:在装有红、黄两种颜色小球的盒子里摸球,每个小组的盒子里装的球都一样。每次摸出一个球,记录下颜色,再放回去摇匀,重复20次。
小组合作:记录从盒中摸20次的结果。
合作要求
1. 小组成员分工合作。
2. 每次摸球前要将盒子里的球摇匀。
3. 每次摸出一个球,再放回去,重复20次。
4. 每摸出一个球后记录下它的颜色,可以用画“正”字的方法来记录。
小组汇报,说说你们组的试验结果。
颜色 记 录 次 数
正正正 15
正 5
下面是八个小组的统计情况。
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
仔细观察上面的表格,你有什么发现?
每次都是摸出 的次数比 多。
盒子里是 多还是 多?
小组
摸出 的次数
摸出 的次数
下面是八个小组的统计情况。
被摸出次数多
被摸出的可能性大
数量多
被摸出次数少
被摸出的可能性小
数量少
的数量多, 的数量少。
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
小组
摸出 的次数
摸出 的次数
真的是这样吗?让我们来验证一下吧。
下面是八个小组的统计情况。
哇,盒子里果然是 多。
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
小组
摸出 的次数
摸出 的次数
由以上试验可知,事件发生的可能性的大小能反映出个体的数量的多少:
可能性越大,个体在总数中所占数量越多; 可能性越小,个体在总数中所占数量越少。
思考:
(1)如果再摸一次,摸出哪种颜色的球的可能性大?
(2)如果继续摸下去,结果是不是一定摸出红色球?
(3)如果要使摸出的黄球的可能性大,可以怎么办?
从盒子里摸出一个棋子,可能是蓝色、黄色或红色。
1. 从下面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
因为盒子里红色棋子最多,黄色棋子最少,所以摸出红色棋子的可能性最大,摸出黄色棋子的可能性最小。
1. 从下面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
2.
全班每人掷一次。
掷出 朝上的有___人,
掷出 朝上的有___人。
哪面朝上?
朝上的可能性大还是 朝上的可能性大?
两面朝上的可能性应该是相等的。可为什么出现一个多一个少的现象呢?
如果有更多的人来掷,结果会怎样呢?
5红面1蓝面, 4红面2蓝面。
3. 给 涂上红、蓝两种颜色,要使掷出红色面朝上的可能性比蓝色面大,应该怎么涂?
红色面应比蓝色面多。
或5红1蓝。
所以可以涂 4红2蓝
共6个面
1.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上的数字应该怎样填?请你填一填。
1
1
1
1
1
1
1
1
5
卡片中 “1”的张数要最多;
卡片中 “5”的张数要最少。
1
1
1
1
1
1
1
1
1
5
5
1
1
1
1
1
1
1
2
2
5
1
1
1
1
1
1
4
4
4
5
10张卡片中可以只有“1”和“5”两个数字,也可以有其他数字。
1.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上可以是什么数字?请你填一填。
(1)
(2)
2. 小宇要设计一个转盘,上面画着 和 两种图案。如果要达到下面的要求,他该怎么画?
(1)任意转动1次,转到 的可能性大。
(2)任意转动1次,一定转到 。
的数量要多
都是
(答案不唯一)
(3)
(4)
(3)任意转动1次,转到 和 的可能性一样大。
(4)任意转到1次,不可能转到 。
和 的数量一样多
只有 ,没有
3. 小亮和小强玩摸球游戏(盒子里的球如右图所示)。一次摸 2个球,摸后放回,如果摸到2个红球算小亮赢,摸到1红1蓝,算小强赢,摸到2蓝不分输赢,重摸。他们俩谁获胜的可能性大?
小亮赢的情形只有一种,而小强赢的情形有四种,很明显,小强获胜的可能性大。
1
1
2
1
1
2
1
2
小亮赢:
小强赢:
2
1
2
2
不分输赢:
先给盒子中的球做上标记,比如可以标记为 和 ,再列出他们俩赢的情形。
1
2
1
2
可能性越大,个体在总数中所占数量越多;
可能性越小,个体在总数中所占数量越少。
事件发生的可能性的大小能反映出个体的数量的多少:
可能性大小的应用
作业课件中的相关练习。
课后补充练习。
01
02
