简易方程——实际问题与方程(1)(课件)(共31张PPT)-五年级上册数学人教版
文档属性
| 名称 | 简易方程——实际问题与方程(1)(课件)(共31张PPT)-五年级上册数学人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-23 12:16:53 | ||
图片预览










文档简介
(共31张PPT)
简易方程
5
实际问题与方程(1)
人教版五年级上册
从图中你获取了哪些数学信息?
小明在校运动会跳远比赛中以4.21 m的成绩打破学校纪录,超过原纪录0.06 m。学校原跳远纪录是多少米?
知识点:用形如x±a=b的方程解决简单的实际问题。
已知条件 成绩为4.21m,超过原纪录0.06m。
所求问题 学校原跳远纪录是多少米?
说一说你的解答方法。
4.21-0.06=4.15(米)
算术方法
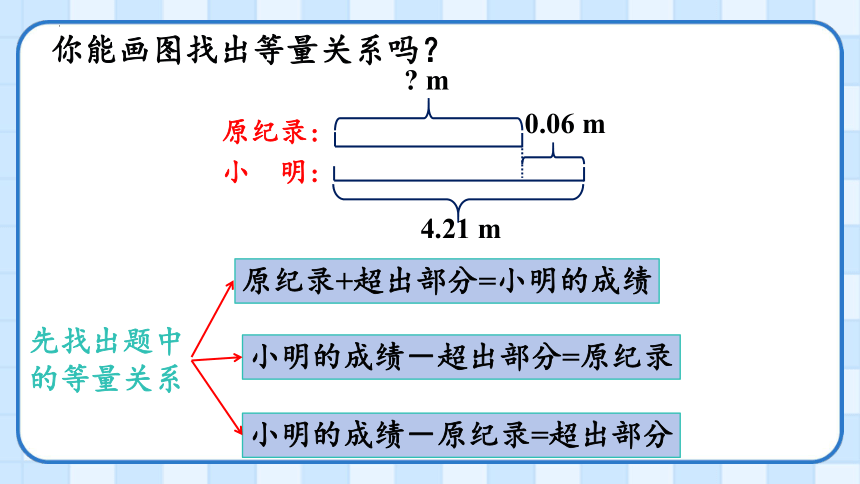
你能画图找出等量关系吗?
原纪录:
小 明:
m
0.06 m
4.21 m
原纪录+超出部分=小明的成绩
先找出题中
的等量关系
小明的成绩-超出部分=原纪录
小明的成绩-原纪录=超出部分
由于原纪录是未知数,可以把它设为x m,列方程解答。
解:设学校原跳远纪录是x m。
x+0.06=4.21
x+0.06-0.06=4.21-0.06
x=4.15
答:学校原跳远纪录是4.15m。
方程一:
原纪录+超出部分=小明的成绩
别忘了检验!
检验:
方程左边=x+0.06
=4.15+0.06
=4.21
=方程右边
所以,x=4.15是原方程的解。
还可以怎么列方程?
解:设学校原跳远纪录是x米。
4.21-x=0.06
4.21-x+x =0.06+x
4.21=0.06+x
0.06+x=4.21
0.06+x-0.06=4.21-0.06
x=4.15
小明的成绩-原纪录=超出部分
方程二:
答:学校原跳远纪录是4.15m。
别忘了检验!
检验:
方程左边=4.21-x
=4.21-4.15
=0.06
=方程右边
所以,x=4.15是原方程的解。
同一个问题,我们用了哪几种不同的方法解决?
算术的方法和列方程解答的方法。
用方程的思路解决问题时,你认为关键是什么?
找出等量关系。
一般来说,同一等量关系,
用加法表示比用减法表示更容易思考;
用乘法表示比用除法表示更容易思考。
因此列方程时能用加法和乘法的,尽量不用减法和除法。
1. 列方程解决下面的问题。
解:设小明去年身高x米。
0.08+x = 1.53
0.08+x-0.08 = 1.53-0.08
x = 1.45
8 cm = 0.08 m
答:小明去年身高1.45米。
去年身高+长高部分=今年身高
(1)小明今年身高1.53 m,比去年长高了8 cm。小明
去年身高多少?
关键句
30x=1.8
30x÷30=1.8÷30
x=0.06
答:这个水龙头每分钟滴出0.06 kɡ水。
解:设一个滴水的水龙头每分钟浪费x kɡ水。
半小时=30分
(2)一个滴水的水龙头半小时共滴了1.8 kg水,这个水
龙头每分钟滴出多少水
每分钟滴水克数×时间=总克数
关键句
1. 列方程解决下面的问题。
2.说说各题中的等量关系,并列出方程。
(1)母鸡有30只,比公鸡多5只,公鸡有几只?
(2)甲数是18,是乙数的2倍,乙数是多少?
公鸡的数量+5 = 母鸡的数量
x+5 = 30
乙数×2 = 甲数
2x = 18
四 培优训练
先写出等量关系,再列方程求解。
1. 一根绳子长100m。剪去m,还剩34m。
剪去的长度
剩下的长度
=
全长
+
x+34=100
x+34 34=100 34
x=56
=
2. 一头大象重xt,一头蓝鲸的质量是一头大象的
24倍,一头蓝鲸重120t。
一头大象的质量
倍数
×
24x=120
24x÷24=120÷24
x=5
一头蓝鲸的质量
列方程解决实际问题的步骤
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,
列方程;
(3)解方程并检验作答。
请同学们观察情境图并说说从中知道了哪些信息。
易错点:不要遗漏了隐含条件。
足球上黑色的皮都是五边形的,白色的皮都是六边形的。白色皮共有20块,比黑色皮的2倍少4块。黑色皮共有多少块?
已知条件 白色皮共20块,比黑色皮的2倍少4块
所求问题 共有多少块黑色皮?
怎样列方程呢?
先找出问题中的等量关系。
4块
20块
黑色皮
白色皮
2x块
x块
黑色皮块数×2-白色皮块数=4
黑色皮块数×2=白色皮块数+4
2x-4=20
2x-4+4=20+4
2x=24
你是怎样列方程的?记住最后要检验。
解:设黑色皮共有x 块。
x=12
2x÷2=24÷2
把什么看作一个整体
黑色皮有12块。
把2x看作一个整体
把x=12代入原方程中,
左边=2×12 - 4=24-4=20
右边=20
左边=右边
所以x=12是原方程的解。
怎样检验结果对不对呢?
2x - 4 = 20
还可以怎样列方程呢?
解:设黑色皮共有x块。
2x=20+4
x=12
2x÷2=24÷2
2x=24
答:黑色皮共有12块。
黑色皮块数 ×2 = 白色皮块数+4
大家回想一下,列方程解决实际问题有哪些步骤?
①弄清题意,设未知数为x。 设
②分析实际问题中的数量关系,找出等量关系。 找(关键)
③列出方程。 列
④解方程。 解
⑤检验并作答。 验
1. 1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
解:设一共装了x筒。
5x+3 = 1428
5x+3-3 = 1428-3
5x = 1425
5x÷5 = 1425÷5
x = 285
答:一共装了285筒。
装筒的个数+剩下的个数=总个数
课 堂 检 测
2.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。天安门广场的面积是多少万平方米?
解:设天安门广场的面积是x万平方米。
2x-16=72
2x-16+16=72+16
2x=88
2x÷2=88÷2
x=44
答:天安门广场的面积是44万平方米。
解:设同心县年平均降水量是x毫米。
8x+109=2325
8x+109-109=2325-109
8x=2216
8x÷8=2216÷8
x=277
答:同心县年平均降水量是277毫米。
3.宁夏的同心县是一个“干渴”的地区,年平均蒸发量是2325 mm,比年平均降水量的8倍还多109mm。同心县的年平均降水量是多少毫米?
4.把下列各题的等量关系补充完整,并列出方程。
1. 一张桌子售价110元,比一把椅子售价的4倍便
宜16元,一把椅子x元。
一把椅子售价的4倍
16元
=
一张桌子的售价
方程:
4x 16=110
5. 小明买了14支彩笔,每支彩笔x元,付给售货员30
元,找回了2元。
买14支水彩笔的钱数
找回的钱
=
付给售货员的钱
方程:
14x+2=30
6.小丽的年龄是多少岁?
x+4x 5=50
5x 5=50
解:设小丽的年龄是x岁。
5x 5+5=50+5
5x=55
小丽
爸爸
我的年龄比你的4倍小5岁。
我们的年龄加起来恰好是50岁。
5x÷5=55÷5
答:小丽的年龄是11岁。
x=11
7.蓝鲸的寿命大约是100年,比海象的3倍少20年。
海象的寿命大约是多少年?
解:设海象寿命大约是 x 年。
答:海象的寿命大约是40年。
3x-20=100
3x-20+20=100+20
3x=120
3x÷3=120÷3
x=40
海象寿命×3-20=蓝鲸寿命
这节课你们都学会了哪些知识?
x±a = b的应用
列方程解决实际问题的步骤:
关键
找出未知数x;
分析数量关系,找出等量关系,列方程;
解方程并检验作答。
ax±b=c的应用
先把ax看作一个整体
解形如ax±b=c的方程
求出ax等于多少
再求x等于多少
简易方程
5
实际问题与方程(1)
人教版五年级上册
从图中你获取了哪些数学信息?
小明在校运动会跳远比赛中以4.21 m的成绩打破学校纪录,超过原纪录0.06 m。学校原跳远纪录是多少米?
知识点:用形如x±a=b的方程解决简单的实际问题。
已知条件 成绩为4.21m,超过原纪录0.06m。
所求问题 学校原跳远纪录是多少米?
说一说你的解答方法。
4.21-0.06=4.15(米)
算术方法
你能画图找出等量关系吗?
原纪录:
小 明:
m
0.06 m
4.21 m
原纪录+超出部分=小明的成绩
先找出题中
的等量关系
小明的成绩-超出部分=原纪录
小明的成绩-原纪录=超出部分
由于原纪录是未知数,可以把它设为x m,列方程解答。
解:设学校原跳远纪录是x m。
x+0.06=4.21
x+0.06-0.06=4.21-0.06
x=4.15
答:学校原跳远纪录是4.15m。
方程一:
原纪录+超出部分=小明的成绩
别忘了检验!
检验:
方程左边=x+0.06
=4.15+0.06
=4.21
=方程右边
所以,x=4.15是原方程的解。
还可以怎么列方程?
解:设学校原跳远纪录是x米。
4.21-x=0.06
4.21-x+x =0.06+x
4.21=0.06+x
0.06+x=4.21
0.06+x-0.06=4.21-0.06
x=4.15
小明的成绩-原纪录=超出部分
方程二:
答:学校原跳远纪录是4.15m。
别忘了检验!
检验:
方程左边=4.21-x
=4.21-4.15
=0.06
=方程右边
所以,x=4.15是原方程的解。
同一个问题,我们用了哪几种不同的方法解决?
算术的方法和列方程解答的方法。
用方程的思路解决问题时,你认为关键是什么?
找出等量关系。
一般来说,同一等量关系,
用加法表示比用减法表示更容易思考;
用乘法表示比用除法表示更容易思考。
因此列方程时能用加法和乘法的,尽量不用减法和除法。
1. 列方程解决下面的问题。
解:设小明去年身高x米。
0.08+x = 1.53
0.08+x-0.08 = 1.53-0.08
x = 1.45
8 cm = 0.08 m
答:小明去年身高1.45米。
去年身高+长高部分=今年身高
(1)小明今年身高1.53 m,比去年长高了8 cm。小明
去年身高多少?
关键句
30x=1.8
30x÷30=1.8÷30
x=0.06
答:这个水龙头每分钟滴出0.06 kɡ水。
解:设一个滴水的水龙头每分钟浪费x kɡ水。
半小时=30分
(2)一个滴水的水龙头半小时共滴了1.8 kg水,这个水
龙头每分钟滴出多少水
每分钟滴水克数×时间=总克数
关键句
1. 列方程解决下面的问题。
2.说说各题中的等量关系,并列出方程。
(1)母鸡有30只,比公鸡多5只,公鸡有几只?
(2)甲数是18,是乙数的2倍,乙数是多少?
公鸡的数量+5 = 母鸡的数量
x+5 = 30
乙数×2 = 甲数
2x = 18
四 培优训练
先写出等量关系,再列方程求解。
1. 一根绳子长100m。剪去m,还剩34m。
剪去的长度
剩下的长度
=
全长
+
x+34=100
x+34 34=100 34
x=56
=
2. 一头大象重xt,一头蓝鲸的质量是一头大象的
24倍,一头蓝鲸重120t。
一头大象的质量
倍数
×
24x=120
24x÷24=120÷24
x=5
一头蓝鲸的质量
列方程解决实际问题的步骤
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,
列方程;
(3)解方程并检验作答。
请同学们观察情境图并说说从中知道了哪些信息。
易错点:不要遗漏了隐含条件。
足球上黑色的皮都是五边形的,白色的皮都是六边形的。白色皮共有20块,比黑色皮的2倍少4块。黑色皮共有多少块?
已知条件 白色皮共20块,比黑色皮的2倍少4块
所求问题 共有多少块黑色皮?
怎样列方程呢?
先找出问题中的等量关系。
4块
20块
黑色皮
白色皮
2x块
x块
黑色皮块数×2-白色皮块数=4
黑色皮块数×2=白色皮块数+4
2x-4=20
2x-4+4=20+4
2x=24
你是怎样列方程的?记住最后要检验。
解:设黑色皮共有x 块。
x=12
2x÷2=24÷2
把什么看作一个整体
黑色皮有12块。
把2x看作一个整体
把x=12代入原方程中,
左边=2×12 - 4=24-4=20
右边=20
左边=右边
所以x=12是原方程的解。
怎样检验结果对不对呢?
2x - 4 = 20
还可以怎样列方程呢?
解:设黑色皮共有x块。
2x=20+4
x=12
2x÷2=24÷2
2x=24
答:黑色皮共有12块。
黑色皮块数 ×2 = 白色皮块数+4
大家回想一下,列方程解决实际问题有哪些步骤?
①弄清题意,设未知数为x。 设
②分析实际问题中的数量关系,找出等量关系。 找(关键)
③列出方程。 列
④解方程。 解
⑤检验并作答。 验
1. 1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
解:设一共装了x筒。
5x+3 = 1428
5x+3-3 = 1428-3
5x = 1425
5x÷5 = 1425÷5
x = 285
答:一共装了285筒。
装筒的个数+剩下的个数=总个数
课 堂 检 测
2.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。天安门广场的面积是多少万平方米?
解:设天安门广场的面积是x万平方米。
2x-16=72
2x-16+16=72+16
2x=88
2x÷2=88÷2
x=44
答:天安门广场的面积是44万平方米。
解:设同心县年平均降水量是x毫米。
8x+109=2325
8x+109-109=2325-109
8x=2216
8x÷8=2216÷8
x=277
答:同心县年平均降水量是277毫米。
3.宁夏的同心县是一个“干渴”的地区,年平均蒸发量是2325 mm,比年平均降水量的8倍还多109mm。同心县的年平均降水量是多少毫米?
4.把下列各题的等量关系补充完整,并列出方程。
1. 一张桌子售价110元,比一把椅子售价的4倍便
宜16元,一把椅子x元。
一把椅子售价的4倍
16元
=
一张桌子的售价
方程:
4x 16=110
5. 小明买了14支彩笔,每支彩笔x元,付给售货员30
元,找回了2元。
买14支水彩笔的钱数
找回的钱
=
付给售货员的钱
方程:
14x+2=30
6.小丽的年龄是多少岁?
x+4x 5=50
5x 5=50
解:设小丽的年龄是x岁。
5x 5+5=50+5
5x=55
小丽
爸爸
我的年龄比你的4倍小5岁。
我们的年龄加起来恰好是50岁。
5x÷5=55÷5
答:小丽的年龄是11岁。
x=11
7.蓝鲸的寿命大约是100年,比海象的3倍少20年。
海象的寿命大约是多少年?
解:设海象寿命大约是 x 年。
答:海象的寿命大约是40年。
3x-20=100
3x-20+20=100+20
3x=120
3x÷3=120÷3
x=40
海象寿命×3-20=蓝鲸寿命
这节课你们都学会了哪些知识?
x±a = b的应用
列方程解决实际问题的步骤:
关键
找出未知数x;
分析数量关系,找出等量关系,列方程;
解方程并检验作答。
ax±b=c的应用
先把ax看作一个整体
解形如ax±b=c的方程
求出ax等于多少
再求x等于多少
