2.2.3直线的一般式方程 课件(共24张PPT)
文档属性
| 名称 | 2.2.3直线的一般式方程 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-25 15:17:04 | ||
图片预览






文档简介
(共24张PPT)
2.2.3直线的一般式方程
CONTENTS
ONE
学习目标
问题导入
探究新知
典例解析
TWO
THRRE
FOUR
学习目标
了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系;
能正确地进行直线的一般式方程与特殊形式的方程的转化;
能运用直线的一般式方程解决有关问题.
重点:了解二元一次方程与直线的对应关系,掌握直线的一般形式;
难点:能根据所给条件求直线方程,并能在几种形式间相互转化.
问题导入
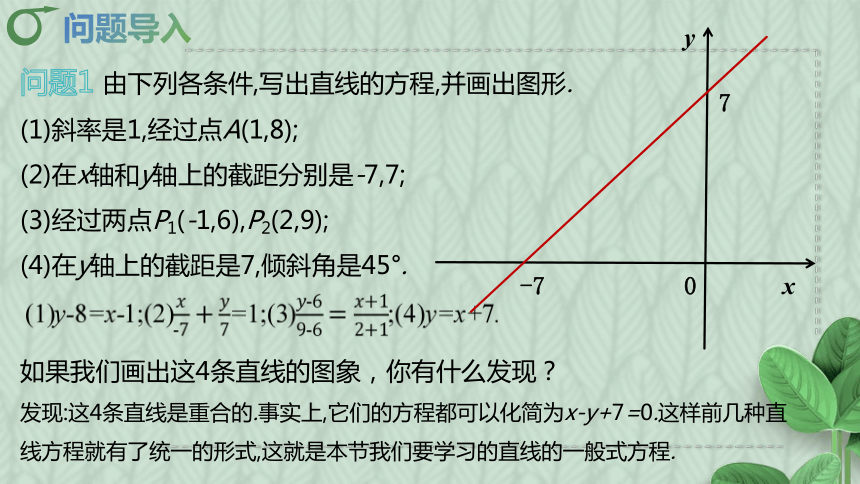
问题1 由下列各条件,写出直线的方程,并画出图形.
(1)斜率是1,经过点A(1,8);
(2)在x轴和y轴上的截距分别是-7,7;
(3)经过两点P1(-1,6),P2(2,9);
(4)在y轴上的截距是7,倾斜角是45°.
如果我们画出这4条直线的图象,你有什么发现?
x
0
y
-7
7
发现:这4条直线是重合的.事实上,它们的方程都可以化简为x-y+7=0.这样前几种直线方程就有了统一的形式,这就是本节我们要学习的直线的一般式方程.
探究新知
直线的一般式方程
(1)在平面直角坐标系中,对于任何一条直线,都有一个表示这条直线的关于x,y的_ ____________;任何关于x,y的二元一次方程都表示________.方程_____________________________________ 叫做直线方程的一般式.
(2)直线一般式方程的结构特征
①方程是关于x,y的二元一次方程.
②方程中等号的左侧自左向右一般按x,y常数的先后顺序排列.
③x的系数一般不为分数和负数.
④虽然直线方程的一般式有三个参数,但只需两个独立的条件即可求得直线的方程.
二元一次方程
一条直线
Ax+By+C=0(其中A、B不同时为0)
探究新知
直线方程的五种表达方式:
5种形式 方程 局限性 各常数的几何意义
点斜式 不能表示与x轴垂直的直线 ()是直线上一定点,
k是斜率
斜截式 不能表示与x轴垂直的直线 k是斜率,b是y轴上的截距
两点式 不能表示与x轴、y轴垂直的直线 ()、()是直线上两个不同定点
截距式 不能表示与x轴垂直、y轴垂直、过原点的直线 a是x轴上的非零截距,
b是y轴上的非零截距
一般式 表示所有的直线 当B≠0时,-是斜率,
-是y轴上的截距
探究新知
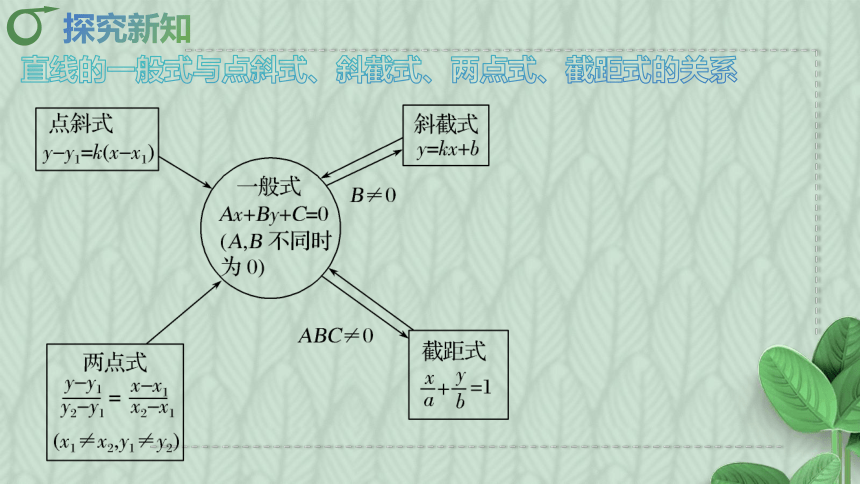
直线的一般式与点斜式、斜截式、两点式、截距式的关系
探究新知
线段的中点坐标公式
若点P1,P2的坐标分别为(x1,y1),(x2,y2),设P(x,y)是线段P1P2的中点,
则
探究新知
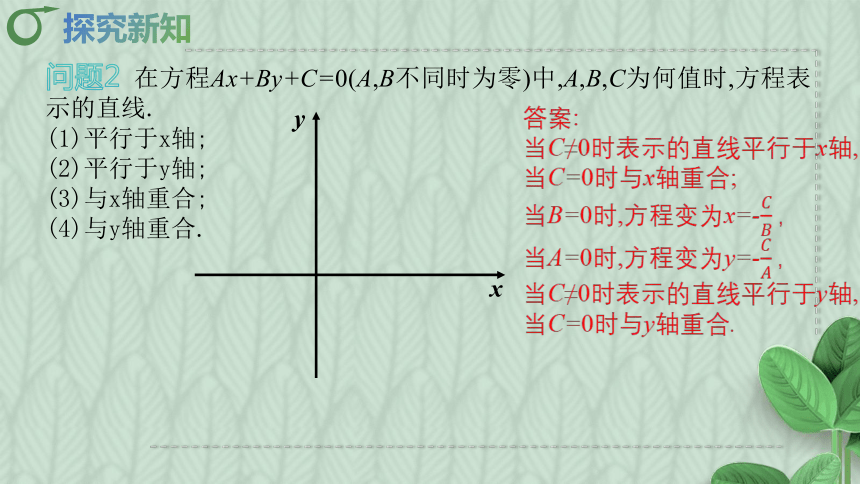
问题2 在方程Ax+By+C=0(A,B不同时为零)中,A,B,C为何值时,方程表示的直线.
(1)平行于x轴;
(2)平行于y轴;
(3)与x轴重合;
(4)与y轴重合.
答案:
当C≠0时表示的直线平行于x轴,
当C=0时与x轴重合;
当B=0时,方程变为x=-
当A=0时,方程变为y=-
当C≠0时表示的直线平行于y轴,
当C=0时与y轴重合.
y
x
问题3
直线方程2x+3y+1=0化为斜截式为 ;
化为截距式为 .
探究新知
两条直线的位置关系
斜截式 一般式
方程 y=, y= x+y+=0(+)
x+y+=0(+)
相交 -0
垂直 =-1 +
平行 = = 0 或 = 0
-0 -0
重合 = = 0,
且0
探究新知
探究新知
问题3 判断下列两组直线是否平行或垂直
(1) ; 行
(2); 平行
(3); 垂直
(4) 垂直
典例解析
例1 根据下列条件分别写出直线的方程,并化为一般式方程.
(1)斜率是-,经过点A(8,―2);
(2)经过点B(4,2),平行于x轴;
(3)在x轴和y轴上的截距分别是,―3;
(4)经过两点(3,―2),(5,―4).
由点斜式方程得 ,化成一般式得x+2y―4=0.
由斜截式得y=2,化为一般式得y―2=0.
由截距式得 ,化成一般式得2x―y―3=0.
由两点式得 ,化成一般式方程为
.
典例解析
变式1 已知直线l经过点B(3,-1),且倾斜角是30°,求直线的点斜式方程和一般式方程.
【解析】
因为直线倾斜角是30°,所以直线的斜率
所以直线的点斜式方程为
化成一般式方程为
典例解析
例2 △ABC的一个顶点为A(-1,-4),∠B、∠C 的平分线在直线y+1=0和x+y+1=0上,求直线BC的方程.
典例解析
例3 求与直线3x+4y+1=0平行且过点(1,2)的直线l的方程.
解:
设与直线3x+4y+1=0平行的直线l的方程为:3x+4y+m=0,
∵l经过点(1,2),
∴3×1+4×2+m=0,解得m=―11.
∴所求直线方程为3x+4y―11=0.
典例解析
变式1
已知直线:3mx+8y+3m-10=0 和 :x+6my-4=0 .问 m为何值时:
(1)与平行
(2)与垂直.
【解析】
当m=0时,:8y-10=0;:x-4=0,
当m0时,: ;:
由 ,得 ,由 得
而 无解
综上所述(1) ,与平行.
(2) ,与垂直.
典例解析
变式2 求经过点A(2,1),且与直线2x+y―10=0垂直的直线l的方程.
【解析】因为直线l与直线2x+y―10=0垂直,可设直线l的方程为,
把点A(2,1)代入直线l的方程得:m=0,
所以直线l的方程为:x-2y=0.
典例解析
1.利用一般式解决直线平行与垂直问题的策略
直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,
(1)若l1∥l2 A1B2-A2B1=0且B1C2-B2C1≠0(或A1C2-A2C1≠0).
(2)若l1⊥l2 A1A2+B1B2=0.
2.与已知直线平行(垂直)的直线方程的求法
(1)与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0(m≠C).
(2)与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+m=0.
典例解析
练习 已知直线l的方程为3x+4y-12=0,求直线l'的方程,l'满足
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
基础达标
1.直线x-y+2=0的倾斜角是( )
A.30° B.45° C.60° D.90°
解析由x-y+2=0,得y=x+2.其斜率为1,倾斜角为45°.
2.直线l的方程为Ax+By+C=0,若直线l过原点和二、四象限,则( )
A.C=0,B>0 B.A>0,B>0,C=0 C.AB<0,C=0 D.AB>0,C=0
4.已知点M(1,2)在直线l上的射影是H(-1,4),则直线l的方程为( )
A.x-y+5=0 B.x-y-3=0 C.x+y-5=0 D.x-y+1=0
解析∵kMH==-1,∴直线l的斜率k=1,∴直线l的方程为y-4=x+1,即x-y+5=0.
7.过点P(2,-1)且与直线y+2x-5=0平行的直线方程是 .
解析设要求的直线方程为2x+y+m=0,把P(2,-1)代入直线方程可得4-1+m=0,解得m=-3,∴要求的直线方程为2x+y-3=0.
8.若直线l的方程为y-a=(a-1)(x+2),且l在y轴上的截距为6,则a= .
B
D
A
2x+y-3=0
典例解析
9.(多选题)直线l1:ax-y+b=0与直线l2:bx+y-a=0(ab≠0)的图象可能是( )
BC
10.已知直线l1:(m+2)x+(m+3)y-5=0和l2:6x+(2m-1)y=5.当m为何值时,有:
(1)l1∥l2
(2)l1⊥l2
解:(1)由(m+2)(2m-1)=6(m+3),
得m=4或m=-当m=4时,l1:6x+7y-5=0,l2:6x+7y=5,即l1与l2重合;当m=-时,l1:-x+y-5=0,l2:6x-6y-5=0,即l1∥l2.故当m=-时,l1∥l2.
(2)由6(m+2)+(m+3)(2m-1)=0,得m=-1或m=-.
故当m=-1或m=时,l1⊥l2.
小结
THANK
YOU
2.2.3直线的一般式方程
CONTENTS
ONE
学习目标
问题导入
探究新知
典例解析
TWO
THRRE
FOUR
学习目标
了解直线的一般式方程的形式特征,理解直线的一般式方程与二元一次方程的关系;
能正确地进行直线的一般式方程与特殊形式的方程的转化;
能运用直线的一般式方程解决有关问题.
重点:了解二元一次方程与直线的对应关系,掌握直线的一般形式;
难点:能根据所给条件求直线方程,并能在几种形式间相互转化.
问题导入
问题1 由下列各条件,写出直线的方程,并画出图形.
(1)斜率是1,经过点A(1,8);
(2)在x轴和y轴上的截距分别是-7,7;
(3)经过两点P1(-1,6),P2(2,9);
(4)在y轴上的截距是7,倾斜角是45°.
如果我们画出这4条直线的图象,你有什么发现?
x
0
y
-7
7
发现:这4条直线是重合的.事实上,它们的方程都可以化简为x-y+7=0.这样前几种直线方程就有了统一的形式,这就是本节我们要学习的直线的一般式方程.
探究新知
直线的一般式方程
(1)在平面直角坐标系中,对于任何一条直线,都有一个表示这条直线的关于x,y的_ ____________;任何关于x,y的二元一次方程都表示________.方程_____________________________________ 叫做直线方程的一般式.
(2)直线一般式方程的结构特征
①方程是关于x,y的二元一次方程.
②方程中等号的左侧自左向右一般按x,y常数的先后顺序排列.
③x的系数一般不为分数和负数.
④虽然直线方程的一般式有三个参数,但只需两个独立的条件即可求得直线的方程.
二元一次方程
一条直线
Ax+By+C=0(其中A、B不同时为0)
探究新知
直线方程的五种表达方式:
5种形式 方程 局限性 各常数的几何意义
点斜式 不能表示与x轴垂直的直线 ()是直线上一定点,
k是斜率
斜截式 不能表示与x轴垂直的直线 k是斜率,b是y轴上的截距
两点式 不能表示与x轴、y轴垂直的直线 ()、()是直线上两个不同定点
截距式 不能表示与x轴垂直、y轴垂直、过原点的直线 a是x轴上的非零截距,
b是y轴上的非零截距
一般式 表示所有的直线 当B≠0时,-是斜率,
-是y轴上的截距
探究新知
直线的一般式与点斜式、斜截式、两点式、截距式的关系
探究新知
线段的中点坐标公式
若点P1,P2的坐标分别为(x1,y1),(x2,y2),设P(x,y)是线段P1P2的中点,
则
探究新知
问题2 在方程Ax+By+C=0(A,B不同时为零)中,A,B,C为何值时,方程表示的直线.
(1)平行于x轴;
(2)平行于y轴;
(3)与x轴重合;
(4)与y轴重合.
答案:
当C≠0时表示的直线平行于x轴,
当C=0时与x轴重合;
当B=0时,方程变为x=-
当A=0时,方程变为y=-
当C≠0时表示的直线平行于y轴,
当C=0时与y轴重合.
y
x
问题3
直线方程2x+3y+1=0化为斜截式为 ;
化为截距式为 .
探究新知
两条直线的位置关系
斜截式 一般式
方程 y=, y= x+y+=0(+)
x+y+=0(+)
相交 -0
垂直 =-1 +
平行 = = 0 或 = 0
-0 -0
重合 = = 0,
且0
探究新知
探究新知
问题3 判断下列两组直线是否平行或垂直
(1) ; 行
(2); 平行
(3); 垂直
(4) 垂直
典例解析
例1 根据下列条件分别写出直线的方程,并化为一般式方程.
(1)斜率是-,经过点A(8,―2);
(2)经过点B(4,2),平行于x轴;
(3)在x轴和y轴上的截距分别是,―3;
(4)经过两点(3,―2),(5,―4).
由点斜式方程得 ,化成一般式得x+2y―4=0.
由斜截式得y=2,化为一般式得y―2=0.
由截距式得 ,化成一般式得2x―y―3=0.
由两点式得 ,化成一般式方程为
.
典例解析
变式1 已知直线l经过点B(3,-1),且倾斜角是30°,求直线的点斜式方程和一般式方程.
【解析】
因为直线倾斜角是30°,所以直线的斜率
所以直线的点斜式方程为
化成一般式方程为
典例解析
例2 △ABC的一个顶点为A(-1,-4),∠B、∠C 的平分线在直线y+1=0和x+y+1=0上,求直线BC的方程.
典例解析
例3 求与直线3x+4y+1=0平行且过点(1,2)的直线l的方程.
解:
设与直线3x+4y+1=0平行的直线l的方程为:3x+4y+m=0,
∵l经过点(1,2),
∴3×1+4×2+m=0,解得m=―11.
∴所求直线方程为3x+4y―11=0.
典例解析
变式1
已知直线:3mx+8y+3m-10=0 和 :x+6my-4=0 .问 m为何值时:
(1)与平行
(2)与垂直.
【解析】
当m=0时,:8y-10=0;:x-4=0,
当m0时,: ;:
由 ,得 ,由 得
而 无解
综上所述(1) ,与平行.
(2) ,与垂直.
典例解析
变式2 求经过点A(2,1),且与直线2x+y―10=0垂直的直线l的方程.
【解析】因为直线l与直线2x+y―10=0垂直,可设直线l的方程为,
把点A(2,1)代入直线l的方程得:m=0,
所以直线l的方程为:x-2y=0.
典例解析
1.利用一般式解决直线平行与垂直问题的策略
直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,
(1)若l1∥l2 A1B2-A2B1=0且B1C2-B2C1≠0(或A1C2-A2C1≠0).
(2)若l1⊥l2 A1A2+B1B2=0.
2.与已知直线平行(垂直)的直线方程的求法
(1)与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0(m≠C).
(2)与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+m=0.
典例解析
练习 已知直线l的方程为3x+4y-12=0,求直线l'的方程,l'满足
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
基础达标
1.直线x-y+2=0的倾斜角是( )
A.30° B.45° C.60° D.90°
解析由x-y+2=0,得y=x+2.其斜率为1,倾斜角为45°.
2.直线l的方程为Ax+By+C=0,若直线l过原点和二、四象限,则( )
A.C=0,B>0 B.A>0,B>0,C=0 C.AB<0,C=0 D.AB>0,C=0
4.已知点M(1,2)在直线l上的射影是H(-1,4),则直线l的方程为( )
A.x-y+5=0 B.x-y-3=0 C.x+y-5=0 D.x-y+1=0
解析∵kMH==-1,∴直线l的斜率k=1,∴直线l的方程为y-4=x+1,即x-y+5=0.
7.过点P(2,-1)且与直线y+2x-5=0平行的直线方程是 .
解析设要求的直线方程为2x+y+m=0,把P(2,-1)代入直线方程可得4-1+m=0,解得m=-3,∴要求的直线方程为2x+y-3=0.
8.若直线l的方程为y-a=(a-1)(x+2),且l在y轴上的截距为6,则a= .
B
D
A
2x+y-3=0
典例解析
9.(多选题)直线l1:ax-y+b=0与直线l2:bx+y-a=0(ab≠0)的图象可能是( )
BC
10.已知直线l1:(m+2)x+(m+3)y-5=0和l2:6x+(2m-1)y=5.当m为何值时,有:
(1)l1∥l2
(2)l1⊥l2
解:(1)由(m+2)(2m-1)=6(m+3),
得m=4或m=-当m=4时,l1:6x+7y-5=0,l2:6x+7y=5,即l1与l2重合;当m=-时,l1:-x+y-5=0,l2:6x-6y-5=0,即l1∥l2.故当m=-时,l1∥l2.
(2)由6(m+2)+(m+3)(2m-1)=0,得m=-1或m=-.
故当m=-1或m=时,l1⊥l2.
小结
THANK
YOU
