1.3相似三角形的性质(同步课件)(共24张PPT)
文档属性
| 名称 | 1.3相似三角形的性质(同步课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-24 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
(青岛版)9年级
上
1.3 相似三角形的性质
第1章
“—”
一、什么叫两个三角形相似?
三、三角形相似的性质是什么?
二、三角形相似的判定方法有哪些?
1、相似三角形的对应角相等。
2、相似三角形的对应边成比例。
复习回顾
1. 理解相似三角形周长的比等于相似比,面积的比等于相似比的平方,相似三角形对应高的比也等于相似比;多边形的周长的比等于相似比,面积的比等于相似比的平方.
2. 能应用相似三角形的有关性质解决相关问题.
学习目标
A
C
B
A1
C1
B1
问题: △ABC与△A1B1C1相似吗?
新知导入
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和△A′B′C′的对应高AD和A′D′.
∵ △ABC∽△A′B′C′
∴ ∠B=∠B′
又 AD⊥BC,A′D′⊥B′C′
∴ ∠ADB=∠A′D′B′=90°
∴ △ABD∽△A′B′D′
∴
新知探究
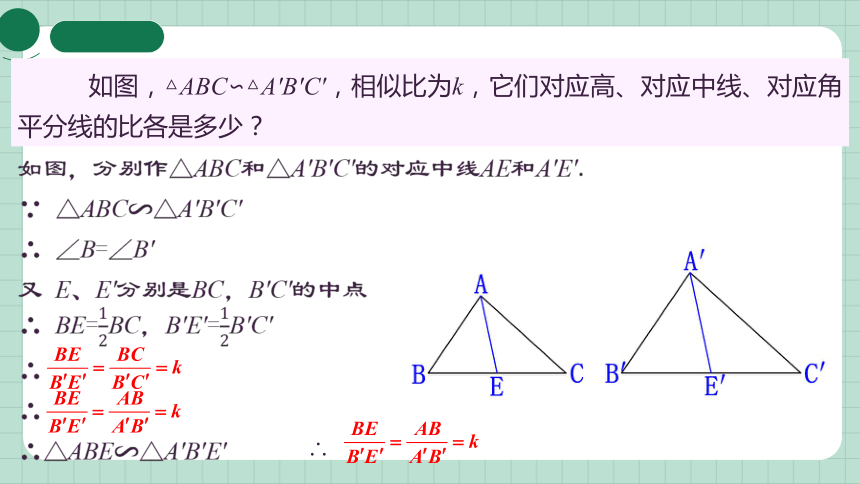
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和△A′B′C′的对应中线AE和A′E′.
∵ △ABC∽△A′B′C′
∴ ∠B=∠B′
又 E、E′分别是BC,B′C′的中点
∴ BE=BC,B′E′=B′C′
∴
∴
∴△ABE∽△A′B′E′
∴
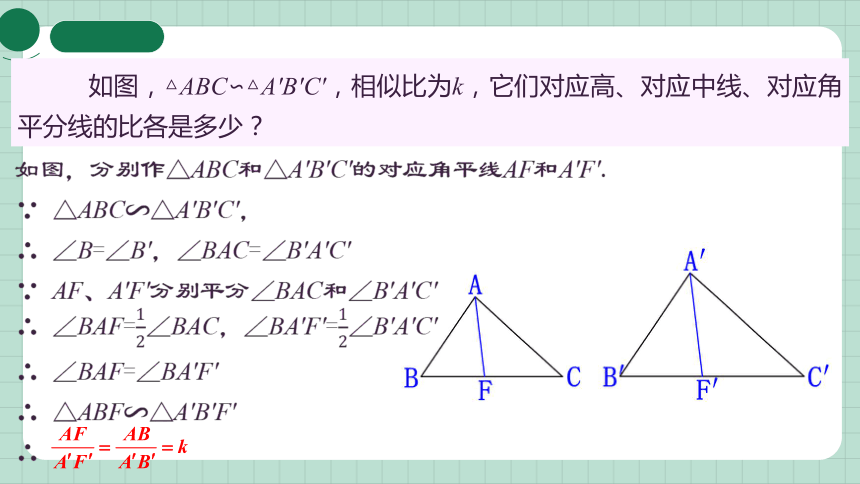
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和△A′B′C′的对应角平线AF和A′F′.
∵ △ABC∽△A′B′C′,
∴ ∠B=∠B′,∠BAC=∠B′A′C′
∵ AF、A′F′分别平分∠BAC和∠B′A′C′
∴ ∠BAF=∠BAC,∠BA′F′=∠B′A′C′
∴ ∠BAF=∠BA′F′
∴ △ABF∽△A′B′F′
∴
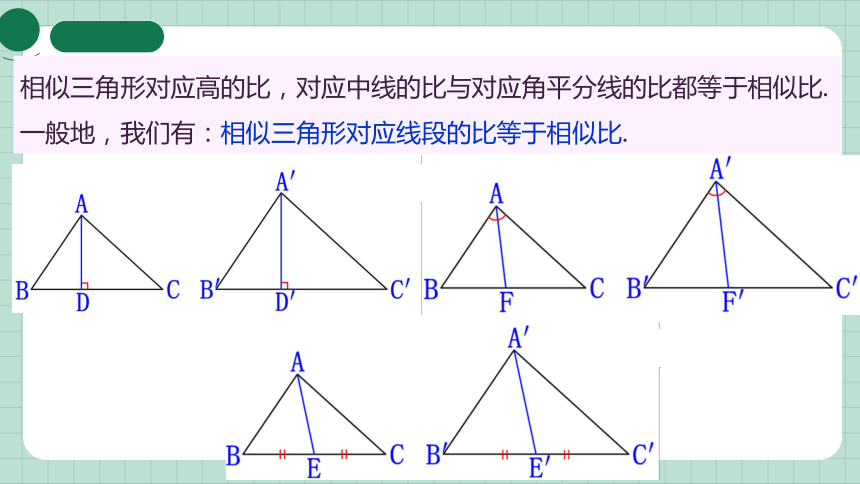
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
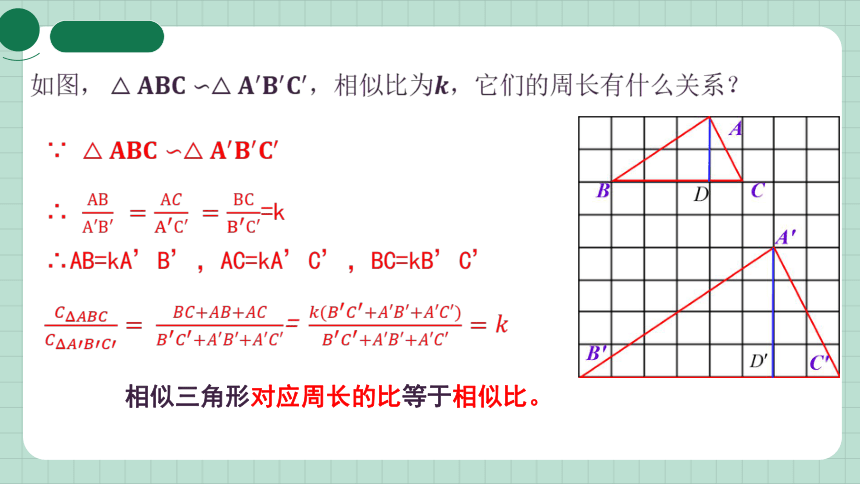
∵
∴ =k
∴AB=kA’B’,AC=kA’C’,BC=kB’C’
=
相似三角形对应周长的比等于相似比。
解:∵
∴ =k
则BC=kB’C’,AD=kA’D’
=
相似三角形对应面积的比等于相似比的平方。
3、相似三角形的对应角平分线、对应中
线和对应高线的比都等于相似比。
相似三角形的性质:
1、相似三角形的对应角相等。
2、相似三角形的对应边成比例。
4、相似三角形的周长的比等于相似比。
5、相似三角形的面积的比等于相似比
的平方。
例:如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60 cm,AD= 40 cm,四边形PQRS是正方形.
(1)AE是Δ ASR的高吗?为什么?
(2) ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
(1)AE是ΔASR的高吗?为什么?
解: AE是ΔASR的高.
理由:
∵AD是ΔABC的高,
∴ ∠ADC=90°.
∵四边形PQRS是正方形,
∴SR∥BC.
∴∠AER=∠ADC=90°.
∴ AE是ΔASR的高.
S
R
Q
P
E
D
C
B
A
(2) ΔASR与ΔABC相似吗?为什么?
解: ΔASR与ΔABC相似. 理由:
∵ SR∥BC,
∴ ∠ASR=∠B, ∠ARS=∠C.
∴ ΔASR与ΔABC相似.
S
R
Q
P
E
D
C
B
A
(3)求正方形PQRS的边长.
是方程思想哦!
解:∵ ΔASR ∽ ΔABC,
AE,AD分别是ΔASR 和ΔABC
对应边上的高,
∴ .
设正方形PQRS的边长为 x cm,
则SR=DE=x cm,AE=(40-x)cm.
∴ 解得x=24.
∴正方形PQRS的边长为24 cm.
S
R
Q
P
E
D
C
B
A
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2. △ABC 与 △A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =_______ .
课堂练习
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2. △ABC 与 △A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =_______ .
2 : 3
2 : 3
16 cm
3、一个三角形的各边长扩大为原来的5倍,这个三角形的周长扩大为原来的 倍;
4、一个四边形的各边长扩大为原来的9倍,这个四边形的面积扩大为原来的 倍.
5
81
5. 两个相似三角形的一对对应边分别是 35 cm、14 cm,
(1) 它们的周长差 60 cm,这两个三角形的周长分别是________________;
(2) 它们的面积之和是 58 cm2,这两个三角形的面
积分别是______________.
100 cm、40 cm
50 cm2、8 cm2
6、如图,平行于BC的直线DE把△ABC分成的两部分面积相等.求
【解析】
∵DE∥BC,∴△ADE∽△ABC.
∴.
∵S△ADE=S四边形BCDE,
∴,即.
6、如图,平行于BC的直线DE把△ABC分成的两部分面积相等.求
3、相似三角形的对应角平分线、对应中
线和对应高线的比都等于相似比。
相似三角形的性质:
1、相似三角形的对应角相等。
2、相似三角形的对应边成比例。
4、相似三角形的周长的比等于相似比。
5、相似三角形的面积的比等于相似比
的平方。
课堂总结
1、课本24练习1,2
2、习题1.3,T1-6
作业布置
2
https://www.21cnjy.com/help/help_extract.php
(青岛版)9年级
上
1.3 相似三角形的性质
第1章
“—”
一、什么叫两个三角形相似?
三、三角形相似的性质是什么?
二、三角形相似的判定方法有哪些?
1、相似三角形的对应角相等。
2、相似三角形的对应边成比例。
复习回顾
1. 理解相似三角形周长的比等于相似比,面积的比等于相似比的平方,相似三角形对应高的比也等于相似比;多边形的周长的比等于相似比,面积的比等于相似比的平方.
2. 能应用相似三角形的有关性质解决相关问题.
学习目标
A
C
B
A1
C1
B1
问题: △ABC与△A1B1C1相似吗?
新知导入
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和△A′B′C′的对应高AD和A′D′.
∵ △ABC∽△A′B′C′
∴ ∠B=∠B′
又 AD⊥BC,A′D′⊥B′C′
∴ ∠ADB=∠A′D′B′=90°
∴ △ABD∽△A′B′D′
∴
新知探究
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和△A′B′C′的对应中线AE和A′E′.
∵ △ABC∽△A′B′C′
∴ ∠B=∠B′
又 E、E′分别是BC,B′C′的中点
∴ BE=BC,B′E′=B′C′
∴
∴
∴△ABE∽△A′B′E′
∴
如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?
如图,分别作△ABC和△A′B′C′的对应角平线AF和A′F′.
∵ △ABC∽△A′B′C′,
∴ ∠B=∠B′,∠BAC=∠B′A′C′
∵ AF、A′F′分别平分∠BAC和∠B′A′C′
∴ ∠BAF=∠BAC,∠BA′F′=∠B′A′C′
∴ ∠BAF=∠BA′F′
∴ △ABF∽△A′B′F′
∴
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
∵
∴ =k
∴AB=kA’B’,AC=kA’C’,BC=kB’C’
=
相似三角形对应周长的比等于相似比。
解:∵
∴ =k
则BC=kB’C’,AD=kA’D’
=
相似三角形对应面积的比等于相似比的平方。
3、相似三角形的对应角平分线、对应中
线和对应高线的比都等于相似比。
相似三角形的性质:
1、相似三角形的对应角相等。
2、相似三角形的对应边成比例。
4、相似三角形的周长的比等于相似比。
5、相似三角形的面积的比等于相似比
的平方。
例:如图,AD是ΔABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60 cm,AD= 40 cm,四边形PQRS是正方形.
(1)AE是Δ ASR的高吗?为什么?
(2) ΔASR与ΔABC相似吗?为什么?
(3)求正方形PQRS的边长.
S
R
Q
P
E
D
C
B
A
(1)AE是ΔASR的高吗?为什么?
解: AE是ΔASR的高.
理由:
∵AD是ΔABC的高,
∴ ∠ADC=90°.
∵四边形PQRS是正方形,
∴SR∥BC.
∴∠AER=∠ADC=90°.
∴ AE是ΔASR的高.
S
R
Q
P
E
D
C
B
A
(2) ΔASR与ΔABC相似吗?为什么?
解: ΔASR与ΔABC相似. 理由:
∵ SR∥BC,
∴ ∠ASR=∠B, ∠ARS=∠C.
∴ ΔASR与ΔABC相似.
S
R
Q
P
E
D
C
B
A
(3)求正方形PQRS的边长.
是方程思想哦!
解:∵ ΔASR ∽ ΔABC,
AE,AD分别是ΔASR 和ΔABC
对应边上的高,
∴ .
设正方形PQRS的边长为 x cm,
则SR=DE=x cm,AE=(40-x)cm.
∴ 解得x=24.
∴正方形PQRS的边长为24 cm.
S
R
Q
P
E
D
C
B
A
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2. △ABC 与 △A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =_______ .
课堂练习
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2. △ABC 与 △A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =_______ .
2 : 3
2 : 3
16 cm
3、一个三角形的各边长扩大为原来的5倍,这个三角形的周长扩大为原来的 倍;
4、一个四边形的各边长扩大为原来的9倍,这个四边形的面积扩大为原来的 倍.
5
81
5. 两个相似三角形的一对对应边分别是 35 cm、14 cm,
(1) 它们的周长差 60 cm,这两个三角形的周长分别是________________;
(2) 它们的面积之和是 58 cm2,这两个三角形的面
积分别是______________.
100 cm、40 cm
50 cm2、8 cm2
6、如图,平行于BC的直线DE把△ABC分成的两部分面积相等.求
【解析】
∵DE∥BC,∴△ADE∽△ABC.
∴.
∵S△ADE=S四边形BCDE,
∴,即.
6、如图,平行于BC的直线DE把△ABC分成的两部分面积相等.求
3、相似三角形的对应角平分线、对应中
线和对应高线的比都等于相似比。
相似三角形的性质:
1、相似三角形的对应角相等。
2、相似三角形的对应边成比例。
4、相似三角形的周长的比等于相似比。
5、相似三角形的面积的比等于相似比
的平方。
课堂总结
1、课本24练习1,2
2、习题1.3,T1-6
作业布置
2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
