人教版四年级下册数学 轴对称 教案
图片预览


文档简介
感受图形的位置与运动:轴对称
【案例简介】
内容分析:
“轴对称”是图形与几何领域典型的内容,属于“图形的位置与运动”版块,内容安排在第二学段(3-4年级),它不是静态的图形认识,与平移、旋转、缩放一起构成了图形运动的四种基本方式,所以突出运动和变化是轴对称教学的核心与关键,应是教学的深层追求。在第一学段(1-2年级)中,学生已经会辨认常见的平面图形,能直观描述图形的特征,对轴对称现象已有一定的认识基础,同时此处学习也为第三学段(5-6年级)利用四种基本变换设计图案奠定基础,更为第四学段(7-9年级)学习中心对称图形埋下伏笔,承前启后,具有一定的连续性和整体性。
教学目标:
1.通过观察和操作,认识对称现象和轴对称变换,并学会找对称轴。
2.能根据轴对称图形的特征,鼓励学生用多种方法验证对称图案,重点借助“翻折运动”培养学生的观察能力、动手能力、想象能力。
3.能利用轴对称的特点,在方格纸上补全简单的轴对称图形,在思维拓展中促进学生空间观念的发展。
4.感受物体或图形的对称美,体会学习数学的乐趣。
教学过程:
创设生活情境,初步感知轴对称;经历活动的过程,多角度感知图形的对称变换;思维提升与拓展,感受轴对称的结构美。
【标准要求】
内容要求:
认识轴对称图形和对称轴,能在方格纸上补全简单的轴对称图形;在感受图形位置与运动的过程中,增强空间观念和几何直观。
学业要求:
能认识现实生活中的轴对称图形,知道轴对称图形对称轴的数量,能在方格纸上补全轴对称图形。
教学提示:
图形运动的教学,可以通过有趣的活动或者长作业的方式,帮助学生感知轴对称的特征,增强对轴对称的理解,以增强学生的空间观念,帮助学生积累有计划、有条理做事的实践经验。
【案例解读】
一.创设生活情境,初步感知轴对称
(一)感知对称现象
1.同学们,这是什么?(逐个呈现:脸谱、树叶、剪纸、蝴蝶、天安门,引导学生依次回答名称。)它们有什么共同的特点呢?
2.脸谱、天安门、树叶、蝴蝶左右一样,剪纸上下一样,它们都是对称的。
(二)揭示课题
像这样两边都一样的现象我们称为“对称”现象,对称现象在生活中随处可见,我们把它们画下来就得到了“轴对称图形”,今天我们就来研究对称现象中的“轴对称图形”。
【解读:《标准》在教学提示中提出,图形运动的教学可以从有趣的活动入手,本案例中从学生熟悉生活场景中的对称现象直接导入新课,引导学生通过观察,初步感受一半和另一半一样的现象,初步了解什么是对称,感知对称现象在生活中无处不在。同时,对称现象与轴对称图形具有本质的区别,所以在揭示课题处有意识从“现象”过渡到“平面图形”,避免两者混为一谈。】
二、经历活动的过程,多角度感知图形的对称变换
(一)大任务驱动
1.下面的平面图形相信你都认识,平面图形中有些也是对称的,你能找到吗? 如果是对称图形,各有几条对称轴呢?试着把他们画出来。
( )条对称轴 ( )条对称轴 ( )条对称轴 ( )条对称轴
2.你打算怎么研究?请拿出学习材料单。
(二)汇报交流:你觉得哪些是对称的?你是怎么想的?
1.初步想象感知
(1)想一想,怎样判断一个图形是轴对称图形呢?
(2)有同学们建议可以在头脑中想象对折的操作,一个图形是不是只要对折就能判断了呢?
(3)没有地方突出来,另一半隐藏了,也就是要完全重合,你能在头脑中想象出来,这4个平面图形都是轴对称图形吗?
(4)学生静静地观察与思考一会。
2.学具操作感知
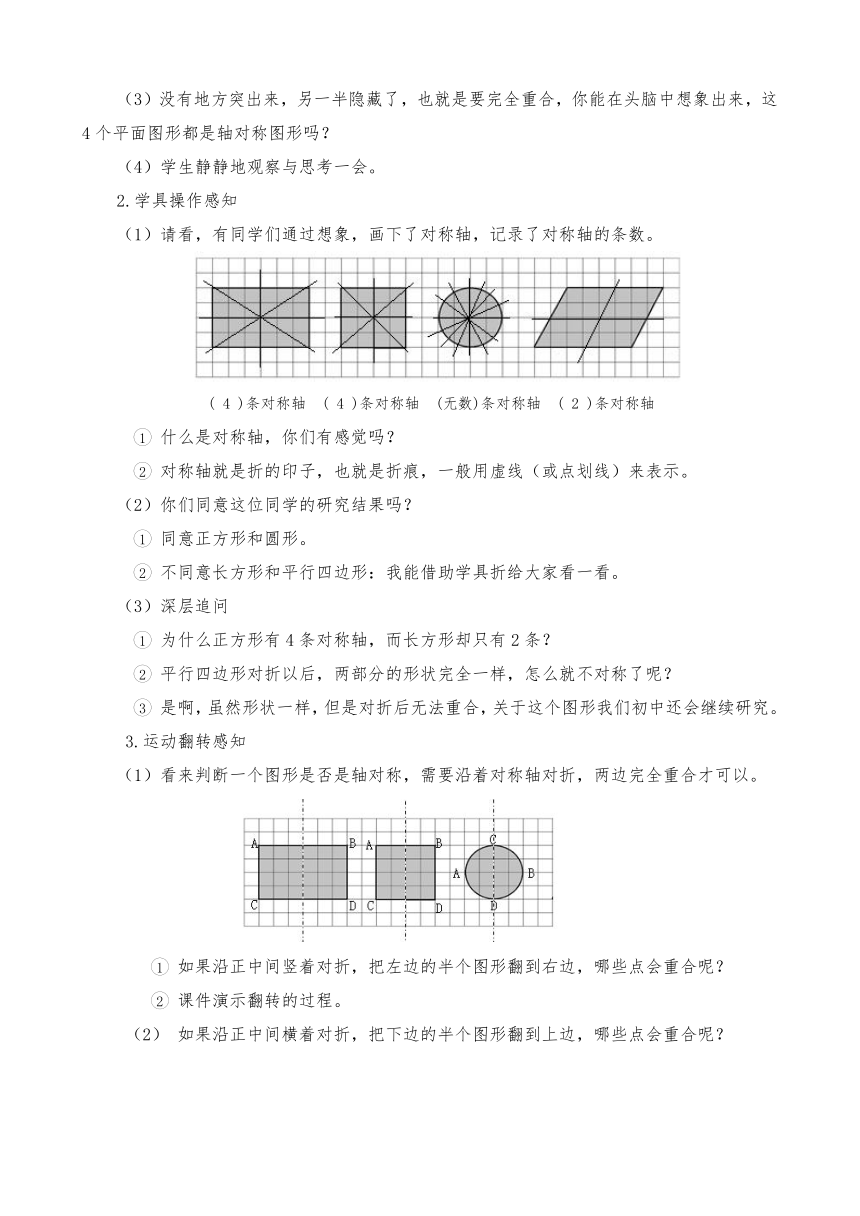
(1)请看,有同学们通过想象,画下了对称轴,记录了对称轴的条数。
( 4 )条对称轴 ( 4 )条对称轴 (无数)条对称轴 ( 2 )条对称轴
什么是对称轴,你们有感觉吗?
对称轴就是折的印子,也就是折痕,一般用虚线(或点划线)来表示。
(2)你们同意这位同学的研究结果吗?
同意正方形和圆形。
不同意长方形和平行四边形:我能借助学具折给大家看一看。
(3)深层追问
为什么正方形有4条对称轴,而长方形却只有2条?
平行四边形对折以后,两部分的形状完全一样,怎么就不对称了呢?
是啊,虽然形状一样,但是对折后无法重合,关于这个图形我们初中还会继续研究。
3.运动翻转感知
(1)看来判断一个图形是否是轴对称,需要沿着对称轴对折,两边完全重合才可以。
如果沿正中间竖着对折,把左边的半个图形翻到右边,哪些点会重合呢?
课件演示翻转的过程。
如果沿正中间横着对折,把下边的半个图形翻到上边,哪些点会重合呢?
课件演示翻转的过程。
② 除了标注的点以外,你还能找到其他重合的地方吗?(重合的点、线、面)
(3)正方形和圆形还可以这样斜着对折(演示翻转过程),会重合的点你还能找到吗?
思考:圆形还可以继续对折下去,图形在对折过程中,什么没变,什么变了?
4.小结求同:现在你会判断,怎样的图形是对称图形了吗?对折后,一半图形翻转到另一边,一半和另一半完全重合。翻折过程中,虽然样子没有变,但是朝的方向却变了。
【解读:《标准》指出空间观念主要指对图形形状、大小及位置关系的感悟,感知并描述图形运动和变化的规律。此处通过“想—折—看”三个活动,让学生完整经历“如何判断一个图形是否是对称图形”的整个过程。首先,需要教师创设机会给学生空间想象的机会,不断形成空间想象力的经验基础;其次,对于空间想象上遇到困难的学生,可以借助动手操作加以验证,降低空间想象的难度;最后,通过课件演示找重合的点、线、面,让学生感受图形翻转的过程及特点,体会运动前后图形的变与不变,逐步形成空间观念,增强几何直观。此外,在选取研究素材时,平行四边形是一个比较特殊的材料,虽然没有轴对称,但是它属于中心对称图形,结构性材料为今后初中的教学埋下伏笔。】
三、思维提升与拓展,感受轴对称的结构美
1.同学们现在会判断怎样的图形是对称图形了吗?我们一起来试一试。
(1)①号三角形对称吗?你是怎么判断的?
上面的边有6格长,左边的边只有5格长,翻转对折后无法重合,所以不对称。
(2)之前讨论的平行四边形不是轴对称图形,这个②号平行四边形怎么又是轴对称图形了?
它有几条对称轴?会不会也像正方形一样,也有4条呢?
2.挑战:③号梯形是不对称的,大家没有异议。如果让它通过“翻转对折”也变成轴对称图形,你能画出它的另一半吗?看看你能想到多少种不同的方法?
学生独立尝试。
整体反馈与交流。
这些画法你们都同意吗?你们是怎么画出来的?
对称中关键的点你们是怎么找到的?
怎样才能保证对折后和原来的图形完全重合?
想象后课件演示翻转运动的过程:请你想象一下,这些图形沿着对称轴对折,两边能完全重合吗?
为什么你们都不选择以梯形的最后一条边为对称轴呢?
能想象出对称的另一半长什么样吗?难画并不代表不存在(课件演示翻转),是这样吗?像一个爱心的形状,是不是感觉很神奇呢?
3. 总结与实践
(1)回顾这节课,大家有什么收获?
(2)轴对称的现象生活中随处可见,课后大家想不想利用手中的彩纸创作一些美丽的轴对称图案呢 到时我们一起来展示与分享。
【解读:《标准》指出通过数学课程的学习,使学生养成数学学习的兴趣、好奇心和求知欲。所以作为数学教师,不仅仅满足于让学生获得结论性的知识,而应努力让他们在思维上有提升与拓展,帮他们开启疑惑、思维之门。
让轴对称图形“运动”起来,才能促进学生空间观念的发展,真正实现从运动变换的视角去研究几何图形的目的,此处依托开放的学习素材展开,为学生回顾和提升本节课所学内容做好铺垫。具体从以下三个活动推进,活动一:判断平面图形是否是轴对称图形,尤其是特殊的平行四边形又是轴对称图形了,是对前面环节做的一次爬升,打破思维定势;活动二:不是轴对称图形,你能通过翻折运动“补出另一半图形”吗?在方法展示和深层追问中,学生对“怎么找出另一半”和“怎样保证对折后和原来的图形完全重合”两个问题越来越清晰,逐渐感悟到了“图形关于不同方向直线的翻折,创造出的轴对称图形是不同的”,对称位置不同,对应点的位置也不一样;活动三:学生课后的设计创作活动,学生只要对折后采用绘、剪、撕等方法都能创作出具有对称特点的图案,实践性作业能让学生乐学其中。】
【案例简介】
内容分析:
“轴对称”是图形与几何领域典型的内容,属于“图形的位置与运动”版块,内容安排在第二学段(3-4年级),它不是静态的图形认识,与平移、旋转、缩放一起构成了图形运动的四种基本方式,所以突出运动和变化是轴对称教学的核心与关键,应是教学的深层追求。在第一学段(1-2年级)中,学生已经会辨认常见的平面图形,能直观描述图形的特征,对轴对称现象已有一定的认识基础,同时此处学习也为第三学段(5-6年级)利用四种基本变换设计图案奠定基础,更为第四学段(7-9年级)学习中心对称图形埋下伏笔,承前启后,具有一定的连续性和整体性。
教学目标:
1.通过观察和操作,认识对称现象和轴对称变换,并学会找对称轴。
2.能根据轴对称图形的特征,鼓励学生用多种方法验证对称图案,重点借助“翻折运动”培养学生的观察能力、动手能力、想象能力。
3.能利用轴对称的特点,在方格纸上补全简单的轴对称图形,在思维拓展中促进学生空间观念的发展。
4.感受物体或图形的对称美,体会学习数学的乐趣。
教学过程:
创设生活情境,初步感知轴对称;经历活动的过程,多角度感知图形的对称变换;思维提升与拓展,感受轴对称的结构美。
【标准要求】
内容要求:
认识轴对称图形和对称轴,能在方格纸上补全简单的轴对称图形;在感受图形位置与运动的过程中,增强空间观念和几何直观。
学业要求:
能认识现实生活中的轴对称图形,知道轴对称图形对称轴的数量,能在方格纸上补全轴对称图形。
教学提示:
图形运动的教学,可以通过有趣的活动或者长作业的方式,帮助学生感知轴对称的特征,增强对轴对称的理解,以增强学生的空间观念,帮助学生积累有计划、有条理做事的实践经验。
【案例解读】
一.创设生活情境,初步感知轴对称
(一)感知对称现象
1.同学们,这是什么?(逐个呈现:脸谱、树叶、剪纸、蝴蝶、天安门,引导学生依次回答名称。)它们有什么共同的特点呢?
2.脸谱、天安门、树叶、蝴蝶左右一样,剪纸上下一样,它们都是对称的。
(二)揭示课题
像这样两边都一样的现象我们称为“对称”现象,对称现象在生活中随处可见,我们把它们画下来就得到了“轴对称图形”,今天我们就来研究对称现象中的“轴对称图形”。
【解读:《标准》在教学提示中提出,图形运动的教学可以从有趣的活动入手,本案例中从学生熟悉生活场景中的对称现象直接导入新课,引导学生通过观察,初步感受一半和另一半一样的现象,初步了解什么是对称,感知对称现象在生活中无处不在。同时,对称现象与轴对称图形具有本质的区别,所以在揭示课题处有意识从“现象”过渡到“平面图形”,避免两者混为一谈。】
二、经历活动的过程,多角度感知图形的对称变换
(一)大任务驱动
1.下面的平面图形相信你都认识,平面图形中有些也是对称的,你能找到吗? 如果是对称图形,各有几条对称轴呢?试着把他们画出来。
( )条对称轴 ( )条对称轴 ( )条对称轴 ( )条对称轴
2.你打算怎么研究?请拿出学习材料单。
(二)汇报交流:你觉得哪些是对称的?你是怎么想的?
1.初步想象感知
(1)想一想,怎样判断一个图形是轴对称图形呢?
(2)有同学们建议可以在头脑中想象对折的操作,一个图形是不是只要对折就能判断了呢?
(3)没有地方突出来,另一半隐藏了,也就是要完全重合,你能在头脑中想象出来,这4个平面图形都是轴对称图形吗?
(4)学生静静地观察与思考一会。
2.学具操作感知
(1)请看,有同学们通过想象,画下了对称轴,记录了对称轴的条数。
( 4 )条对称轴 ( 4 )条对称轴 (无数)条对称轴 ( 2 )条对称轴
什么是对称轴,你们有感觉吗?
对称轴就是折的印子,也就是折痕,一般用虚线(或点划线)来表示。
(2)你们同意这位同学的研究结果吗?
同意正方形和圆形。
不同意长方形和平行四边形:我能借助学具折给大家看一看。
(3)深层追问
为什么正方形有4条对称轴,而长方形却只有2条?
平行四边形对折以后,两部分的形状完全一样,怎么就不对称了呢?
是啊,虽然形状一样,但是对折后无法重合,关于这个图形我们初中还会继续研究。
3.运动翻转感知
(1)看来判断一个图形是否是轴对称,需要沿着对称轴对折,两边完全重合才可以。
如果沿正中间竖着对折,把左边的半个图形翻到右边,哪些点会重合呢?
课件演示翻转的过程。
如果沿正中间横着对折,把下边的半个图形翻到上边,哪些点会重合呢?
课件演示翻转的过程。
② 除了标注的点以外,你还能找到其他重合的地方吗?(重合的点、线、面)
(3)正方形和圆形还可以这样斜着对折(演示翻转过程),会重合的点你还能找到吗?
思考:圆形还可以继续对折下去,图形在对折过程中,什么没变,什么变了?
4.小结求同:现在你会判断,怎样的图形是对称图形了吗?对折后,一半图形翻转到另一边,一半和另一半完全重合。翻折过程中,虽然样子没有变,但是朝的方向却变了。
【解读:《标准》指出空间观念主要指对图形形状、大小及位置关系的感悟,感知并描述图形运动和变化的规律。此处通过“想—折—看”三个活动,让学生完整经历“如何判断一个图形是否是对称图形”的整个过程。首先,需要教师创设机会给学生空间想象的机会,不断形成空间想象力的经验基础;其次,对于空间想象上遇到困难的学生,可以借助动手操作加以验证,降低空间想象的难度;最后,通过课件演示找重合的点、线、面,让学生感受图形翻转的过程及特点,体会运动前后图形的变与不变,逐步形成空间观念,增强几何直观。此外,在选取研究素材时,平行四边形是一个比较特殊的材料,虽然没有轴对称,但是它属于中心对称图形,结构性材料为今后初中的教学埋下伏笔。】
三、思维提升与拓展,感受轴对称的结构美
1.同学们现在会判断怎样的图形是对称图形了吗?我们一起来试一试。
(1)①号三角形对称吗?你是怎么判断的?
上面的边有6格长,左边的边只有5格长,翻转对折后无法重合,所以不对称。
(2)之前讨论的平行四边形不是轴对称图形,这个②号平行四边形怎么又是轴对称图形了?
它有几条对称轴?会不会也像正方形一样,也有4条呢?
2.挑战:③号梯形是不对称的,大家没有异议。如果让它通过“翻转对折”也变成轴对称图形,你能画出它的另一半吗?看看你能想到多少种不同的方法?
学生独立尝试。
整体反馈与交流。
这些画法你们都同意吗?你们是怎么画出来的?
对称中关键的点你们是怎么找到的?
怎样才能保证对折后和原来的图形完全重合?
想象后课件演示翻转运动的过程:请你想象一下,这些图形沿着对称轴对折,两边能完全重合吗?
为什么你们都不选择以梯形的最后一条边为对称轴呢?
能想象出对称的另一半长什么样吗?难画并不代表不存在(课件演示翻转),是这样吗?像一个爱心的形状,是不是感觉很神奇呢?
3. 总结与实践
(1)回顾这节课,大家有什么收获?
(2)轴对称的现象生活中随处可见,课后大家想不想利用手中的彩纸创作一些美丽的轴对称图案呢 到时我们一起来展示与分享。
【解读:《标准》指出通过数学课程的学习,使学生养成数学学习的兴趣、好奇心和求知欲。所以作为数学教师,不仅仅满足于让学生获得结论性的知识,而应努力让他们在思维上有提升与拓展,帮他们开启疑惑、思维之门。
让轴对称图形“运动”起来,才能促进学生空间观念的发展,真正实现从运动变换的视角去研究几何图形的目的,此处依托开放的学习素材展开,为学生回顾和提升本节课所学内容做好铺垫。具体从以下三个活动推进,活动一:判断平面图形是否是轴对称图形,尤其是特殊的平行四边形又是轴对称图形了,是对前面环节做的一次爬升,打破思维定势;活动二:不是轴对称图形,你能通过翻折运动“补出另一半图形”吗?在方法展示和深层追问中,学生对“怎么找出另一半”和“怎样保证对折后和原来的图形完全重合”两个问题越来越清晰,逐渐感悟到了“图形关于不同方向直线的翻折,创造出的轴对称图形是不同的”,对称位置不同,对应点的位置也不一样;活动三:学生课后的设计创作活动,学生只要对折后采用绘、剪、撕等方法都能创作出具有对称特点的图案,实践性作业能让学生乐学其中。】
